江苏省高邮中学2006~2007年度下学期高三一模拟测试
数学试卷2007.03.29
参考公式：
如果事件A在一次实验中发生的概率是P，那么n次独立重复实验中恰好发生k次的概率：
Pn(k)=Cnk.Pk.(1-P)n-k
球的体积公式V=
R3 （其中R表示球的半径）
一组数据
的方差
一、选择题（本大题翻工10小题，每小题5分，共50分。在每小题给出的四个选项中，只有一项是符合题目要求的）
1. 设A-B={x︱x∈A且x
B }.若M={4,5,6,7,8},N={7,8,9,10},则M-N等于
A. {4,5,6,7,8,9,10} B. {7,8} C. {4,5,6,9,10} D. {4,5,6}
2. 将函数
的图象按向量
平移后所得函数图象的解析式是
A.
B. 
C.
D. 
3. 下列命题中正确的是
A若
,且
,则 
B 若
且
则
C 若且
,则
D 若
则
4. 若数列
是等差数列,
,则
等于
A. 24 B. 25 C. 26 D 27
5. 已知
,
是第二象限角,且
,则
的值为
A . 2 B. 3 C . -3 D -2
6. 设
, 则“
”是“曲线
为双曲线”的
A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件
7.在四棱锥P-ABCD中,底面ABCD是边长为
的菱形,AC与BD交于O,PO⊥平面
ABCD,PA=
,则PB长度的取值范围为
A.
B.
C.
D.
8.某企业要从其下属6个工厂中抽调8名工程技术人员组成课题攻关小组,每厂至少调1人,则这8个名额的分配方案共有( ) A.21种 B.15种 C.36种 D.30种
9. 对于任意的x∈R, 不等式 2x2－a＋3>0恒成立, 则实数a 的取值范围是( )
A. a<2 B. a≤2 C. a<3 D. a≤3
10. 对于函数
,若将满足
的实数
叫做函数的零点,则函数
的零点有 ( ) A .0 个 B. 1个 C .2个 D. 3个
二、填空题：本大题共6小题，每小题5分，共30分.把答案填在涂中横线上.
| |
的展开式中x2的系数与
的展开式中x3的二项式系数相等，则cosθ= .
12．若关于x的不等式
.
13．在军训期间，某校学生进行实弹射击．通过抽签，将编号为1~6的六名同学排到1~6号靶位，则恰有3名同学所抽靶位号与其编号相同的概率
14．函数
的最大值为
.
15.定义在R上的函数y=f(x)满足: f(－x)=－f(x), f(1＋x)=f(1－x), 当x∈[－1,1]时, f(x)=x3,则f(2007)的值是
16 设
为椭圆
的焦点,过
且垂直于轴的直线与椭圆交于A,B两点,若△
为锐角三角形,则该椭圆离心率
的取值范围是
.
三、解答题“本大题共5小题，共70分.解答应写出文字说明，证明过程或演算步骤.
17. 已知
，(1)求
；
(2)设
，且已知
，求
。
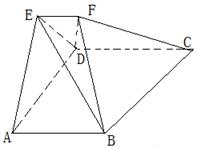
18. 在多面体ABCDEF中，△ADE是边长为2的等边三角形，EF∥平面ABCD，AB⊥平面ADE，AB=
，EF=
.（1）求证AB∥DC；（2）求直线BE与平面ABCD所成的角；
（3）若DF⊥FC，求证DF⊥BC.
19. 已知动点M到点F
.（1）求动点M的轨迹C的方程；（2）若过点E（0，1）的直线与曲线C在y轴左侧交于不同的两点A、B，点P（－2，0）满足
，求直线PN在y轴上的截距d的取值范围.
20.
21. 已知函数
对任意的实数
都有
.
（Ⅰ）记
为等比数列，求
的值.
（Ⅱ）在（Ⅰ）的条件下，设
问：是否存在最大的整数
，使
得对于任意
均有
？若存在，求出的值；若不存在，请说明理由.
07届高邮中学高三迎一模适应考试数学试卷答案:
1-10 1．D 2．A 3．C 4．B 5．C 6．C 7．D 8．A 9．C 10．C
11．
12．－2 13． 14．
15．-1；
16．
17. 解：(1)由已知，
即
，
所以
，由余弦定理,
；
(2)由(1)，
，所以
如果
则
，所以
此时
。
19. 解：（1）设动点M的坐标为（x，y），由题设可知
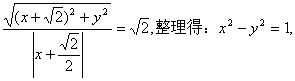∴动点M的轨迹C方程为
（2）设A（x1，y1），B（x2，y2），由题设直线AB的方程为：
由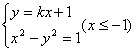
消去y得：
由题意可得：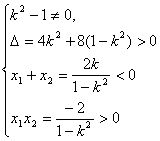
解得
……………（8分）
则
…（10分）
令
上为减函数.
………………（12分）
18.
21. 解：（Ⅰ）
对于任意的
均成立，
是以为首项，为公比的等比数列，
…………（2分）
当
不是等比数列，
……（3分）
成等比数列，
成等比数列，
,
解得
（8分）
（Ⅱ）在（Ⅰ）的条件下，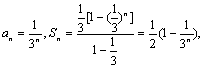
…………（9分）
由
………（12分）
且当
时，均有
存在这样的
能使对所有的
有成立.…………（14分）
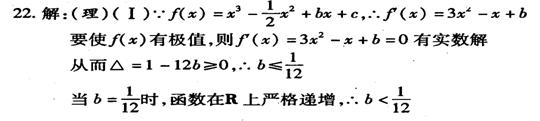
20.
