|
数学（理）试题
本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，满分150分，考试时间120分钟。
第Ⅰ卷（选择题 共60分）
一、选择题（本题共12小题，每小题5分，共60分.在每小题给出的四个选项中，有且只有一个是正确的）
1．如果复数z满足：z2+1=0，则
（
为虚数单位）的值为 （ ）
A．± B．－ C．±1 D．1
2．已知随机变量ξ~N（3，22），若ξ=2η+3，则Dη= （ ）
A．0 B．1 C．2 D．4
3．已知{an}是正项的等差数列，如果满足
则数列{an}的前11项的和为 （ ）
A．8 B．44 C．56 D．64
4．函数
的值域是 （ ）
A．
B．
C．
D．
5．设a，b∈R，则“a+b=1”是“4ab≤1”的（ ）条件
A．充分非必要 B．必要非充分
C．充分条件 D．既不充分也不必要条件
6．函数
在R上存在极值点，则实数a的取值范围是 （ ）
A．
B．
C．
D．
7．设m、n都是不大于6的自然数，则方程
表示双曲线的个数是（ ）
A．16 B．15 C．12 D．6
8．已知平面向量
两两所成的角相等，则
= （ ）
A．
B．6或
C．6 D．6或
9．双曲线
的左焦点为F1，顶点为A1，A2，P是该双曲线右支上任意一点，则分别以线段PF1，A1A2为直径的两圆一定 （ ）
A．相交 B．内切 C．外切 D．相离
|
A．0 B．2 C．4 D．4个以上
|
12．在△ABC中，角A、B、C所对的边分别是
，若△ABC最长的边为1，则最短边的长为 （ ）
A．
B．
C．
D．
第Ⅱ卷（非选择题 共60分）
二、填空题（每小题4分，共16分把答案填在答题卷中横线上）
13．若x＞1，不等式
恒成立，则实数k的取值范围是
。
14．已知二项式
的展开式中含x3的项是第4项，则n的值为
。
15．在长方体ABCD—A1B1C1D中，AB=2，AA1=AD=1，点E、F、G分别是棱AA1、C1D1与BC的中点，那么四面体B1—EFG的体积是 .
|
①过一点与已知曲线相切的直线有用只有一条；②函数
对称中心是（－
，－），③已知Sn是等差数列{an}(n∈N*)的前n项和，若S7>S5，则S9>S3；④函数f(x)=xx+px+q(x∈R)为奇函数的充要条件是q=0；⑤已知a，b，m均是正数，且a<b，则
.其中真命题的序号是 （将所有真命题的序号都填上）。
三、解答题（本大题共6小题，共74分。解答应写出文字说明，证明过程或演算步骤。）
17．（本小题满分12分）
在△ABC中，设
（1）求证：△ABC为等腰三角形；
（2）若
的取值范围。
18．（本题满分12分）
已知函数
（1）若f（x）在
上是增函数，求实数a的取值范围；
（2）若x=3是f（x）的极值点，求f（x）在
上的最小值和最大值.
19．（本小题满分12分）
|
，点E在PD上，且PE：ED=2：1
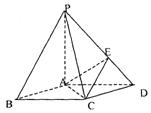
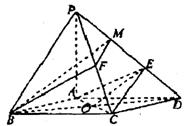
（1）证明PA⊥平面ABCD
（2）求以AC为棱， EAC与DAC为面的二面角θ的大小；
（3）在棱PC上是否存在一点F，使BE//平面AEC？证明你的结论。
20．（本小题满分12分）
骰子是一个质量均匀的正方体，6个面上分别刻有1、2、3、4、5、6点。现在桌面上有3只骰子分别为木制、骨制、塑料制的。重复下面操作，直到桌子上没有骰子：将桌上的骰子全部掷出，然后去掉那些奇数点的骰子。
（1）求完成以上操作的次数是二次的概率；
（2）求完成以上操作的次数多于三次的概率。
21．（本小题满分12分）
已知椭圆
的左、右焦点分别为F1，F2，右顶点为A，P是椭圆C1上任意一点，设该双曲线C2：以椭圆C1的焦点为顶点，顶点为焦点，B是双曲线C2在第一象限内的任意一点，且
（1）设
，求椭圆离心率；
（2）若椭圆离心率
成立.
22．（本小题满分14分）
设数列{an}的各项都是正数，且对任意n∈N+，都有
，记Sn为数列{an}的前n项和.
（1）求证：
=2Sn－an；
（2）求数列{an}的通项公式；
（3）若
（
为非零常数，n∈N+），问是否存在整数，使得对任意 n∈N+，都有bn+1>bn.
|
数学（理）试题参考答案
一、选择题（每小题5，共60分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | C | B | B | A | A | D | A | D | B | A | D | A |
|
13．
14．9 15．
16．③④⑤
三、解答题
17．（1）因为
，
所以
即AB=BC，故△ABC为等腰三角形。（6分）
（2）因为
，
（12分）
18．解：（I）
上是增函数，则有
又
（当且仅当x=1时取等号），所以a≤3（6分）
（II）由题意知
=3x2－2ax+3=0的一个根为x=3，可得a=5，
所以=3x2－10x+3=0的根为x=3或x=
（舍去），又f(1)=－1，
f(3)=－9,f(5)=15，∴f(x)在x∈[1，5]上的最小值是f(3)=－9，最大值是f(5)=15
19．证明：因为底面ABCD是菱形，∠ABC=60°，所以AB=AD=AC=a，在△PAB中，
由PA2+AB2=2a2=PB2 知PA⊥AB.
|
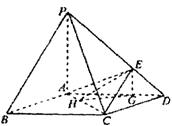
（II）解 作EG//PA交AD于G，
由PA⊥平面ABCD.
知EG⊥平面ABCD.作GH⊥AC于H，连结EH，
则EH⊥AC，∠EHG即为二面角θ的平面角.
又PE：ED=2：1，
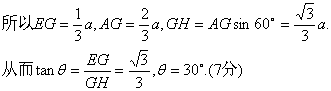
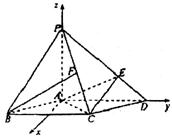
（III）解法一 以A为坐标原点，直线AD、AP分别为y轴、z轴，过A点垂直平面PAD的直线为x轴，建立空间直角坐标系如图.由题设条件，相关各点的坐标分别为
A（0，0，0），B（
a，－a，0），C（a， a，0）.
|
.
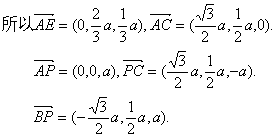
设点F是棱PC上的点，
，则
|
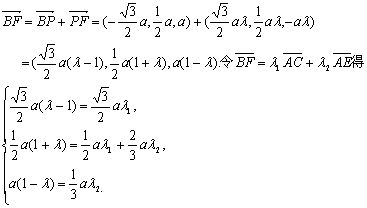
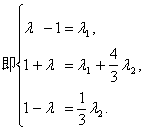
亦即，F是PC的中点时，
、
、
共面.
又BF
平面AEC，所以当F是棱PC的中点时，BF//平面AEC.（12分）
解法二 当F是棱PC的中点时，BF//平面AEC，证明如下，
证法一 取PE的中点M，连结FM，则FM//CE.①
由
，知E是MD的中点.
连结BM、BD，设BD∩AC=O，则O为BD的中点.
所以BM//OE. ②
由①、②知，平面BFM//平面AEC 。
又BF
平面BFM，所以BF//平面AEC.
证法二：
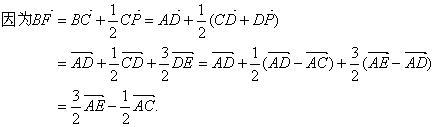
所以、、共面.
又BF平面ABC，从而BF//平面AEC.
20．（1）
（4分）
（2）操作次数为一次的概率P1=
（6分）
操作次数为三次的概率：
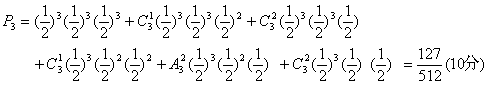
所以操作三次以上的概率为
（12分）
21．（1）设P（x，y），又F1（－c，0），F2（c，0）∴
，
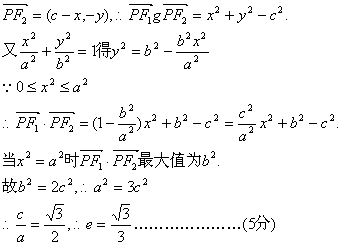
（2）由椭圆离心率
得双曲线
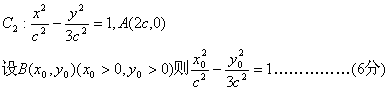
①当AB⊥x轴时，x0=2c,y0=3c.
∴tan∠BF1A=1, ∴∠BF1A=45°∴∠BAF1=
=2∠BF1A…………（7分）
②当x≠2c时.
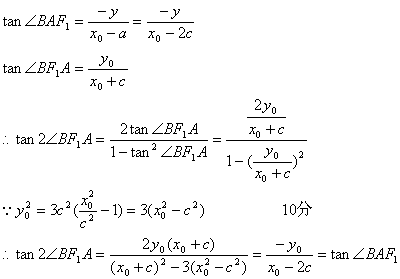
又2∠BF1A与∠BAF1同在
内
2∠BF1A=∠BAF1
总2∠BF1A=∠BAF1有成立。……………………………………（12分）.
22．解：（1）在已知式中，当n=1时，
∵a1>0 ∴a1=1……………………………………1分
当n≥2时， ①
②
①－②得，
…………………………3分
∵an>0 ∴=2a1+2a2+…+2an－1+an，
即=2Sn－an ∵a1=1适合上式
∴=2Sn－an(n∈N+)……………………5分
（2）由（1）知=2Sn－an(∈N+) ③
当n≥2时， 
=2Sn－1－an－1
④
③－④得－=2(Sn－Sn－1)－an+an－1=2an－an+ an－1= an+
an－1
∵an+an－1>0 ∴an－an－1=1……………………8分
∴数列{an}是等差数列，首项为1，公差为1，可得an=n………………9分
（3）∵
∴
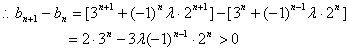
⑤……………………11分
当n=2k－1，k=1，2，3，……时，⑤式即为
⑥
依题意，⑥式对k=1，2，3……都成立，∴λ<1………………12分
当n=2k，k=1，2，3，…时，⑤式即为
⑦
依题意，⑦式对k=1，2，3，……都成立，
∴
……………………13分
∴
∴存在整数λ=－1，使得对任意n∈N，都有bn+1>bn………………14分