云 南 省2007年第一次高中毕业生复习统一检测
数学试题（理科）
本试卷分第I卷（选择题）和第II卷（非选择题）两部分. 满分150分，考试用时120分钟。
注意事项：
1．答题前，考生务必用黑氏以碳素笔将自己的姓名、准考证号、考场号、座位号在答题卡上填写清楚，并认真核准条形码上的准考证号、姓名及科目，在规定的位置贴好条形码。
2．每小题选出答案后，用2B氏风吹草动笔把答题卡上对应题目的答案标号涂黑. 如需改动，用橡皮擦干净后，再选涂其它答案标号. 答在试卷上的答案无效.
参考公式：
如果事件A、B互斥，那么 球的表面积公式
P(A+B)=P(A)+P(B)
如果事件A、B相互独立，那么
P(A·B)=P(A)·P(B) 其中R表示球的半径
如果事件A在一次试验中发生的概率是 球的体积公式
P，那么n次独立重复试验中恰好发生k
第I卷（选择题，共60分）
一、选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.
1．如果复数
为纯虚数，那么实数a的值为 （ ）
A．
B．0 C．2 D．8
2．在边长等于1的正三角形ABC中，设
等于 （ ）
A．
B．－ C．
D．－
3．已知方程
的两个实数根是tanα、tanβ，且
、
，则
α+β= （ ）
A．
B．－ C．
D．
4．已知
，那么 （ ）
A．
B．
C．
D．
5．等差数列{
}的前n项和为
，若
等于 （ ）
A．
B．
C．
D．
6．一个长方体的八个顶点都在球O的面上，如果经过该长方体同一个顶点的三个面的面对角线的长分别为7、8、9，那么球O的表面积等于 （ ）
| |
7．已知点F1、F2分别是椭圆
的左、右焦点，点P在此椭圆上，则△PF1F2的周长等于 （ ）
A．20 B．18 C．16 D．14
8．函数
（ ）
A．既不是奇函数也不是偶函数 B．既是奇函数又是偶函数
C．是偶函数但不是奇函数 D．是奇函数但不是偶函数
9．如果
等于 （ ）
A．2 B． C．1 D．3
10．椭圆
和圆
的位置关系是 （ ）
A．相离 B．相切 C．相交 D．无法确定
11．已知m是正整数，则
等于 （ ）
A．m B．m－1 C．1 D．0
12．函数
、
在区间
上满足
，则对任意
都有 （ ）
A．
B．
C．
D．
第II卷（非选择题，共90分）
二、填空题：本大题共4小题，每小题4分，共16分.把答案直接填在答题卡上.
13．抛物线
的准线方程是
.
14．某学校共有6个年级，现在采用分层抽样的方法从全校3000名学生中抽取一个容量为150的样本进行一项调查. 若该学校高中三年级共有600名学生，则从高中三年级抽取的学生人数应该为 .
15．已知
，则AB的最小值为
.
|
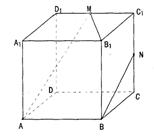
①直线AM与CC1是相交直线；
②直线AM与BN是平行直线；
③直线BN与MB1是异面直线；
④直线AM与DD1是异面直线；
其中正确的结论为 （注：
把你认为正确的结论的序号都填上）.
| |
17．（本小题满分12分）
已知A、B、C三个点在同一个平面直角坐标系中的坐标分别为A（4，0），B（0，4），
（I）若
，求角α的值；
（II）若
.
18．（本小题满分12分）
从6名男同学和4名女同学中随机选出3名同学参加一项测试，每位同学通过测试的概率都为
试求
（I）选出的三位同学中，至少有一名女同学的概率；
（II）选出的三位同学中，同学甲被选中并且通过测试的概率；
（III）设选出的三位同学中男同学的人数为ξ，求ξ的分布列和数学期望.
19．（本小题满分14分）
|
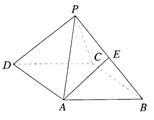
（I）求侧面PAD与底面ABCD所成的二面角的大小；
（II）求异面直线PD与AE所成角的正切值；
（III）在侧面PAD上寻找一点F，使EF⊥侧面PBC，
试确定点F的位置，并证明你找出的点F满足EF⊥侧面PBC.
20．（本小题满分12分）
已知是数列{}的前n项和，并且
=1，对任意正整数n，
；设
）.
（I）证明数列
是等比数列，并求的通项公式；
（II）设
的前n项和，求
.
21．（本小题满分14分）
已知函数
上是增函数，在区间（0，2）上是减函数，并且方程
有三个实数根，它们分别为α、2、β.
（I）求c的值；
（II）求证：f（1）≥2；
（III）求α－β的取值范围.
22．（本小题满分12分）
无论m为任何实数，直线
恒有公共点.
（I）求双曲线C的离心率e的取值范围；
（II）若直线l经过双曲线C的右焦点F与双曲线C交于P、Q两点，并且满足
，求双曲线C的方程.
云 南 省2007年第一次高中毕业生复习统一检测
数学试题（理科）
参考答案
一、选择题：本大题共12小题，每小题5分，共60分.
1—5：DBBCB 6—10：ABDAC 11—12：AC
二、填空题：本大题共4小题，每小题4分，共16分.
13．
14．30 15．3 16．③、④
三、解答题： 本大题共6小题，共74分.
17．（本小题满分12分）
解：（I）
，
，
……………………………………………………………………4分
又
，
……………………………………………………………………6分
（II）
，
化简得
……………………………………………………9分
两边平方：
，
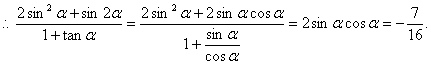
………………………………………………12分
18．（本小题满分12分）
解：（I）
…………………………………………………………4分
（II）甲被选中的概率为
，
∴甲被选中且通过测试的概率为
………………………………8分
（III）ξ的取值为0、1、2、3，
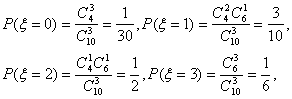
∴ξ的分布列为：
| ξ | 0 | 1 | 2 | 3 |
P |
|
|
|
|
∴Eξ=+1+=
………………………………………………………………12分
19．（本小题满分12分）
方法一：
|
，
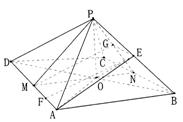
由已知得PO⊥平面ABCD，AO=
（I）取AD的中点M，连接MO、PM，
根据已知可得∠PMO为侧面PAD与
底面ABCD所成的二面角的平面角，…………2分
∠PAO为侧棱PA与底面ABCD所成的角，
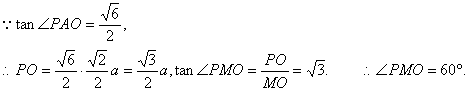
∴侧面PAD与底面ABCD所成的二面角的大小为60°.…………………………4分
（II）连结OE，OE∥PD，
∴∠OEA为异面直线PD与AE所成的角，………………………………………6分
而OE=PD=
∴异面直线PD与AE所成角的正切值为
.………………………………8分
（III）F在线段AD上，且AF=
AD.……………………………………………9分
延长MO交BC于N，取PN的中点G，连结EG、MG，
⊥平面PMN，
∴平面PMN⊥平面PBC，
为正三角形，∴MG⊥PN，
∵平面PMN∩平面PBC=PN，
∴MG⊥平面PBC，∵EG∥MF，∴MF=MA=EG，
∴EF∥MG，∴EF⊥平面PBC.……………………………………………………12分
|
，
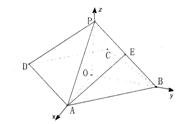
以射线OA、OB、OP分别为x轴、y轴、z轴正半轴，
如图建立空间直角坐标系，根据已知，
故A（
（I）可以求得底面ABCD的一个法向量
，
侧面PAD一个法向量
，
根据已知：侧面PAD与底面ABCD所成的二面角为锐角，设为
，则
，
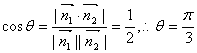即侧面PAD与底面ABCD所成的二面角的大小为
.…………………………4分
（II）由已知得：
设PD与AE所成角为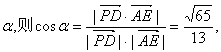
即异面直线PD与AE所成角的正切值为.………………8分
（III）F在线段AD上，且AF=AD.……………………………………………9分
设
根据已知：P、A、F、D共面，即
，
∴F在线段AD上，且AF=AD.……………………………………………………12分
20．（本小题满分12分）
解：（I）
两式相减：
是以2为公比的等比数列，…………………………………………4分
…………………………………………………………7分
（II）
……………………9分
而
……………12分
21．（本小题满分14分）
（I）解：
上是增函数，在区间（0，2）上是减函数，
∴当x=0时，取极大值，
，
∴c=0.…………………………………………………………………………………4分
（II）证明：
令
在区间（0，2）上是减函数，
…………………………8分
（III）解：=0的三个实根为α、0、β，故设
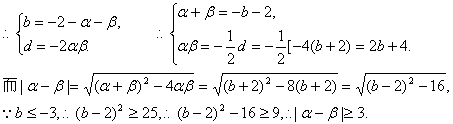
的取值范围为
……………………………………………………14分
22．（本小题满分12分）
解：（I）把
，
整理得：
当b2=2，m=0时直线与双曲线无交点，这和直线与双曲线恒有公共点矛盾，
∴b2≠2，
.
当b2≠2时，直线与双曲线恒有公共点
恒成立，
即
恒成立，……………………………………………………2分
，
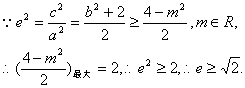
综上所述，
……………………………………………………………6分
（II）设F（c，0），则
代入双曲线方程中得：
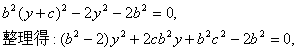
设两交点为
，
…………………………………………………………9分
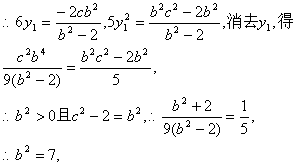
∴所求双曲线C的方程为
…………………………………………12分
请注意：以上参考答案与评分标准仅供阅卷时参考，其他答案请参考评分标准酌情给分.