江苏省姜堰中学数学综合练习(四)2007.4
班级 学号 姓名
一、选择题(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.已知集合![]() ,
,![]() ,则
,则![]() 、
、![]() 的关系为 ( )
的关系为 ( )
A.![]() B.
B.![]()
![]() C.
C.![]()
![]() D.
D.![]()
2.从8名女生,4名男生中选出6名学生组成课外小组,如果按性别比例分层抽样,则不同的抽取方法种数为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.已知△ABC中,![]() 等于
( )
等于
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.已知f(x)=![]() ,则f(3)=
( )
,则f(3)=
( )
A.1 B.2 C.3 D.4
5.已知向量![]() ( )
( )
A.30° B.60° C.120° D.150°
6.![]() 与
与![]() 是两个不同的平面,对下列条件:①存在平面
是两个不同的平面,对下列条件:①存在平面![]() ,使得
,使得![]() 、
、![]() 都垂直于
都垂直于![]() ;②存在
;②存在
平面![]() ,使得
,使得![]() 、
、![]() 都平行于
都平行于![]() ;③
;③![]() 内有不共线的三点到
内有不共线的三点到![]() 的距离相等;④存在异面直线l、m,使得l//
的距离相等;④存在异面直线l、m,使得l//![]() ,l//
,l//![]() ,m//
,m//![]() ,m//
,m//![]() ,其中可以判定
,其中可以判定![]() 与
与![]() 平行的条件有( )
平行的条件有( )
A.1个 B.2个 C.3个 D.4个
7.若x,y是正数,则![]() 的最小值是
( )
的最小值是
( )
A.3 B.![]() C.4 D.
C.4 D.![]()
8.设k>1,f(x)=k(x-1)(x∈R),在直角坐标系中,函数y=f(x)的图象与x轴交于A点,它的反函数的图象与y轴交于B点,并且这两个函数图象交于P点,已知四边形OAPB的面积为3,则k的值为 ( )
A.3
B.![]() C.
C.![]() D.
D.![]()
9.设![]() 、
、![]() 为曲线
为曲线![]() :
: ![]() 的焦点,
的焦点,![]() 是曲线
是曲线![]() :
:![]() 与
与![]() 的一个交点,则
的一个交点,则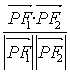 的值为
( )
的值为
( )
A.![]() B.
B.![]() C.
C.![]() D.
D. ![]()
10.已知函数![]() 在定义域
在定义域![]() 内是增函数,且
内是增函数,且![]() ,则
,则![]() 的单调情况一定是
( )
的单调情况一定是
( )
A.在![]() 上递增 B.在
上递增 B.在![]() 上递减 C.在
上递减 C.在![]() 上递减
D.在
上递减
D.在![]() 上递增
上递增
第Ⅱ卷 (非选择题 共100分)
二、填空题(本大题共6小题,每小题5分,共30分.)
11.若![]() ≥0,则
≥0,则![]() 的最小值是 .
的最小值是 .
12.曲线![]() 处的切线与x轴、直线
处的切线与x轴、直线![]() 所围成的三角形的面积为
所围成的三角形的面积为![]() =
.
=
.
13.设地球O的半径为R,P和Q是地球上两点,P在北纬![]() ,东经
,东经![]() ,Q在北纬
,Q在北纬![]() ,东经
,东经![]() ,则P与Q两地的球面距离为_____________
,则P与Q两地的球面距离为_____________
14.在![]() 的二项展开式中各项系数之和为
的二项展开式中各项系数之和为![]() ,其二项式系数之和为
,其二项式系数之和为![]() ,若
,若![]() ,则其二项展开式中
,则其二项展开式中![]() 项的系数为__________
项的系数为__________
15.已知函数f(x)对任意实数p、q满足:![]() ,
,![]() 3,则
3,则
![]() =
.
=
.
16.连接抛物线上任意四点组成的四边形可能是 (填写所有正确选项的序号).
①菱形 ②有3条边相等的四边形 ③梯形
④平行四边形 ⑤有一组对角相等的四边形
三、解答题(本大题共6小题,共74分.解答应写出文字说明、证明过程或演算步骤)
17.(本小题满分12分)
已知函数![]() 的定义域为
的定义域为![]() ,值域为
,值域为![]() .试求函数
.试求函数![]() (
(![]() )的最小正周期和最值.
)的最小正周期和最值.
18.(本小题满分14分)
袋中装有m个红球和n个白球,且 m≥n≥2,这些红球和白球除了颜色不同外,其余都相同,从袋中同时取出2个球.
(1)若取出的是2个红球的概率等于取出的是一红一白的2个球的概率的整数倍,试证m必为奇数;
(2)在m、n的数组中,若取出的球是同色的概率等于不同色的概率,试求同时满足m+n≤40的所有数组(m,n).
19.(本小题满分14分)
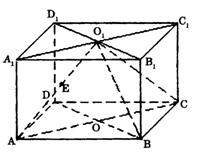
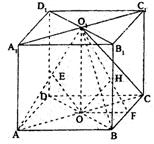
如图,直四棱柱ABCD—A1B1C1D1的高为3,底面是边长为4且∠DAB=60°的菱形,AC∩BD=0,A1C1∩B1D1=O1,E是O1A的中点.
|
(2)求点E到平面O1BC的距离.
20.(本小题满分15分)
在平面直角坐标系中,已知向量![]()
![]()
![]() 的最小值为1,
的最小值为1,![]() )
)![]() 动点P同时满足下列三个条件:
动点P同时满足下列三个条件:
(1)![]() ·
·![]()
(2)动点P的轨迹C经过点B(0,-1).
(Ⅰ)求曲线C的方程;
(Ⅱ)是否存在方向向量为m=(1,k)(k≠0)的直线l,l与曲线C相交于M、N两点,使![]() 60°?若存在,求出k值,并写出直线l的方程;若不存在,请说明理由.
60°?若存在,求出k值,并写出直线l的方程;若不存在,请说明理由.
21.(本小题满分15分)
已知数列![]() 各项均不为0,其前
各项均不为0,其前![]() 项和为
项和为![]() ,且对任意
,且对任意![]() 都有
都有![]() (
(![]() 为大于1的常数),记
为大于1的常数),记![]() .
.
(1) 求![]() ;
;
(2) 试比较![]() 与
与![]() 的大小(
的大小(![]() );
);
(3) 求证: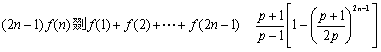 ,(
,(![]() ).
).
参考答案
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | C | A | D | C | C | B | C | B | D | A |
11. ![]() 12. ±1 13.
12. ±1 13.![]() 14.
1 15. 24 16.②③⑤
14.
1 15. 24 16.②③⑤
17.解![]()
![]()
![]()
![]()
![]()
当![]() >0时,
>0时,![]()
![]() ,
,![]()
解得![]() ,从而,
,从而,![]()
![]() ,
,
T=![]() ,最大值为5,最小值为-5;
,最大值为5,最小值为-5;
当m<0时, 解得![]() ,
,
从而,![]() ,T=
,T=![]() ,最大值为
,最大值为![]() ,
,
最小值为![]() .
.
18. (1)证明:设取出2个球是红球的概率是取出的是一红一白的2个球的概率的k倍(k为整数),则有![]() =k
=k![]() ,
,
∴![]() =kmn
=kmn![]() m=2kn+1.
m=2kn+1.
∵k∈Z,n∈Z,∴m=2kn+1为奇数.
(2)解:由题意,有![]() =
=![]() ,
,
∴![]() +
+![]() =mn.
=mn.
∴(m-n)2=m+n.∵m≥n≥2,
∴m+n≥4.∴4≤m+n≤40<72.
∴m-n的值只可能是2,3,4,5,6,相应m+n的值分别是4,9,16,25,36,
![]()
解得![]()
注意到m≥n≥2,故(m,n)数组值为(6,3),(10,6),(15,10),(21,15).
19.证明(I)过O作OF⊥BC于F,连接O1F,
∵OO1⊥面AC,∴BC⊥O1F,
∴∠O1FO是二面角O1-BC-D的平面角,…………3分
∵OB=2,∠OBF=60°,∴OF=![]() .
.
在Rt△O1OF在,tan∠O1FO=![]()
∴∠O1FO=60°即二面角O1—BC—D为60° …………6分
解(II)在△O1AC中,OE是△O1AC的中位线,∴OE∥O1C
|
过O作OH⊥O1F于H,则OH是点O到面O1BC的距
离,…………9分
点E到面O1BC的距离等于OH,![]()
∴OH=![]() ∴点E到面O1BC的距离等于
∴点E到面O1BC的距离等于![]() …………12分
…………12分
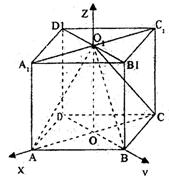
解法二:(I)∵OO1⊥平面AC,∴OO1⊥OA,OO1⊥OB,又
OA⊥OB,建立如图所示的空间直角坐标系(如图)
∵底面ABCD是边长为4,∠DAB=60°的菱形,
|
则A(2![]() ,0,0),B(0,2,0),C(-2
,0,0),B(0,2,0),C(-2![]() ,0,0),
,0,0),
O1(0,0,3)
![]()
设平面O1BC的法向量为![]() =(x,y,z),
=(x,y,z),
则![]() ⊥
⊥![]() ,
,![]() ⊥
⊥![]() ,
,
∴![]() ,则z=2,x=-
,则z=2,x=-![]() ,y=3,
,y=3,
∴![]() =(-
=(-![]() ,3,2),而平面AC的法向量
,3,2),而平面AC的法向量![]() =(0,0,3)
=(0,0,3)
∴cos<![]() ,
,![]() >=
>=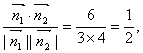 ,
,
设O1-BC-D的平面角为α, ∴cosα=![]() ∴α=60°.
∴α=60°.
故二面角O1-BC-D为60°.
(II)设点E到平面O1BC的距离为d,
∵E是O1A的中点,∴![]() =(-
=(-![]() ,0,
,0,![]() ),
),
则d=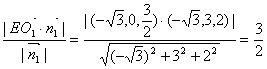
∴点E到面O1BC的距离等于![]() 。
。
20.解
|
∴![]()
由![]()
由(1)、(2)可知点P到直线x=![]() 再由椭圆的第二定义可知,点P的轨迹是椭圆,椭圆C的方程为:
再由椭圆的第二定义可知,点P的轨迹是椭圆,椭圆C的方程为:![]()
由(3)可知b=1,∴a2=b2+c2=1+2=3.
∴椭圆C的方程为![]()
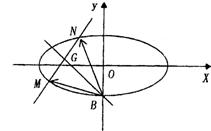
(2)设直线l的方程为:y=kx+m,设M(![]()
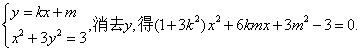
x1+x2=![]()
Δ=36k2m2-12(m2-1)(1+3k2)=12[3k2-m2+1]>0 ①
线段MN的中点G(x0,y0),
x0=![]() ,
,
线段MN的垂直平分线的方程为:y-![]()
∵![]() ∴线段MN的垂直平分线过B(0,-1)点,
∴线段MN的垂直平分线过B(0,-1)点,
∴-1-![]() ,∴m=
,∴m=![]() ②
②
②代入①,得3k2-(![]() ③
③
∵![]() °,∴△BMN为等边三角形,
°,∴△BMN为等边三角形,
∴点B到直线MN的距离d=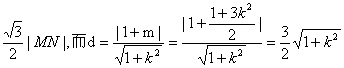
MN=![]()
![]()
=![]()
∴![]()
解得k2=![]() ③式.代入②,得m=
③式.代入②,得m=![]()
直线l的方程为:y=![]()
21.解:(1) ∵![]() , ①
, ①
∴![]() . ②
. ②
②-①,得![]() ,即
,即![]() .在①中令
.在①中令![]() ,可得
,可得![]() .
.
∴![]() 是首项为
是首项为![]() ,公比为
,公比为![]() 的等比数列,
的等比数列,![]() .
.
(2) 由(1)可得
![]() .
.
![]()
![]() .
.
∴![]()
![]() ,
,
![]()
![]() .
.
而![]()
![]() ,且
,且![]() ,
,
∴![]() ,
,![]() .∴
.∴![]()
![]()
![]() ,(
,(![]() ).
).
(3) 由(2)知 ![]() ,
,![]()
![]()
![]() ,(
,(![]() ).
).
∴当![]() 时,
时,![]() .
.
∴![]()
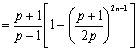 ,
,
(当且仅当![]() 时取等号).
时取等号).
另一方面,当![]() ,
,![]() 时,
时,
![]()
![]()
![]()
![]() .
.
∵![]() ,∴
,∴![]() .
.
∴![]() ,(当且仅当
,(当且仅当![]() 时取等号).
时取等号).
∴![]() .
.
(当且仅当![]() 时取等号).
时取等号).
综上所述,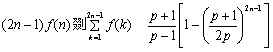 ,(
,(![]() ).
).