2006-2007学年度上学期
高中学生学科素质训练
高三数学第一轮复习单元测试(3)—《三角函数》
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知![]() 则
则![]() 等于 ( )
等于 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.将函数![]() 的图象按向量
的图象按向量![]() 平移,平移后的图象如图所示,则平
平移,平移后的图象如图所示,则平
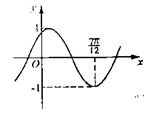 移后的图象所对应函数的解析式是 ( )
移后的图象所对应函数的解析式是 ( )
A.![]()
B.![]()
C.![]()
D.![]()
3.已知函数![]() 在区间
在区间![]() 上的最小值是
上的最小值是![]() ,则
,则![]() 的最小值等于 ( )
的最小值等于 ( )
A.![]() B.
B.![]() C.2 D.3
C.2 D.3
4.设![]() ,对于函数
,对于函数![]() ,下列结论正确的是 ( )
,下列结论正确的是 ( )
A.有最大值而无最小值 B.有最小值而无最大值
C.有最大值且有最小值 D.既无最大值又无最小值
5.已知非零向量![]() 与
与![]() 满足
满足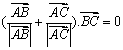 且
且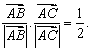 则
则![]() 为 ( )
为 ( )
A.等边三角形 B.直角三角形
C.等腰非等边三角形 D.三边均不相等的三角形
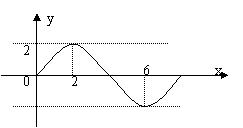
6.下列函数中,图像的一部分如右图所示的是 ( )
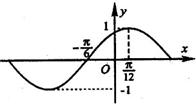 A.y=sin(x+
A.y=sin(x+![]() )
)
B.y=sin(2x-![]() )
)
C.y=cos(4x-![]() )
)
D.y=cos(2x-![]() )
)
7.若△![]() 的内角
的内角![]() 满足
满足![]() ,则
,则![]() = ( )
= ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.△ABC的三内角![]() 所对边的长分别为
所对边的长分别为![]() 设向量
设向量![]() ,
,![]() ,若
,若![]() ,则角
,则角![]() 的大小为 ( )
的大小为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.函数![]() 的最小正周期是 ( )
的最小正周期是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.设a b c分别是ΔABC的三个内角ABC所对的边,则a2=b(b+c)是A=2B的 ( )
A.充要条件 B.充分而不必要条件
C.必要而不充分条件 D.既不充分也不必要条件
11. ![]() 等式
等式![]() 成立
成立![]() 是
是![]()
![]() 成等差数列
成等差数列 ![]() 的 ( )
的 ( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分又不必要条件
12.如果![]() 的三个内角的余弦值分别等于
的三个内角的余弦值分别等于![]() 的三个内角的正弦值,则( )
的三个内角的正弦值,则( )
A.![]() 和
和![]() 都是锐角三角形
都是锐角三角形
B.![]() 和
和![]() 都是钝角三角形
都是钝角三角形
C.![]() 是钝角三角形,
是钝角三角形,![]() 是锐角三角形
是锐角三角形
D.![]() 是锐角三角形,
是锐角三角形,![]() 是钝角三角形
是钝角三角形
二、填空题:本大题共4小题,每小题4分,共16分,把答案填在题中横线上.
13.已知![]()
![]() ,sin(
,sin(![]() )=-
)=-![]()
![]() 则
则![]() =___ _.
=___ _.
14.给出下面的3个命题:(1)函数![]() 的最小正周期是
的最小正周期是![]() ;(2)函数
;(2)函数![]() 在区间
在区间![]() 上单调递增;(3)
上单调递增;(3)![]() 是函数
是函数![]() 的图象的一条对称轴.其中正确命题的序号是
.
的图象的一条对称轴.其中正确命题的序号是
.
15. ![]() 的值为
.
的值为
.
16.函数![]() 的图象如图所示,则
的图象如图所示,则![]() 的值等于
.
的值等于
.
三、解答题:本大题共6小题,共74分.解答应写出文字说明、证明过程或演算步骤.
17.(本小题满分12分)(2006年四川卷)已知![]() 是三角形
是三角形![]() 三内角,向量
三内角,向量![]() ,且
,且![]() .
.
(1)求角![]() ;
;
(2)若![]() ,求
,求![]() .
.
18.(本小题满分12分)(2006年上海春卷)已知函数
![]() .
.
(1)若![]() ,求函数
,求函数![]() 的值;
的值;
(2)求函数![]() 的值域.
的值域.
19.(本小题满分12分)(2006年安徽卷)已知![]() .
.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)求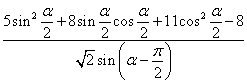 的值.
的值.
20.(本小题满分12分)有一块半径为R,中心角为45°的扇形铁皮材料,为了获取面积最大的矩形铁皮,工人师傅常让矩形的一边在扇形的半径上,然后作其最大内接矩形,试问:工人师傅是怎样选择矩形的四点的?并求出最大面积值.
21.(本小题满分12分)设![]() ,函数
,函数![]() 的定义域为
的定义域为![]() ,且
,且![]()
![]() ,对定义域内任意的
,对定义域内任意的![]() ,满足
,满足![]() ,求:
,求:
(1)![]() 及
及![]() 的值;
的值;
(2)函数![]() 的单调递增区间;
的单调递增区间;
(3)![]() 时,
时,![]() ,求
,求![]() ,并猜测
,并猜测![]()
![]() 时,
时,![]() 的表达式.
的表达式.
22.(本小题满分14分)(2006年福建卷)已知函数![]()
(1)求函数![]() 的最小正周期和单调增区间;
的最小正周期和单调增区间;
(2)函数![]() 的图象可以由函数
的图象可以由函数![]() 的图象经过怎样的变换得到?
的图象经过怎样的变换得到?
参考答案(3)
1.B.∵![]() ,
,![]() , ∴
, ∴ ![]() ,
, ![]() ,
,
∴ 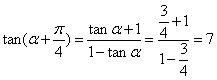 .
.
2.C. 将函数![]() 的图象按向量
的图象按向量![]() 平移,平移后的图象所对应的解析式为
平移,平移后的图象所对应的解析式为![]() ,由图象知,
,由图象知,![]() ,所以
,所以![]() ,因此选C.
,因此选C.
3.B.∵ ![]() 的最小值是
的最小值是![]() 时
时 ![]()
∴![]() ∴
∴![]() 且
且![]()
∴![]() 故本题的答案为B.
故本题的答案为B.
4.B. 令![]() ,则函数
,则函数![]() 的值域为函数
的值域为函数![]() 的值域,又
的值域,又![]() ,所以
,所以![]() 是一个减函减,故选B.
是一个减函减,故选B.
5.A 向量和三角形之间的依赖关系,认识角平分线和高及夹角用两向量数量积包装的意义, 注意 ![]() 知,角A的平分线和BC的高重合, 则
知,角A的平分线和BC的高重合, 则![]() ,由
,由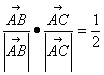 知,夹角A为600,则
知,夹角A为600,则![]() 为等边三角形,选A.
为等边三角形,选A.
6.D 由图像可知,所求函数的周期为![]() 排除(A)(C)对于(B)其图像不过(
排除(A)(C)对于(B)其图像不过(![]() ,0)点,所以应选D.
,0)点,所以应选D.
7.A.∵![]() ,∴
,∴![]() . ∴
. ∴![]() ,
,
![]() =
=![]()
![]()
![]() .应选A.
.应选A.
8.B. ![]() ,利用余弦定理可得
,利用余弦定理可得![]() ,即
,即![]() ,故选择答案B.
,故选择答案B.
9.D. ![]() 所以最小正周期为
所以最小正周期为![]() ,故选D.
,故选D.
10.A 由余弦定理得a2=b2+c2-2bccosA,所以a2=b(b+c)+c2-bc-2bccosA中c2-bc-2bccosA=c(c-b-bcosA)=2Rc(sinC-sinB-2sinBcosA)=Rc(sin(A+B)-sinB-2sinBcosA)=Rc(sin(A-B)-sinB)(*),因为A=2B,所以(*)=0,即得a2=b(b+c);而当由余弦定理和a2=b(b+c)得bc=c2-2bccosA,l两边同时除以c后再用正弦定理代换得sinB=sinC-2sinBcosA,又在三角形中C=π-(A+B),所以sinB=sin(A+B)-2sinBcosA,展开整理得sinB=sin(A-B),所以B=A-B或A=π(舍去),即得A=2B,所以应选A.
11.B 若![]()
![]() ,则“
,则“![]() ,
,![]() ,
,![]() 成等差数列”不一定成立,反之必成立,选B.
成等差数列”不一定成立,反之必成立,选B.
12.D. ![]() 的三个内角的余弦值均大于0,则
的三个内角的余弦值均大于0,则![]() 是锐角三角形,若
是锐角三角形,若![]() 是锐角三角形,由
是锐角三角形,由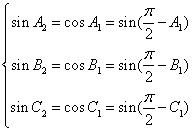 ,得
,得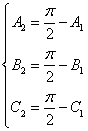 ,那么,
,那么,![]() ,所以
,所以![]() 是钝角三角形.故选D.
是钝角三角形.故选D.
13.![]() 由于
由于![]() ,所以
,所以![]() ,
,![]() ,故
,故![]() ,
,![]() ,
,![]() =
=![]() =
=![]() .
.
14.①②.③中![]() 是
是![]() 的对称中心.
的对称中心.
15.![]() .诱导公式变角,再逆用三角公式切入,
.诱导公式变角,再逆用三角公式切入,
![]() =
=![]()
16.![]() .由图象知
.由图象知![]() ,其图象关于点
,其图象关于点![]() 对称知,
对称知,![]()
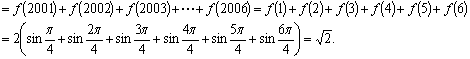
17.(1)∵![]() ∴
∴![]() 即
即![]()
![]() ,
, ![]() ,
,
∵![]() ∴
∴![]() ∴
∴![]() .
.
(2)由题知![]() ,整理得
,整理得![]() .
.
∴![]() ∴
∴![]() ,
,
∴![]() 或
或![]() .
.
而![]() 使
使![]() ,舍去
∴
,舍去
∴![]() .
.
∴![]()
![]()
![]()
![]()
![]() .
.
18.(1)![]() ,
,
![]()
![]()
![]() .
.
(2)![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
,
![]() 函数
函数![]() 的值域为
的值域为![]() .
.
19.(1)由![]() 得
得![]() ,即
,即![]() ,又
,又![]() ,所以
,所以![]() 为所求.
为所求.
(2)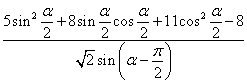 =
=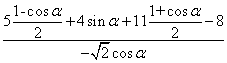
=![]() =
=![]() =
=![]() .
.
20.如下图,扇形AOB的内接矩形是MNPQ,连OP,则OP=R,设∠AOP=θ,则
∠QOP=45°-θ,NP=Rsinθ,在△PQO中,![]() ,
,
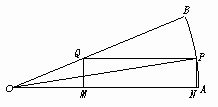
∴PQ=![]() Rsin(45°-θ).
Rsin(45°-θ).
S矩形MNPQ=QP·NP=![]() R2sinθsin(45°-θ)=
R2sinθsin(45°-θ)=![]() R2·[cos(2θ-45°)-
R2·[cos(2θ-45°)-![]() ]
]
≤![]() R2,当且仅当cos(2θ-45°)=1,即θ=22.5°时,S矩形MNPQ的值最大且最大值为
R2,当且仅当cos(2θ-45°)=1,即θ=22.5°时,S矩形MNPQ的值最大且最大值为![]() R2.
R2.
工人师傅是这样选点的,记扇形为AOB,以扇形一半径OA为一边,在扇形上作角AOP且使∠AOP=22.5°,P为边与扇形弧的交点,自P作PN⊥OA于N,PQ∥OA交OB于Q,并作OM⊥OA于M,则矩形MNPQ为面积最大的矩形,面积最大值为![]() R2.
R2.
21.(1)![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
(2)![]() ,
,
![]() 的增区间为
的增区间为![]() .
.
(3)![]()
![]() ,
,![]() ,
,
所以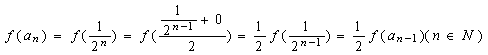 ,
,
因此![]() 是首项为
是首项为![]() ,公比为
,公比为![]() 的等比数列,故
的等比数列,故![]() ,
,
猜测![]() .
.
22.(1)![]()
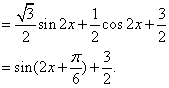
![]() 的最小正周期
的最小正周期![]()
由题意得![]()
即 ![]()
![]() 的单调增区间为
的单调增区间为![]()
(2)方法一:
先把![]() 图象上所有点向左平移
图象上所有点向左平移![]() 个单位长度,得到
个单位长度,得到![]() 的图象,再把所得图象上所有的点向上平移
的图象,再把所得图象上所有的点向上平移![]() 个单位长度,就得到
个单位长度,就得到![]() 的图象.
的图象.
方法二:
把![]() 图象上所有的点按向量
图象上所有的点按向量![]() 平移,就得到
平移,就得到![]() 的图象.
的图象.
欢迎访问 http://www.k12zy.com