衢州二中二OO六学年度第一学期高三模拟考试试卷
高三数学(文)
一、选择题(每小题5分,共50分)
1.已知集合A={1,2,3},B={2,4,6},C=![]() ,则集合C的元素之和为
,则集合C的元素之和为
(A)84 (B)50 (C)38 (D)18
2.![]() 是函数
是函数![]() 为偶函数的( )条件
为偶函数的( )条件
(A)充分 (B)必要 (C)充要 (D)既非充分又非必要
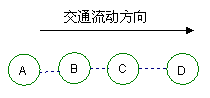 3.图示交通网络为某航空路线,A、B、C、D为该航线上的四个城市,每天只有一次航班分别到达不同城市,那么在交通流动方向上,每天从一个城市出发到达另一个城市有( )次航班
3.图示交通网络为某航空路线,A、B、C、D为该航线上的四个城市,每天只有一次航班分别到达不同城市,那么在交通流动方向上,每天从一个城市出发到达另一个城市有( )次航班
(A)4
(B)![]()
(C)![]() (D)
(D)![]()
4.正三棱锥V-ABC的底面边长为2,侧棱长![]() ,那么侧棱VC在平面VAB上的射影长( )
,那么侧棱VC在平面VAB上的射影长( )
(A)0
(B)1 (C)![]() (D)
(D)![]()
5.若![]() ,且
,且![]() ,那么
,那么![]() 的取值范围
的取值范围
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
6.O为![]() ABC内一点,且
ABC内一点,且![]() ,则
,则![]()
(A)1:2 (B)2:1 (C)1:1 (D)3:1
7.已知![]() ,过点P引与直线l成60°角的直线交平面
,过点P引与直线l成60°角的直线交平面![]() 于Q,则Q点的轨迹是
于Q,则Q点的轨迹是
(A)两个点 (B)抛物线 (C)椭圆 (D)双曲线
8.已知双曲线![]() ,F为右焦点,右准线与一条渐近线的交点P,且OP、PF、OF成等差数列,则双曲线的离心率
,F为右焦点,右准线与一条渐近线的交点P,且OP、PF、OF成等差数列,则双曲线的离心率
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
9.矩形的边长为2和5,经过它的短边上的点作直线,使得所截得的直角三角形的周长为8,则矩形留下部分面积的最小值
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
10.已知二次函数![]() 对任意
对任意![]() 恒成立,则
恒成立,则![]() 的取值范围
的取值范围
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
二、填空题(每小题4分,共16分)
11.二项式![]() 展开式中,
展开式中,![]() 的系数________________
的系数________________
12.已知实数![]() 满足
满足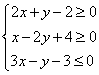 ,则
,则![]() 取值范围______________
取值范围______________
13.过抛物线![]() 的焦点F作弦AB,若
的焦点F作弦AB,若![]() ,则AB=_________
,则AB=_________
14.已知函数![]() 的反函数
的反函数![]() 的反函数
的反函数![]() ,且
,且![]() _____________
_____________
高三数学(文)模拟考试答题卷
 二、填空题(每题4分,共12分)
二、填空题(每题4分,共12分)
11 12 13 14
 三、解答题(每题14分,共84分)
三、解答题(每题14分,共84分)
15.已知向量![]() .
.
(1)当![]() 时,求
时,求![]() 的取值范围.
的取值范围.
(2)定义函数![]() ,求函数的递增区间.
,求函数的递增区间.
16.正三角形ABC的中心为O,D、E、F分别为各边的中点,三角形ABC的面积为4.
(1)以上述七个点为顶点的三角形全体记为集合M,那么集合M中共有几个元素?其中面积为1的三角形有几个?
(2)从集合M中,任取两个元素,面积均为1的概率是多少?
(3)从M中有放回地取三角形,若取出面积为1时停止,求恰好取3次后停止摸取的概率.
17.如图,三棱锥P-ABC中,![]() 为正三角形,D为AC的中点,E为PD的中点,
为正三角形,D为AC的中点,E为PD的中点,![]() .
.
 (1)求证:平面
(1)求证:平面![]() .
.
(2)求三棱锥P-ABC的体积.
18.已知数列![]() ,数列
,数列![]() 满足关系
满足关系![]() .
.
(1)求证![]() 是等差数列.
是等差数列.
(2)从第几项开始,有:![]() .
.
19.已知M(1, 3)关于直线![]() 的对称点N在椭圆
的对称点N在椭圆![]() 上,离心率
上,离心率![]() .
.
(1)求椭圆方程.
(2)过N点引两条互相垂直的直线交椭圆于A、B两点,求证直线AB恒过定点,并求出定点坐标.
20.已知函数![]() 的图象为C,且
的图象为C,且![]() .
.
(1)求a的值.
(2)已知P![]() 是曲线C上一点,设过P处曲线C的切线与x轴交于Q(t, 0),求t的最小值.
是曲线C上一点,设过P处曲线C的切线与x轴交于Q(t, 0),求t的最小值.
高三文科模拟考试参考答案
一、选择题 BCBAD CDCDD
二、![]()
![]()
![]()
![]()
三、15. (1)![]() =
=![]()
![]()
(2)![]()
16. (1)![]() ,面积为1的三角形的个数有10个;
,面积为1的三角形的个数有10个;
(2) ![]() (3)
(3)![]()
17. (2)由题意![]() ,两边平方得
,两边平方得![]()
![]()
18. (1)![]() 代入得
代入得![]() ,整理得:
,整理得:
![]() ,
,![]() ,
,![]() 为等差数列
为等差数列
(2)![]() ,所以
,所以![]() ,由
,由![]() ,得
,得![]() ,即从33项起有
,即从33项起有![]()
19. (1)![]()
(2)设AN ![]() BN
BN ![]() ,
,
由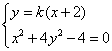 得
得![]() ,所以
,所以![]()
所以![]() ,AB的方程为
,AB的方程为![]()
令![]() ,可得
,可得![]() ,即过定点(
,即过定点(![]() )
)
20.
(1)![]()
(2)过P点的切线方程![]() ,Q在切线上,所以
,Q在切线上,所以![]() 主,
主,![]()
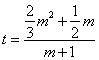 ,令
,令![]() ,得
,得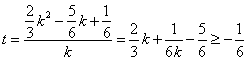
当![]() 时等号成立.
时等号成立.