第二学期学科学习能力诊断高三数学理

上海市徐汇区2006-2007学年第二学期学科学习能力诊断

高三数学（理科）2007.4

1、设集合A＝｛xx－1＜0，x∈R｝，B＝｛xx²＋x－6＜0，x∈R｝，则A∩B＝　　　

， ，， …

2、复数y＝＝　　　

3、函数y＝2cos²x＋1，（x∈R）的最小正周期为　　　

4、已知单位向量(a，(b，它们的夹角为，则3(a－(b的值为　　　

5、过点A(－1，3)且垂直于直线x－2y＋3＝0的直线方程为　　　　　 

6、在（2x－1)ⁿ的展开式中，各项系数和是　　　

7、函数f (x)＝log₂（x²－6x＋10），（x≥3）的反函数是　　　　　 

8、右表给出一个“三角形数阵”，已知第一列的数成等差数列，从第三行起，每一行的数成等比数列，且每一行的公比都相等，记第i行第j列的数为a_{i j}（i≥j，且都为自然数），则a₈₄＝________

9、如果x²＋y²≤r²（r＞0）至少覆盖f (x)＝sin的图象的一个

最大值点和一个最小值点，则r的取值范围是________

10、甲、乙两队比赛，每局甲胜的概率是，乙胜的概率也是，

则在一次五局三胜制的比赛中，甲队以3:1获胜的概率是______

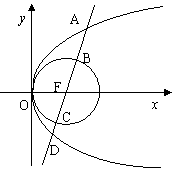
11、如图，过抛物线y²＝4x的焦点的直线依次交抛物线与圆

（x－1)²＋y²＝1于点A、B、C、D，则·＝______

12、已知奇函数f (x)满足：⑴定义域为R；⑵f (x)＜a（常数a＞0）；⑶在（0, ＋∞)上单调递增；⑷对任意一个小于a的正数d，存在一个自变量x₀，使f (x₀) ＞d，请写出一个这样的函数解析式____________

13、在⊿ABC中，若cosAcosB－sinAsinB＞0，则这个⊿一定是（　 ）

A、锐角⊿　　　B、钝角⊿　　　C、直角⊿　　　　 D、以上都有可能

14、正三棱锥底面边长为a，侧棱与底面所成角为60°，过底面一边作一截面使其与底面成30°的二面角，则此截面面积为（　 ）

A、a²　　　　B、a²　　　　 C、a²　　　　　　 D、以上都不对

15、系数为非零实数的关于x的不等式a₁ x ²+b₁ x +c₁＜0和a₂ x ²+b₂ x +c₂＜0的解集分别是M、N，

则“＝＝”是“M＝N”成立的(　　 )

A、充分不必要条件　　B、必要不充分条件　 C、充要条件　　D、既不充分也非必要条件

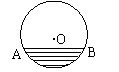16、如图所示，单位圆中弧AB的长为x，f (x)表示弧AB与弦AB所围成的弓形面积

的两倍，则函数y＝f (x)的图象是（　 ）

　 　  　

　　　(A)　　　　　　　　　(B)　　　　　　　　 (C)　　　　　　 　　(D)

17.（7+5)已知数列｛a_n｝前n项的算术平均数的倒数为 ,

⑴求｛a_n｝的通项公式；

⑵求极限：

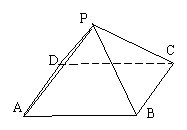18. （12’)如图所示，已知正四棱锥P-ABCD侧棱长为，底面边长为2，

E是PA的中点，试求异面直线BE与PC所成角的大小。

19. （6+8)已知关于t的方程t²－2t＋a＝0的一个根为1＋i，（a∈R）

⑴求方程的另一个根及实数a的值；

⑵若log _a（x ²＋a）≥m²－3 m＋3对x∈R恒成立，试求实数m的取值范围。

20. (14’) 如图，一客轮从O地出发，沿北偏东30°的OA方向航行，一小时后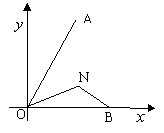

发现一乘客发病并立即发出求救信号，在距离O地40km，北偏东60°的小岛

N上有一医生，现出动离O地正东方向80km的B处的一艘快艇赶往N处载上

医生全速追赶客轮。已知快艇平均速度为40km/h，客轮平均速度为km/h，

问：最少经过多少时间，快艇可追上客轮？

21. (6＋4＋6）已知点A（－1，0)，B（1,0)，C（－ ,0)，D（,0)，动点P（x, y)满足·＝0，动点Q（x, y)满足+＝

⑴求动点P的轨迹方程C₀和动点Q的轨迹方程C₁；

⑵是否存在与曲线C₀外切且与曲线C₁内接的平行四边形，若存在，请求出一个这样的平行四边形，若不存在，请说明理由；

⑶固定曲线C₀，在⑵的基础上提出一个一般性问题，使⑵成为⑶的特例，探究能得出相应结论（或加强结论）需满足的条件，并说明理由。

22. (8＋4＋6）已知函数f (x)＝m x²＋(m－3）x＋1的图像与x轴的交点至少有一个在原点右侧，

⑴求实数m的取值范围；

⑵令t＝－m＋2，求[]；(其中[t]表示不超过t的最大整数，例如：[1]＝1， [2.5]＝2， [－2.5]＝－3)

⑶对⑵中的t，求函数g(t)＝的值域。

1、（－3,1)；2、－1；3、p ；4、；5、2x＋y－1=0；6、1；7、3＋（x≥0）；8、；

9、[，＋∞）；10、；11、1；12、或等（分段函数也可）；13～16、BCDD；

17、⑴4n－1，⑵e ；18、arctan； 19、⑴1－i，a＝4⑵[1,2]；20、2小时；21、⑴C₀：x²＋y²＝1， C₁：＋＝1，⑵连椭圆四端点可得□，⑶问题：已知C₀：x²＋y²＝1和C₁：＋＝1（a＞b＞0），试问，当a、 b满足什么条件时，对C₁上任意一点Q均存在以Q为顶点，与C₀外切，与C₁内接的平行四边形。解得a²＋b²＝a ²b²；22、⑴m≤1，⑵t＝1时[]＝1，t＞1时[]＝0，⑶｛｝∪[,)