盱眙中学2007届第二学期四月检测题
高三数学4.10
第I卷
一.选择题: 本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题意要求的．
1、从装有2个红球和2个白球的口袋内任取2个球,那么互斥而不对立的两个事件是（ ）
A.恰有1个白球;恰有2个白球 B.至少有1个白球; 至少有1个红球
C.至少有1个白球;都是白球 D.至少有1个白球;都是红球
2、若函数y=f(x+1)的定义域是［－2,3］,则y=f(2x－1)的定义域为（ ）
A.［0,
］ B.［－1,4］ C.［－5,5］ D.［－3,7］
3.若三点
、
、
不共线,则“存在唯一一对实数
、
,使
”是“
点在直线
上”的（ ）
.充分不必要条件
.必要不充分条件
.充要条件
.既不充分也不必要条件
4．已知函数
，则函数
的图像可能是( )
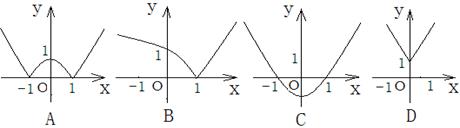
5.给出下列四个命题：
①有两个面平行，其余各面都是平行四边形的几何体是棱柱；
②有两侧面与底面垂直的棱柱是直棱柱；
③过斜棱柱的侧棱作棱柱的截面，所得图形不可能是矩形；
④所有侧面都是全等的矩形的四棱柱一定是正四棱柱。
其中正确的命题的个数为（ ）个
A、 0 B 、 1 C、 2 D、 3
6．函数f (x)为奇函数且f (3x+1)的周期为3，f (－1)=－1，则f (2008)等于（ ）
A．0 B．1 C．一1 D．2
7、已知双曲线
的离心率为
，若它的一条准线与抛物线
的准线重合。设双曲线与抛物线的一个交点为,抛物线的焦点为
，则
（ ）
.
.
.
.
8、身穿红、黄两种颜色衣服的各有2人，身穿蓝颜色衣服的有1人，现将这5人排成一行，要求穿相同颜色衣服的人不能相邻，则不同的排法共有 ( ）
A、48种 B、72种 C、78种 D、84种
9、已知三个正实数
、
、
满足
，
，则
的取值范围是（ ）
.
.
.
.
10.甲、乙两工厂2007年元月份的产值相等,甲厂的产值逐月增加,且每月增加的产值相同;乙厂产值也逐月增加,且每月增长的百分率相同,若2008年元月份两厂的产值又相等,则2007年7月份产值一定是 （ ）
A.甲厂>乙厂 B.乙厂>甲厂 C.相等 D.不能确定
第Ⅱ卷
二.填空题: 本大题共6小题，每小题5分，共30分.
11、命题：“已知
，若
”的逆否命题是：
12．已知函数
，则其导函数
展开式中含
的项的系数
为 。
13. 若
，且
，则
的值是
14. 如图，半径为2的半球内有一内接正六棱锥
，
则此正六棱锥的侧面积是________．
15、在公差为
的等差数列
中，若
是的前
项和，则数列
也成等差数列，且公差为
，类比上述结论，相应地在公比为
的等比数列
中，若
是数列的前项积，则有＝
16.定义:设有限集合
,
,则
叫做集合的模,记作
.若集合
,集合的含有三个元素的全体子集分别为
,则
=__________(用数字作答).
三.解答题:本大题共5小题，共70分，解答应写出文字说明，证明过程或演算步骤.
17.(本小题满分12分)
已知向量
，
，其中
．记
．
（1）若
的最小正周期为
，求函数的单调递增区间；
（2）若函数图象的一条对称轴的方程为
，求
的值．
18.(本小题满分14分)
已知直线
与双曲线
有A、B两个不同的交点.
（1）如果以AB为直径的圆恰好过原点O，试求k的值；
（2）是否存在k，使得两个不同的交点A、B关于直线
对称？试述理由.
19.(本小题满分14分)
在正方体ABCD—A1B1C1D1中，E是棱CC1的中点.
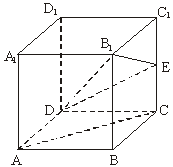
(1)判定AC与平面B1DE的位置关系，并证明;
(2)求证：平面B1DE⊥平面B1BD;
(3)求二面角B—B1E—D的大小.
20．（本小题满分14分）
已知点集
，其中
，又知点列
，
为
与
轴的的交点．等差数列
的公差为1，
．
（Ⅰ）求
；
（Ⅱ）若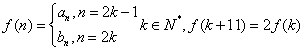
，求出
的值；
（Ⅲ）对于数列
，设
是其前项和，是否存在一个与无关的常数
，使
，若存在，求出此常数，若不存在，请说明理由．
21. (本小题满分16分)
若定义在区间D上的函数y＝f（x）对于区间D上的任意两个值x1、x2总有以下不等式≤f（）成立，则称函数y＝f（x）为区间D上的凸函数．
（1）证明：定义在R上的二次函数f（x）＝ax2＋bx＋c（a＜0）是凸函数；
（2）设f（x）＝ax2＋x（a∈R，a≠0），并且x∈［0，1］时，f（x）≤1恒成立，求实数a的取值范围，并判断函数f（x）＝ax2＋x（a∈R，a≠0）能否成为R上的凸函数；
（3）定义在整数集Z上的函数f（x）满足：
①对任意的x，y∈Z，f（x＋y）＝f（x）f（y）；
②f（0）≠0，f（1）＝2．
试求f（x）的解析式；并判断所求的函数f（x）是不是R上的凸函数说明理由．
盱眙中学2007届第二学期高三数学周练（五）
数学试题参考答案
一.选择题: 本大题共10小题，每小题5分，共50分．
1、A 2、A 3、B 4、A 5、 A
6、B 7、D 8、A 9、C 10、A
二.填空题: 本大题共6小题，每小题5分，共30分.
11、已知 ，若
；
12、
；
13、11；
14、6
；
15、
；
16、3600 .
三.解答题:本大题共5小题，共70分，解答应写出文字说明，证明过程或演算步骤.
17.(本小题满分12分)
解：
（1）
．
∵
，∴
，∴
．由
得
．
故函数的单调递增区间为
．（8分）
（2）∵直线是函数图象的一条对称轴，∴
，
，
得
．又∵，∴令
，得
．（12分）
18.(本小题满分14分)
解：（1）设
，则以AB为直径的圆恰好过原点O的充要条件是
，即
…①
由
消去y得 
…②
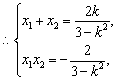
将其代入①得
，解得
或
当时，方程②为
，有两个不等实根；
当
时，方程②为
，有两个不等实根.
故当或时，以AB为直径的圆恰好过原点O. （8分）
（2）若
关于直线对称，
则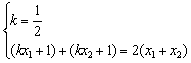
将④整理得
因为
所以
，解之，得
这个结果与③矛盾.
故不存在这样的k，使两点A、B关于直线对称. （14分）
19.(本小题满分14分)
(1)证明：延长B1E交BC的延长线于M，
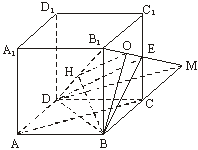
∵E为CC1的中点，
∴Rt△ECM≌Rt△EC1B1.
∴CM=B1C1=AD.又CM∥AD,
∴ACMD为平行四边形.
∴AC∥DM.
又AC
平面B1DE，DM
平面B1DE，
∴AC∥平面B1DE. （5分）
(2)证明：∵BB1⊥平面ABCD，
∴BB1⊥AC.
又ABCD为正方形，
∴BD⊥AC.
∴AC⊥平面BDB1.
∵DM∥AC,
∴DM⊥平面BDB1.
又DM平面B1DE,
∴平面B1DE⊥平面B1BD. （10分）
(3)解：作BH⊥B1D于H，由(2)知BH⊥平面B1DE，作OH⊥B1E于O，连结BO,则BO⊥B1E，
∴∠BOH为二面角B—B1E—D的平面角.
在Rt△B1BD中，BH=
=
,连结BE，则BO是等腰△BB1E的腰B1E上的高，
∴BO=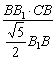
=
.
在Rt△BHO中，sin∠BOH=
=
,
∴二面角B1—BE—D的大小为arcsin. （14分）
20. (本小题满分14分)
解：（1）由题设有
，故L为直线
，它与
轴的交点为
（ 2分 ）
，又数列
是以1为公差的等差数列，所以
，
故
（ 5分 ）
（2）
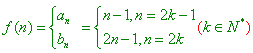（ 5分 ）
当
为奇数时，
；
当为偶数时，
． （ 10分 ）
（3）
，假设存在与
无关的常数
，使
即
，故存在与无关的常数
，使．（ 14分 ）
21. (本小题满分16分)
证明：（1）对任意x1，x2∈R，当a＜0，
有［f（x1）＋f（x2）］－2f（）＝ax12＋bx1＋c＋ax22＋bx2＋c－2［a（）2＋b（）＋c］＝ax12＋ax22－a（x12＋x22＋2x1x2）＝a（x1－x2）2 3分
∴当a＜0时，f（x1）＋f（x2）≤2f（），即≤f（）
当a＜0时，函数f（x）是凸函数． 5分
（2）当x＝0时，对于a∈R，有f（x）≤1恒成立；当x∈（0，1］时，要f（x）≤1恒成立，即ax2≤－x＋1，∴a≤－＝（－）2－恒成立，∵x∈（0，1］，∴≥1，当＝1时，（－）2－取到最小值为0，∴a≤0，又a≠0，∴a的取值范围是（－∞，0）．
由此可知，满足条件的实数a的取值恒为负数，由（1）可知函数f（x）是凸函数 11分
（3）令x＝y＝0，则f（0）＝［f（0）］2，∵f（0）≠0，∴f（0）＝1， 12分
令y＝－x，则1＝f（0）＝f（x－x）＝f（x）f（－x），故f（x）＝；
若n∈N*，则f（n）＝f［（n－1）＋1］
＝f（n－1）f（1）＝2f（n－1）＝…＝［f（1）］2； 14分
若n＜0，n∈Z，则－n∈N*，∴f（n）＝＝＝2n；∴x∈Z时，f（x）＝2x．
综上所述，对任意的x∈Z，都有f（x）＝2x； 15分
∵［20＋21］＝＞，所以f（x）不是R上的凸函数． 16分
（对任意x1，x2∈R，有［f（x1）＋f（x2）］＝［2x1＋2x2］≥×2＝f（），
所以f（x）不是R上的凸函数． 16分）