宁夏石嘴山市回民高级中学
2006～2007学年第二学期高三第二次模拟考试
理科数学参考答案及评分标准
一．选择题：
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | D | B | B | D | C | D | A | B | A | A | C | B |
二．填空题：
13． 
14．1.4 15． 2 16．①②④
三．解答题：
17、解:(1)
…2分
.…………………………………………5分
由
得 
…………………………………………7分
所以
（ 
）时， 
为增函数………………8分
(Ⅱ)由(Ⅰ)知
，即
,.……………………………10分
∴
。………………………………………12分
18、解：（Ⅰ）记“恰好选到1个曾经参加过数学研究性学习活动的同学”为事件的
，
则其概率为
…………………………………4分
（Ⅱ）随机变量X=2，3，4。
……………………6分
…………………………8分
………………………………10分
∴随机变量X的分布列为
| X | 2 | 3 | 4 |
| P |
|
|
|
∴
…………………………12分
19、解：如图，以为坐标原点建立空间直角坐标系
，
设
，则
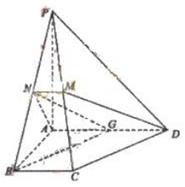
.…………………………3分
（I） 因为
，
所以
…………………………6分
（II） 因为
，
所以
，又因为
，
所以
平面
…………………………8分
设
与平面
所成的角为θ，
则sinθ=
，…………11分
所以与平面所成的角正弦值为
。…………………………12分
20、解：（Ⅰ）由框图，知数列
∴
…………3分
（Ⅱ）y1=2，y2=8，y3=26，y4=80。
由此，猜想
…………5分
证明：由框图，知数列{yn}中，yn+1=3yn+2
∴
∴
∴数列{yn+1}是以3为首项，3为公比的等比数列。
∴
+1=3·3n－1=3n ∴=3n－1（
） ……………8分
（Ⅲ）（理）zn=
=1×（3－1）+3×（32－1）+…+（2n－1）（3n－1）
=1×3+3×32+…+（2n－1）·3n－[1+3+…+（2n－1）]
记Sn=1×3+3×32+…+（2n－1）·3n，①
则3Sn=1×32+3×33+…+（2n－1）×3n+1 ② ……………10分
①－②，得－2Sn=3+2·32+2·33+…+2·3n－（2n－1）·3n+1
=2（3+32+…+3n）－3－（2n－1）·3n+1=2×
=
……………12分
∴
又1+3+…+（2n－1）=n2
∴
…………14分
21、解：（1）设M(x，y)是所求曲线上的任意一点，
P（x1，y1）是方程x2 +y2 =4的圆上的任意一点，
则
则有：
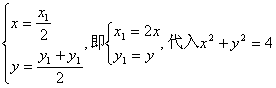得，
轨迹C的方程为
…………………………………………4分
（2）当直线l的斜率不存在时，与椭圆无交点.
所以设直线l的方程为y = k(x+2)，与椭圆交于A(x1，y1)、B(x2，y2)两点，
N点所在直线方程为
由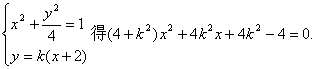
由△= 
即
…………………………………………………6分
即
，∴四边形OANB为平行四边形 …………7分
假设存在矩形OANB，则
，即
，
即
，
于是有
得
…………………………………………10分
设
， …………12分
即点N在直线
上. ∴存在直线l使四边形OANB为矩形，
直线l的方程为
………………………………………………………14分
四、选做题：
22、A、选修4—1：几何证明选讲
证明： ①连结OD． ∵DE切⊙O于点D，∴DE⊥OD, ∴∠ODE=900
又∵AD=DC, AO=OB，∴OD//BC
∴∠DEC=∠ODE=900, ∴DE⊥BC …………………………………5分
②连结BD． ∵AB是⊙O的直径, ∴∠ADB=900
∴BD⊥AC, ∴∠BDC=900
又∵DE⊥BC, Rt△CDB∽Rt△CED
∴
, ∴BC=
又∵OD=
BC，∴OD=
, 即⊙O的半径为
．…………………………10分
B、选修4—4：坐标系与参数方程
B、1、解：
的距离为：
∴
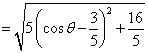
．…………………………………5分
2、解：
可表示为
，
化为直角坐标方程为
，
即
，
因此该圆的半径为5，圆心的直角坐标为
，
所以圆的半径为5，圆心的极坐标为（5，
）。…………………………………10分
C、选修4—5：不等式选讲
C、证法1：由已知条件和均值不等式有：
，
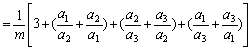
当且仅当
时，等号成立．…………………………………10分
证法2：由已知条件和柯西不等式有：
，
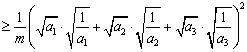
当且仅当时，等号成立．…………………………………10分