冷水江市一中2007届高三第十次高考模拟试题
数 学（文科）
命题：高三数学组
本试卷共150分。考试用时120分钟。
一、选择题（共10小题，每题5分，共50分）
1．已知
，集合
表示把集合M中的元素x映射到集合N中仍为x，则a+b的值为
（ ）
A．－1
B．0
C．1
D．
2． 对总数为N的一批零件抽取一个容量为30的样本，若每个零件被抽取的概率为
， 则N的值为
（ ）
A．120 B．200 C．150 D．100
3．已知
为偶函数，且
，当
时，
，若
，
，则
（ ）
A．2007
B．
C．2
D．－２
4．若a=（2，1），b=（1，k）, a∥b,则实数k的值为 （ ）
A．k=2
B．
C．
D． 
5．有一个等差数列
与一个等比数列
，它们的首项是一个相等的正数，且第
项也相等，则第
项的大小关系为
（ ）
A．
B．
C．
D．
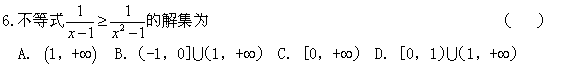
7．一个棱长为
的正三棱柱的六个顶点全部在同一个球面上,则此球的表面积为 ( )
8．已知
为第二象限角，且
那么
的取值范围是 （ ）
A．（－1，0） B．（1，
）
C．（－1，1）
D．（
）
9．从4名教师与5名学生中任选3人，其中至少要有教师与学生各一人，则不同的选法共有 种。 ( )
A．140 B．70 C．80 D．35
10．直线
与曲线
（ ）
A．没有交点 B．只有一个交点 C．有两个交点 D．有三个交点
二、填空题：（共5小题，每题5分，共25分）
11．已知曲线
在
处的切线恰好与抛物线
相切，则
=
12．把点A（2，2）按向量a=（－2，2）平移至点B，此时点B分向量
（O为坐标原点）的比为－2，则点C的坐标为
13．点（3，1）和（－4，6）在直线3x－2y＋a=0的
两侧，则实数a的取值范围是
14．
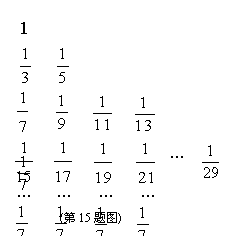
15．把数列
的所有数按照从大到小，
左大右小的原则写成如下数表：第k行有
个数，
第t行的第s个数（从左数起）记为A（t,s），
则A（8,17）=
三、解答题（共6小题，共75分）
16．(12分)已知点
（Ⅰ）若
，求
的值；
（Ⅱ）若
，其中O为坐标原点，且 
，求
的夹角的大小．
17．（12分）平面上有两个质点A（0,0），B（2,2），在某一时刻开始每隔1秒向上下左右任一方向移动一个单位，已知质点A向左右移动的概率都是，向上、下移动的概率分别是
和p ，质点B向四个方向移动的概率均为q．
(1) 求p、q的值；
(2) 试判断至少需要几秒，A、B能同时到达D（1，2）？并求出在最短时间同时到达D的概率．
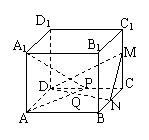
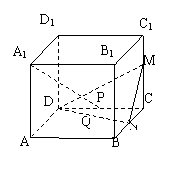18．（12分）如图，正方体ABCD—A1B1C1D1的棱长为2，M、N、P分别是棱CC1、CB、CD的中点.
⑴ 求证：
；
⑵
求四面体
的体积．
19．（12分）已知双曲线C的方程为
，离心率
.
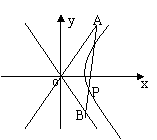（Ⅰ）求双曲线C的渐近线方程；
（Ⅱ）如图，若A、B分别是两渐近线上的点，AB是
位于第一、四象限间的线段，
的面积为定值
，
已知
，双曲线C过点P,试求双曲线C的方程．
20．（13分）已知定义在R上的函数
（a，b，c，
）的图象关于原点对称，且当
时，
取得极小值
.
（Ⅰ）求的单调递增区间；
（Ⅱ）解关于x的不等式
．
21．（14分）已知定义在R上的函数满足对任意实数
，
，总有
恒成立，已知
，若对任意的正整数n，有
，
.
（1）求数列
和
的通项公式；
（2）记
，
，试比较
与
的大小关系，并给出证明．
冷水江市一中2007届高三第十次高考模拟试题
数学（文科）参考答案
1．C；提示：由题知：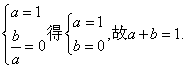
2．A；提示：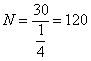
。
3．B；提示：
为偶函数，则
，故得周期为4，
4．B；
5．C；提示：
，
又
（当
时取“=”）即有
6．B
7．
8．D；提示：由题知
。
，
9．B；提示：
10．D；提示：当
时，曲线方程为
，
时，方程为
。又直线恒过点（0，3），又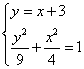
得
，解得
或
，故与左半椭圆还有一个交点；另的斜率比双曲线的渐近线
的斜率小，故与双曲线右半部份有一交点，共有3个交点。
11．16；提示
，
，故切线方程为
即
代入
中，得：
，由
12．（0，2）；提示：B（0，4），则由B分的比为-2，知C（0，2）
13．-7<a<24;提示：（9-2+a）(-12-12+a)<0
14．-20
15．
；提示：前7行共有
个数，故第8行的第一个数为
，那么第8行的第17个数为
16．解：（Ⅰ）
，由
得
得
，平方得
。
（Ⅱ）
又 
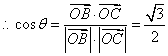
17．解：⑴
;
⑵至少需要3秒才可同时到达D；
恰好经过3秒，A到达D点的概率为
,
设
，则经过3秒，B到达D的可能情形为DBD、DMD、DED、DCD、NBD、NCD、HBD、FED、FBD共有九种情形，故B到达D点的概率为
，
在最短时间同时到达D的概率为
.
18．⑴证明：正方体ABCD—A1B1C1D1中，
在底面ABCD内的射影为AP，在正方形ABCD中，P、N为CD、BC中点，记AP与DN交于
一点Q，则
，
同理可证
。
⑵取BB1中点E，连NE，则
，且
为梯形，且
19．.解(Ⅰ) 渐近线方程为
；
(Ⅱ) 不妨设
，其中
，
，设渐近线
的倾斜角为
，则
，所以
，从而由
得
，又设
，则点
，将其代入双曲线
中得
，则
.
双曲线C的方程为
.
20． 解(Ⅰ)由已知得为奇函数且
，
，
， 当
时，取得极小值
得
令
得：
或
的增区间为
和
.
(Ⅱ)由（1）知
故
可化为
当
时，
当
时，
m或
.
当
时，或
.
21．
解（1）：由可知
即
又可得
.
即：
，即
.
而
.
（2）由（1）可知
又
.