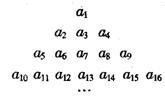祁阳二中高三第二次月考数学（理科）试题
本试卷分为第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，满分150分。考试用时120分钟。考试结束后，只需将答题卷交回。
第Ⅰ卷（共50分）
一、选择题（本题每小题5分，共50分）
1．函数
的定义域是 （ ）
A．（1，+
） B．
C．
D．（－，－1）
2．用列举法表示集合
n
N*}，正确的是 （ ）
A．
B．
C．
D．
3.
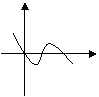
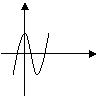
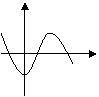
至少有一个负的实根的充要条件是
（
）
A
B
C
D
或
 |
|
 | |||||||||||||
 |  |  | |||||||||||
|
|
| |||||||||||
5、下列大小关系正确的是 ( )
（A）
(B)
(C) 
(D)
6、在等比数列{an}中，已知Sn=3n +b,则b的值为 （ ）
A、1 B、-1 C. 0 D. 任意实数
7．等差数列
（ ）
A．3 B．6 C．10 D．9
8．曲线f(x)=x3+x－2在P0点处的切线平行于直线y=4x－1，则P0点的坐标为 （ ）
A．（1，0） B．（2，8）
C．（1，0）和（－1，－4） D．（2，8）和（－1，－4）
9．设函数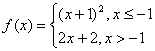
，已知
，则a的取值范围是 （ ）
A．
B．
C．
D．（－2，－
）∪（1，+∞）
10．设函数
是定义在R上的以3为周期的奇函数，若
，则实数a的取值范围是 （
）
A．
B．
C．
D．
第Ⅱ卷（共100分）
二、填空题：本大题共5小题，每小题5分，共25分。
11若
=2,则a=__________
12．若数列{
}满足：
，
，
则
的值为
.
13．若对于任意
, 函数
的值恒大于零, 则
的取值范围是 .
14、某电脑公司计划在2006年5月1日将500台电脑投放市场，经市场调研发现，该批电脑每隔10天平均日销售量减少2台，现准备用38天销售完该批电脑，则预计该公司5月1日至5月10日的平均日销售量是________台
|
的各项排成如右侧三角形状：
记
则结论
①A（2，3）=16；
②A（i，3）=2A（i，2）（i≥2）；
③[A（i，i）]2=A（i，1）·A（i，2i－1），（i≥1）；
④A（i+1，1）=A（i，1）·22i－1，（i≥1）；
中正确的是 （与出所有正确结论的序号）.
三、解答题（本大题共6小题，解答应写出文字说明，证明过程或演算步骤）
16．（本小题满分12分）已知集合A={xx2－4x+3≥0}，B={x 
<0}，U=R
求：（1）A∩B （2）（CUA）∩B
17．（本小题满分12分）
若函数
相切，并且切点的横坐标依次成的等差数列，且公差为
（I）求m的值；
（II）若点A（
是
图象的对称中心，且
，求点A的坐标.
18．（本小题满分12分）
已知
的两个根，不等式
对任意实数
恒成立；Q：函数
上有极值. 求使“P且Q”为真命题的m的取值范围.
19．（本小题满分12分）
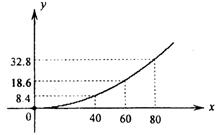
行驶中的汽车在刹车时由于惯性作用，要继续往前滑行一段距离才能停下，这段距离叫做刹车距离.在某种路面上，某种型号汽车的刹车距离y(米)与汽车的车速x(千米/时)满足下列关系：
(m,n是常数)，如图是根据多次实验数据绘制的刹车距离y(米)与汽车的车速x(千米/时)的关系图.
|
（II）如果要求刹车距离不超过25.2米，求行
驶的最大速度.
20．（本小题满分13分）
设函数
（I）k为何值时，f(x)在R上是减函数；
（II）试确定实数k的值，使的极小值为0.
21．（本小题满分14分）
函数
的反函数为
，数列{an}满足：a1=1，an+1=
，数列{bn} 满足
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）求数列{bn}的通项公式和它的前n项和Tn.
祁阳二中高三第二次月考数学试题
参考答案
一、选择题（本题每小题5分，共50分）
BCCCC BBCAD
二、填空题:（本题每小题5分，共25分）
11. 4； 12. 102； 13. x＞3或x＜1 ； 14. 16； 15．①②③④
三、解答题：
16解：由A={xx2－4x+3≥0}={x x≤1，或x≥3} …………………2分
B={x
}={x 
<x<
}………………6分
（1）A∩B={x x≤1，或x≥3}∩{x<x< }
={x <x≤1，或3≤x<} …………………………8分
（2）CUA∩B={x 1<x<3}∩{x <x<}
={x 1<x<3}……………………………………12分
17．解：（I）
……………………………………………………（4分）
的图象与y=m相切.
的最大值或最小值.即
………………（6分）
（II）又因为切点的横坐标依次成的等差数列，且公差为
所以最小正周期为
又
………………………………………（8分）
即
………………………………………………（9分）
令
则
……………………（10分）
由
得k=1,2，
因此对称中心为
、
…………………………………………（12分）
18．解：由题设
，
当时，
的最小值为3.
要使m－5<x1－x2对任意实数恒成立，
只须m－5≤3，
即
.……………………………………………………………………（3分）
由已知，得
，
此一元二次方程的判断式
………（5分）
若
有两个相等的实根
，且
的符号如下：
| x |
|
| （ |
|
| + | 0 | + |
因此，f（）不是函数的极值.…………………………………………（7分）
若
，则
有两个不等的实根
和
，且的符号如下：
| x | （－∞， |
| （ |
| （ |
|
| + | 0 | － | 0 | + |
） 因此，函数在
处取得极大值，在
处取得极小值.………………（9分）
综上所述，当且仅当时，函数在（－∞，+∞）上有极值.
由
即当
正确.……………………………………………………（11分）
综上，当
时，命题“P且Q”为真命题.………………………………（12分）
19．本题主要考查函数的基本性质、解析式、图象不等式等知识以及运用这些知识解决实际应用问题的能力。满分12分
解：（Ⅰ）依题意得：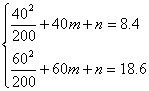
………………4分
解得：
…………6分
（Ⅱ）∵
………………8分
得－72≤x≤70 ∵x≥0 ∴0≤x≤70
答：行驶的最大速度是70千米/时 ………………12分
20．本题主要考查导数、函数单调性、极值等知识考查分类讨论思想和综合应用能力，满分13分。
解：（Ⅰ）∵
∴
………………2分
当k=4时，
………………4分
∴当k=4时，
上是减函数
（Ⅱ）当k≠4时，令
当k<4时，即
有
| x |
|
| （ | 2 | （2，+∞） |
|
| － | 0 | + | 0 | － |
|
| ↘ | 极小 | ↗ | 极大 | ↘ |
令
∴k=0 ………………10分
②当k>4时，即
>2有
| x |
| 2 | （2， |
| （ |
|
| － | 0 | + | 0 | － |
|
| ↘ | 极小 | ↗ | 极大 | ↘ |
令
∴k=8
∴当k=0或k=8时，
有极小值0 ………………13分
20．本题主要考查等差数列、等比数列、不等式等的基本知识、基本运算和综合应用的能力。满分20分
解：（Ⅰ）∵
∴
………………2分
∴
即
∴数列
为首项，公差为1的等差数列 …………4分
∴
…………6分
（2）由于
所以
以上两式相减得当 
它对n=1也适合，所以
+n （n∈N*） ………………10分
数列{bn}的前n项和Tn=（21+1）+（22+2）+…+（2n+n）
=（21+22+…+2n）+（1+2+…+n）
=
…………14分
欢迎访问 http://www.k12zy.com