衡阳县一中2008届高三第二次月考试题
数学(理科)
考生须知:
1. 本卷满分150分, 考试时间120分钟.
2. 所有答案必须写在答题卷上, 写在试题卷上无效.
3. 考试结束, 只需上交答题卷.
一. 选择题 : (本大题共10小题, 每小题5分, 共50分. 在每小题有且只有一个选项是符合题目要求).
1. 已知集合M ={ m m = i n , n ÎN }, 则下面属于M的元素是( )
A
.( 1 – i ) + (1+ i ) B. (1 –
i ) ( 1 + i ) C. ![]() D. (
1 – i )2
D. (
1 – i )2
2.若全集![]() ,
,![]() ,
,![]() ,则
,则![]() 为
为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.条件![]() ,条件
,条件![]() ,则
,则![]() 是
是![]() 的 ( )
的 ( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分又不必要条件
4.已知函数![]() 的反函数. 若
的反函数. 若![]() 的图象过点(3,4),则a等于 ( )
的图象过点(3,4),则a等于 ( )
A.![]() B.
B.![]() C.
C.![]() D.2
D.2
5.若![]() 是奇函数,且在(0,+∞)上是增函数,且
是奇函数,且在(0,+∞)上是增函数,且![]() ,则
,则![]() 的解是
的解是
( )
A.(-3,0)∪(3,+∞) B.(-∞,-3)∪(0,3)
C.(-∞,-3)∪(3,+∞) D.(-3,0)∪(0,3)
6. 如果f '(x)是二次函数, 且 f '(x)的图象开口向上,顶点坐标为(1,-), 那么曲线y=f(x)上任一点的切线的倾斜角α的取值范围是( )
A. (0, ) B. [0, )∪[, π) C. [0, ]∪[, π] D. [,]
7.若![]() ,则常数a,b的值为( )
,则常数a,b的值为( )
A.![]() , B.
, B. ![]() , C.
, C. ![]() , D.
, D. ![]()
8.在R上定义运算![]() :
:![]() ,若不等式
,若不等式![]() 对任意实数
对任意实数![]() 都成立,则实数
都成立,则实数![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D. ![]()
9.若不等式![]() 对于任意正整数n恒成立, 则实数a的取值范围是
对于任意正整数n恒成立, 则实数a的取值范围是
A.![]() B.
B.![]()
C.![]() D.
D.![]()
10.已知函数![]() 的图象如下所示
的图象如下所示
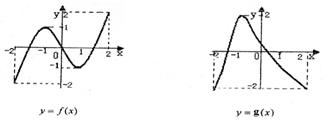
给出下列四个命题:
(1)方程![]() 有且仅有6个根 (2)方程
有且仅有6个根 (2)方程![]() 有且仅有3个根
有且仅有3个根
(3)方程![]() 有且仅有5个根 (4)方程
有且仅有5个根 (4)方程![]() 有且仅有4个根
有且仅有4个根
其中正确的命题个数是( ).
A.4个 B.3个 C.2个 D.1个
二.填空题: (本大题有5小题, 每小题5分, 共25分.)
11.已知函数![]() 的图象在点
的图象在点![]() 处的切线方程是
处的切线方程是![]() ,则
,则![]() ____.
____.
12在等差数列![]() 中,
中,![]() 为
为![]() 的前
的前![]() 项和,若
项和,若![]() ,则
,则![]() __________.
__________.
13.已知正数![]() 、
、![]() 满足
满足![]() ,则
,则![]() 的最小值为__________.
的最小值为__________.
14.设奇函数f(x)在[-1,1]上是增函数,且f(-1)=-1,若函数f(x)![]() t
t![]() -2at+1对所有的x
-2at+1对所有的x![]() [-1,1]都成立,则当a
[-1,1]都成立,则当a![]() [-1,1]时,t的取值范围是________________。
[-1,1]时,t的取值范围是________________。
15.关于函数![]() ,(
,(![]() 是常数且
是常数且![]() >0)。对于下列命题:
>0)。对于下列命题:
①函数![]() 的最小值是 -1;②函数
的最小值是 -1;②函数![]() 在每一点处都连续;③函数
在每一点处都连续;③函数![]() 在R上存在反函数;④函数
在R上存在反函数;④函数![]() 在
在![]() 处可导;⑤对任意
处可导;⑤对任意![]() 且
且![]() ,恒有
,恒有![]() 。
。
其中正确命题的序号是 .
.
三. 解答题: (本大题有6小题, 共75分. 解答应写出文字说明, 证明过程或演算步骤.)
16.(本小题满分12分)已知函数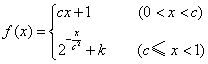 在区间
在区间![]() 内连续,且
内连续,且![]() .
.
(1)求实数![]() 和
和![]() 的值;
的值;
(2)解不等式![]() .
.
17. (本小题满分12分)已知二次函数![]() 的二次项系数为
的二次项系数为![]() ,且不等式
,且不等式![]() 的解集为
的解集为![]()
![]()
⑴若方程![]() 有两个相等的实数根,求
有两个相等的实数根,求![]() 的解析式;
的解析式;
⑵若函数![]() 无极值,求实数
无极值,求实数![]() 的取值范围
的取值范围![]()
18.(本小题满分12分)已知![]()
(1)若![]() 在
在![]() 上是增函数, 求
上是增函数, 求![]() 的取值范围;
的取值范围;
(2)若![]() 求
求![]() 的值, 并求
的值, 并求![]() 的最小值.
的最小值.
19.(本小题满分13分) 某公司生产的A型商品通过租赁柜台进入某商场销售.第一年,商场为吸引厂家,
决定免收该年管理费,因此,该年A型商品定价为每件70元,年销售量为11.8万件.第二年,商场开始对该
商品征收比率为p%的管理费(即销售100元要征收p元),于是该商品的定价上升为每件![]() 元,预计年销售量将减少p万件.
元,预计年销售量将减少p万件.
(1) 要使第二年商场在此项经营中收取的管理费不少于14万元,则商场对该商品征收管理费的比率p%的范围是多少?
(2) 第二年,商场在所收管理费不少于14万元的前提下,要让厂家获得最大销售金额,则p应为多少?
20.(本小题满分13分)已知函数![]()
(1)求证:函数![]() 上是增函数.
上是增函数.
(2)若![]() 上恒成立,求实数a的取值范围.
上恒成立,求实数a的取值范围.
(3)若函数![]() 上的值域是
上的值域是![]() ,求实数a的取值范围.
,求实数a的取值范围.
21.(本小题满分13分)已知函数![]() 和点
和点![]() ,过点
,过点![]() 作曲线
作曲线![]() 的两条切线
的两条切线![]() 、
、![]() ,切点分别为
,切点分别为![]() 、
、![]() .
.
(1)设![]() ,试求函数
,试求函数![]() 的表达式;
的表达式;
(2)是否存在![]() ,使得
,使得![]() 、
、![]() 与
与![]() 三点共线.若存在,求出
三点共线.若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(3)在(Ⅰ)的条件下,若对任意的正整数![]() ,在区间
,在区间![]() 内总存在
内总存在![]() 个实数
个实数![]() ,
,![]() ,使得不等式
,使得不等式![]() 成立,求
成立,求![]() 的最大值.
的最大值.
参考答案
一.选择题: C D A D D B C C C C
二.填空题:
11.3 12. 2 13. ![]() 14.
14. ![]() 15. ①②⑤
15. ①②⑤
三.解答题:
16.解:(1)因为![]() ,所以
,所以![]() ,
,
由![]() ,即
,即![]() ,
,![]() .
.
又因为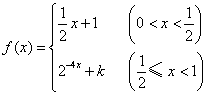 在
在![]() 处连续,
处连续,
所以![]() ,即
,即![]() .…………(6分)
.…………(6分)
(2)由(1)得: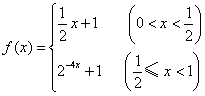
由![]() 得,当
得,当![]() 时,解得
时,解得![]() .当
.当![]() 时,解得
时,解得![]() ,
,
所以![]() 的解集为
的解集为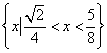 .…………(12分)
.…………(12分)
17.解:⑴设![]()
![]() ,∵不等式
,∵不等式![]() 的解集为
的解集为![]()
![]()
∴![]() ……… ①
……… ① ![]() ……… ②
……… ②
又∵![]() 有两等根,
有两等根,
∴![]() ……… ③ 由①②③解得
……… ③ 由①②③解得 ![]() …………(5分)
…………(5分)
又∵![]() ,∴
,∴![]() ,故
,故![]() .
.
∴![]() ……………………………………………(7分)
……………………………………………(7分)
⑵由①②得![]() ,∴
,∴![]() ,
,
![]() …………………………………………(9分)
…………………………………………(9分)
∵![]() 无极值,∴方程
无极值,∴方程![]()
![]() ,解得
,解得![]() ………………(12分)
………………(12分)
18. 解:(1)![]() 在
在![]() 上恒成立,
上恒成立,
![]() 又当
又当![]() 时, 仅当
时, 仅当![]() 时,
时,![]() . 又
. 又![]()
令![]()
![]() 综上,
综上,![]() …………(6分)
…………(6分)
(2)![]()
由已知![]()
解之得![]()
这时,![]() 其定义域为
其定义域为![]()
令![]() 且在
且在![]() 附近,
附近,![]() 左负右正,
左负右正,![]() 在
在![]() 处,
处,
![]() 取得极小值,
取得极小值,![]()
![]() 在定义域内连续,且
在定义域内连续,且![]() 为单峰函数,
为单峰函数,
![]()
![]() =
=![]() 极小=
极小=![]() …………(12分)
…………(12分)
19. (本小题13分)
解:(1)依题意,第二年该商品年销售量为(11.8-p)万件,
年销售收入为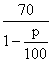 (11.8一p)万元,
(11.8一p)万元,
则商场该年对该商品征收的总管理费为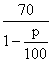 (11·8一p)p%(万元)
(11·8一p)p%(万元)
即![]() (万元)
(万元)
由![]() ≥14
≥14
化简得p2-12p+20≤0,即(p-2)(p-10)≤0,解得2≤p≤l0
故当比率为[2%,10%]内时,商场收取的管理费将不少于14万元.…7分
(2) 第二年,当商场收取的管理费不少于14万元时,
厂家的销售收入为g(p)= ![]() (2≤p≤10)
(2≤p≤10)
∵ g(p)=
![]() =700(10+
=700(10+![]() )为减函数,
)为减函数,
∴ g(p)max =g(2)=700(万元)
故当比率为2%时,厂家销售金额最大,且商场所收管理费又不少于14万元 (利用导数同样给分) ………………………13分
20..解:(1)当![]() 用定义或导数证明单调性均可.
用定义或导数证明单调性均可.
(2)![]() 上恒成立.设
上恒成立.设![]() 上恒成立.
上恒成立.
可证![]() 单调增。故
单调增。故![]() ,
,![]() 的取值范围为
的取值范围为![]()
(3)![]() 的定义域为
的定义域为![]()
当![]() 上单调增
上单调增 ![]()
故![]() 有两个不相等的正根m,n,
有两个不相等的正根m,n,![]()
当![]() 时,可证
时,可证![]() 上是减函数.
上是减函数.
![]() 综上所述,a的取值范围为
综上所述,a的取值范围为![]()
21. (本小题满分13分)
(1)设![]() 、
、![]() 两点的横坐标分别为
两点的横坐标分别为![]() 、
、![]() ,
,
![]()
![]() ,
---2分
,
---2分
∴切线![]() 的方程为:
的方程为:![]() ,
,
又![]() 切线
切线![]() 过点
过点![]() ,
, ![]() 有
有![]() ,
,
即![]() , (1)
, (1)
同理,由切线![]() 也过点
也过点![]() ,得
,得![]() .(2)
.(2)
由(1)、(2),可得![]() 是方程
是方程![]() 的两根,
的两根,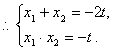 ( * )
( * )
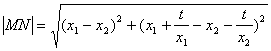
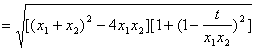 ,
,
把( * )式代入,得![]() ,
,
因此,函数![]() 的表达式为
的表达式为![]() .
---4分
.
---4分
(2)当点![]() 、
、![]() 与
与![]() 共线时,
共线时,![]() ,
,
![]()
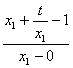 =
=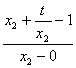 ,即
,即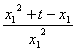 =
=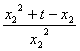 ,
,
化简,得![]() ,
,
![]() ,
,![]() . (3)
. (3)
把(*)式代入(3),解得![]() .
.
![]() 存在
存在![]() ,使得点
,使得点![]() 、
、![]() 与
与![]() 三点共线,且
三点共线,且 ![]() . ---8分
. ---8分
(3)解法![]() :易知
:易知![]() 在区间
在区间![]() 上为增函数,
上为增函数,
![]()
![]()
![]() ,
,
则![]() .
.
依题意,不等式![]() 对一切的正整数
对一切的正整数![]() 恒成立,
恒成立,
![]() ,
,
即![]() 对一切的正整数
对一切的正整数![]() 恒成立.
恒成立.
![]() ,
, ![]() ,
,
![]() . 由于
. 由于![]() 为正整数,
为正整数,![]() .
.
又当![]() 时,存在
时,存在![]() ,
,![]() ,对所有的
,对所有的![]() 满足条件.
满足条件.
因此,![]() 的最大值为
的最大值为![]() .
---13分
.
---13分
解法![]() :依题意,当区间
:依题意,当区间![]() 的长度最小时,得到的
的长度最小时,得到的![]() 最大值,即是所求值.
最大值,即是所求值.
![]() ,
,![]() 长度最小的区间为
长度最小的区间为![]() ,
,
当![]()
![]() 时,与解法
时,与解法![]() 相同分析,得
相同分析,得![]() ,
,
解得![]() .
.
后面解题步骤与解法![]() 相同(略).
相同(略).