2007年北京市海淀区数学二模文科试题.doc
一、选择题:
1.设全集U={1,3,5,7},集合A={3,5},B={1,3,7},则![]() 等于( )
等于( )
A.{5} B.{3,5} C.{1,5,7} D.{1,3,5,7}
2.已知抛物线![]() ,则它的准线方程为( )
,则它的准线方程为( )
A ![]() B
B ![]() C
C ![]() D
D ![]()
3.若![]() ,则下列结论不正确的是( )
,则下列结论不正确的是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
4.设![]() 、
、![]() 是不同的直线,
是不同的直线,![]() 、
、![]() 、
、![]() 是不同的平面,有以下四个命题:
是不同的平面,有以下四个命题:
①![]() ②
② ![]() ③
③![]() ④
④![]() ,
,
其中为真命题的是( )
A ①④ B ②③ C ①③ D ②④
5.函数![]() (
(![]() 的反函数的图象过定点
( )
的反函数的图象过定点
( )
A
![]() B
B ![]() C
C ![]() D
D ![]()
6.将圆![]() 按向量a
按向量a![]() 平移后,恰好与直线
平移后,恰好与直线![]() 相切,则实数
相切,则实数![]() 的值为( )
的值为( )
A ![]() B
B ![]() C
C ![]() D
D ![]()
7.定义在R上的函数![]() 既是偶函数又是周期函数.若
既是偶函数又是周期函数.若![]() 的最小正周期是
的最小正周期是![]() ,且当
,且当![]() 时,
时,![]() ,则
,则![]() 的值为
( )
的值为
( )
A ![]() B
B ![]() C
C ![]() D
D ![]()
8.三角形![]() 中,
中,![]() ,
,![]() ,
,![]() ,则
,则![]() 的值为( )
的值为( )
A ![]() B
B ![]() C
C ![]() D
D ![]()
二、填空题:
9.一个单位有业务人员120人,管理人员16人,后勤服务人员24人.为了了解这些职工的某种情况,要从中抽取一个容量为20的样本,用分层抽样的方法抽取样本,则其中需抽取管理人员 人
10.曲线![]() 在点(1,0)处的切线的斜率为
在点(1,0)处的切线的斜率为
11.已知点![]() 和向量a
和向量a![]() ,若
,若![]() a,则点
a,则点![]() 的坐标为
的坐标为
12.某地球仪上北纬![]() 纬线的周长为
纬线的周长为![]() cm,则该地球仪的半径是
cm,表面积为
cm2
cm,则该地球仪的半径是
cm,表面积为
cm2
13.已知函数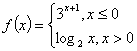 ,若
,若![]() ≥1,则
≥1,则![]() 的取值范围是
的取值范围是
14.有这样一种数学游戏:在![]() 的表格中,要求每个格子中都填上1、2、3三个数字中的某一个数字,并且每一行和每一列都不能出现重复的数字.若游戏开始时表格的第一行第一列已经填上了数字1(如左图),则此游戏有
种不同的填法;若游戏开始时表格是空白的(如右图),则此游戏共有
种不同的填法
的表格中,要求每个格子中都填上1、2、3三个数字中的某一个数字,并且每一行和每一列都不能出现重复的数字.若游戏开始时表格的第一行第一列已经填上了数字1(如左图),则此游戏有
种不同的填法;若游戏开始时表格是空白的(如右图),则此游戏共有
种不同的填法
| 1 | ||
三、解答题:
15(12分)已知![]()
![]() ,求下列各式的值:
,求下列各式的值:
(I)![]()
(II)![]()
16(13分)在某次数学实验中,要求:实验者从装有8个黑球、2个白球的袋中每次随机地摸出一个球,记下颜色后放回.现有甲、乙两名同学,规定:甲摸一次,乙摸两次.求
(I)甲摸出了白球的概率;
(II)乙恰好摸出了一次白球的概率;
(III)甲乙两人中至少有一个人摸出白球的概率.
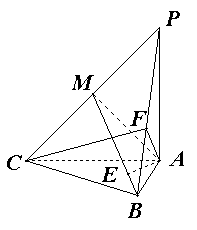
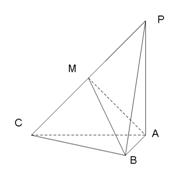 17(14分)如图,三棱锥
17(14分)如图,三棱锥![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() 为
为![]() 的中点.
的中点.
(I)求证:平面![]() 平面
平面![]() ;
;
(II)求点![]() 到平面
到平面![]() 的距离
的距离
(III)求二面角![]() 的正切值.
的正切值.
18(13分)设函数![]()
![]()
(I)当![]() 时,求函数
时,求函数![]() 的极大值和极小值;
的极大值和极小值;
(II)若函数![]() 在区间
在区间![]() 上是增函数,求实数
上是增函数,求实数![]() 的取值范围.
的取值范围.
19.(14分)已知等比数列![]() ,
,![]() 是其前
是其前![]() 项的和,且
项的和,且![]() ,
,![]() .
.
(I)求数列![]() 的通项公式;
的通项公式;
(II)设![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]()
(III)比较(II)中![]() 与
与![]() (
(![]() )的大小,并说明理由.
)的大小,并说明理由.
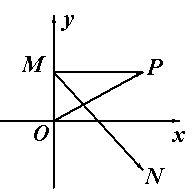 20(14分)如图,在平面直角坐标系中,已知动点
20(14分)如图,在平面直角坐标系中,已知动点![]() ,
,![]() 轴,垂足为
轴,垂足为![]() ,点
,点![]() 与点
与点![]() 关于
关于![]() 轴对称,
轴对称, ![]()
(1)求动点![]() 的轨迹
的轨迹![]() 的方程
的方程
(2)若点![]() 的坐标为
的坐标为![]() ,
,![]() 、
、![]() 为
为![]() 上的两个动点,且满足
上的两个动点,且满足![]() ,点
,点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,求
,求![]() 的最大值
的最大值
文科数学试题答案
一、选择题:
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 答案 | B | D | D | C | A | B | C | B |
二、填空题:
9. 2
10. 4
11. ![]() 12. 4
, 64
12. 4
, 64![]()
13. ![]() 14. 4
, 12
14. 4
, 12
三、解答题:
15.方法一:
(I)原式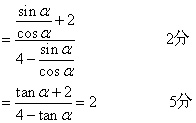
方法二:
(I)![]() ,且
,且![]() ,且由
,且由![]() ,得
,得![]() >0,
>0,![]()
所以![]() ,
,![]() 2分
2分
∴原式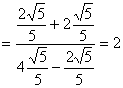 5分
5分
(II)原式![]() 7分
7分
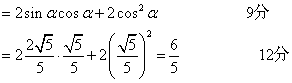
16.(I)设“甲摸出了白球”为事件![]() ,则
,则
![]() 3分
3分
(II)设“乙恰好摸出了一次白球”为事件![]() ,则
,则
![]() 8分
8分
 (III)设“甲乙两人中至少有一个人摸出白球”为事件
(III)设“甲乙两人中至少有一个人摸出白球”为事件![]() ,则
,则
![]() 13分
13分
17.方法一:(I)∵![]() ,
,![]()
∴![]() 平面
平面![]() ,故
,故![]()
∵![]() ,
,![]() 为
为![]() 的中点
的中点
∴![]() 2分
2分
∴![]() 平面
平面![]()
又![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() 4分
4分
(II)如图,在平面![]() 中作
中作![]() ,垂足是
,垂足是![]()
∵平面![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() ∴AE长为点A到平面PBC的距离
∴AE长为点A到平面PBC的距离
又∵![]() 平面
平面![]() ,∴
,∴![]()
在直角三角形![]() 中,
中,![]() ,
,![]() ,
,![]() 6分
6分
∴![]() ,∴
,∴![]() 即为所求 9分
即为所求 9分
(III)
在平面![]() 中作
中作![]() ,垂足是
,垂足是![]() ,连接
,连接![]()
∵![]() ,
,![]() ,∴
,∴![]() 平面
平面![]()
∴![]() ∴
∴![]() 是
是![]() 在平面
在平面![]() 内的射影,∴
内的射影,∴![]()
∴![]() 是二面角
是二面角![]() 的平面角,
11分
的平面角,
11分
在直角三角形![]() 中,
中,![]() ,
,![]() ,
,![]() ,可得
,可得![]()
∴在直角三角形![]() 中,
中,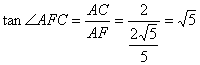 即为所求
14分
即为所求
14分
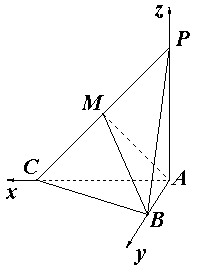 方法二:(I)同方法一
4分
方法二:(I)同方法一
4分
(II)以![]() 为原点,建立如图的空间直角坐标系
为原点,建立如图的空间直角坐标系
由已知可得各点坐标为![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() 5分
5分
设平面![]() 的法向量为n
的法向量为n![]() ,且
,且
![]() ,
,![]()
∴n![]() ,n
,n![]()
∴![]() ,
,![]() ,令
,令![]() ,可得
,可得![]() ,
,![]()
∴n![]() ,又
,又![]() ,
,
∴点![]() 到平面
到平面![]() 的距离
的距离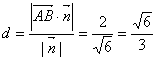 9分
9分
(III)∵![]() ,
,![]() ,∴
,∴![]() 平面
平面![]()
∴平面![]() 的法向量为
的法向量为![]() ,设二面角
,设二面角![]() 的大小为
的大小为![]()
∴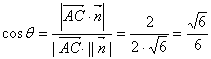 ,故
,故![]() 即为所求
14分
即为所求
14分
18.(I)当![]() 时,
时,![]() 1分
1分
∴![]() ,
2分
,
2分
令![]() ,得
,得![]() ,
,![]() ,列表
,列表
|
|
| 1 |
| 2 |
|
|
| + | 0 | ─ | 0 | + |
|
| ↗ | 极大值 | ↘ | 极小值 | ↗ |
∴![]() 的极大值为
的极大值为![]() ,
,![]() 的极小值为
的极小值为![]() 6分
6分
(II)![]() 7分
7分
①若![]() ,则
,则![]() ,此函数在
,此函数在![]() 上单调递增,满足题意 8分
上单调递增,满足题意 8分
②若![]() ,则令
,则令![]() ,得
,得![]()
![]() ,
,![]() ,由已知,
,由已知,![]() 在区间
在区间![]() 上是增函数,
上是增函数,
即当![]() 时,
时,![]() ≥0恒成立
10分
≥0恒成立
10分
若![]() ,则只须
,则只须![]() ≥1,即0
≥1,即0![]() ≤1
≤1![]() 11分
11分
若![]() ,则
,则![]() ,当
,当![]() 时,
时,![]() ,则
,则![]() 在区间
在区间![]() 上不是增函数
上不是增函数
综上所述,实数![]() 的取值范围是
的取值范围是![]() 13分
13分
19. (I)设数列![]() 的公比为
的公比为![]() ,则
,则
方法一:![]() ,
,![]() 2分
2分
∴![]() ,
,![]() ,则
,则![]() 4分
4分
方法二:易知![]() ,则
,则
![]()
![]() ,
,
则![]() 2分
2分
(以下同方法一) 4分
(II)由(I)可得,![]() ,
,
所以数列![]() 是一个以
是一个以![]() 为首项,1为公差的等差数列
5分
为首项,1为公差的等差数列
5分
∴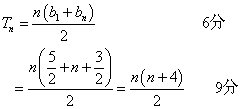
(III)∵![]() 11分
11分
∴当![]() 、2时,
、2时,![]() ,即
,即![]()
![]() 12分
12分
当![]() ≥3时,
≥3时,![]() ,即
,即![]()
![]() 14分
14分
20.(I) 由已知![]() ,
,![]() 2分
2分
则![]() ,即
,即![]() 4分
4分
(II)设![]() ,
,![]() ,如图,由
,如图,由![]() 可得
可得
![]() 5分
5分
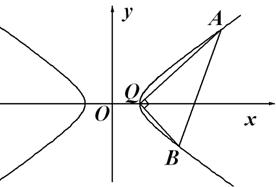 ①若直线
①若直线![]() 轴,则
轴,则![]() ,
,![]()
此时![]() ,则
,则
![]() ,解之得,
,解之得,![]() 或
或![]()
但是若![]() ,则直线
,则直线![]() 过
过![]() 点,不可能有
点,不可能有![]()
所以![]() ,此时
,此时![]() 点到直线
点到直线![]() 的距离为4
7分
的距离为4
7分
②若直线![]() 斜率存在,设直线
斜率存在,设直线![]() 的方程为
的方程为![]() ,则
,则
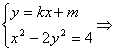
![]()
则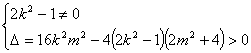 ,即
,即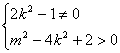
又![]() ,
,![]() 9分
9分
∴![]()
![]()
∴![]()
![]()
![]()
则![]() ,可得
,可得![]() 或
或![]()
若![]() ,则直线
,则直线![]() 的方程为
的方程为![]() ,此直线过点
,此直线过点![]() ,这与
,这与![]() 矛盾,舍
矛盾,舍
若![]() ,则直线
,则直线![]() 的方程为
的方程为![]() ,即
,即![]() 12分
12分
此时若![]() ,则直线
,则直线![]() 的方程为
的方程为![]() ,显然与
,显然与![]() 矛盾,故
矛盾,故![]()
∴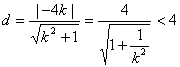 13分
13分
由①②可得,![]() 14分
14分