山东省泰安市2007年高三第二轮复习质量检测
数学(文)试题2007.5
本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分150分,考试时间120分钟.
第Ⅰ卷(选择题 共60分)
注意事项:
1.答第Ⅰ卷前,考生务必将自己的姓名、准考科目、试卷类型(A或B)用铅笔涂写在
答题卡上.
2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡
皮擦干净后,再选涂其它答案,不能答在试题卷上.
3.考试结束后,监考人员将本试卷和答题卡一并收回.
参考公式:
如果事件A、B互斥,那么 球的表面积公式
P(A+B)=P(A)+P(B) ![]()
如果事件A、B相互独立,那么 其中R表示球的半径
P(A·B)=P(A)·P(B) 球的体积公式
如果事件A在一次试验中发生的概率是
![]()
P,那么n次独立重复试验中恰好发生k 其中R表示球的半径
次的概率![]()
一、选择题:本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.
1.在复平面内,复数![]() 对应的点位于 ( )
对应的点位于 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.已知![]() ,则
,则![]() 等于 ( )
等于 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D. ![]()
3.已知等差数列![]() 的值是 ( )
的值是 ( )
A.26 B.20 C.18 D.28
4.函数![]() 给出下列三个命题;
给出下列三个命题;
①在函数![]() 上是减函数;
上是减函数;
②直线![]() 的图象的一条对称轴;
的图象的一条对称轴;
③函数![]() 的图象可以由函数
的图象可以由函数![]() 的图象向左平移
的图象向左平移![]() 得到.
得到.
其中正确的是 ( )
A.①③ B.①② C.②③ D.①②③
5.已知实数,x,y满足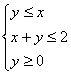 ,则
,则![]() 的最大值是 ( )
的最大值是 ( )
A.0 B.2 C.3 D.4
6.当a为任意实数时,直线![]() 恒过定点M,则以M为圆心并且与圆
恒过定点M,则以M为圆心并且与圆
![]() 相外切圆的方程是 ( )
相外切圆的方程是 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
7.一个容量为20的样本数据,分组后,组距与频数如下:![]()
![]() 2;则样本在
2;则样本在![]() 上的频率为 ( )
上的频率为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.正四棱锥P—ABCD的底面边长为2,侧棱长为![]() ,且它的五个顶点都在同一球面上,
,且它的五个顶点都在同一球面上,
则此球的体积为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
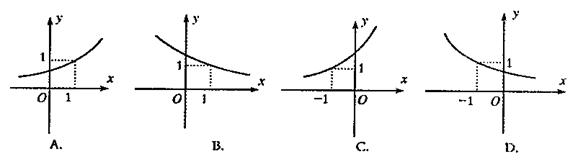
9.若函数![]() 上是减函数,则函数
上是减函数,则函数![]() 的图
的图
|
|
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11.三个数a,b,c成等比数列,若a+b+c=1,则b的取值范围为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
![]()
12.定义在R上的偶函数![]() 上是减函数;
上是减函数;![]() 是钝角三角形的两个锐角,则下列结论正确的是 ( )
是钝角三角形的两个锐角,则下列结论正确的是 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
第Ⅱ卷(非选择题 共90分)
注意事项:
1.用钢笔或圆珠笔答在试卷中(除题目有特殊规定外).
2.答卷前将密封线内的项目填写清楚.
二、填空题:本大题共4小题,每小题4分,共16分,请把答案填在题中的横线上.
13.若抛物线![]() 的焦点与双曲线
的焦点与双曲线![]() 的左焦点重合,则实数a的值是
的左焦点重合,则实数a的值是
.
|
15.已知m、n表示直线,![]() 表示
表示
平面,给出下列三个命题
①![]()
②![]()
③![]()
④![]()
其中正确命题的序号是 .
16.某市原来的民用电价为0.52元/千瓦时,换装分时电表后,峰时段(早上8点至晚上21点)的电价为0.55元/千瓦时,谷时段(晚上21点至次日早上8点)的电价为0.35元/千瓦时,对于一个平均每月用电量为200千瓦时的家庭,要使节省的电费不少于原来电费的10%,则这个家庭每月在峰时段的平均用电量至多为 .
|
17.(本小题满分12分)
在△ABC中,角A、B、C的对边分别为a、b、c,若![]()
(Ⅰ)判断△ABC的形状;
(Ⅱ)若![]() 的值.
的值.
18.(本小题满分12分)
已知各项均为正数的数列![]() ,首项为
,首项为![]() 成等差数列.
成等差数列.
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)若![]() 为数列
为数列![]() 的前n项和,则
的前n项和,则![]()
19.(本小题满分12分)
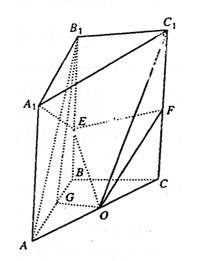
|
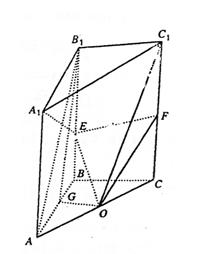
(Ⅰ)求证:OE//平面AB1C1;
(Ⅱ)求证:A1E⊥OC1.
20.(本小题满分12分)
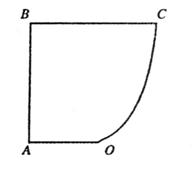
|
21.(本小题满分12分)
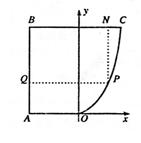
如图所示,△ABC为直角三角形,∠C=90°,若![]() 轴上,且
轴上,且![]() ,点C在x轴上移动.
,点C在x轴上移动.
(Ⅰ)求点B的轨迹E的方程;
(Ⅱ)过点![]() 的直线l与曲线E交于P、Q两点,设N(0,a)(a<0),
的直线l与曲线E交于P、Q两点,设N(0,a)(a<0),![]() 的夹角为
的夹角为![]() ,若
,若![]() 恒成立,求a的取值范围;
恒成立,求a的取值范围;
(Ⅲ)设以点N为圆心,以![]() 为半径的圆与曲线E在第一象限的交点为H,若圆在点H处的切线与曲线E在点H处的切线互相垂直,求a的值.
为半径的圆与曲线E在第一象限的交点为H,若圆在点H处的切线与曲线E在点H处的切线互相垂直,求a的值.
22.(本小题满分14分)
已知函数![]() 上单调递增,在
上单调递增,在
(-1,2)上单调递减,又函数![]() .
.
(Ⅰ)求函数![]() 的解析式;
的解析式;
(Ⅱ)求证当![]()
(Ⅲ)若函数y=m的图象与函数![]() 的图象共有3个交点,求m的取值范围.
的图象共有3个交点,求m的取值范围.
山东省泰安市2007年高三第二轮复习质量检测
数学(文)试题参考答案2007.5
一、选择题:本题共12个小题,每小题5分,共60分.
|
二、填空题:本题共4个小题,每小题4分,共16分.
13.-8 14.a 15.③ 16.118
三、解答题:本题共6个小题,共74分.
17.(本小题满分12分)
解:(I)![]() …………1分
…………1分
![]()
![]() …………3分
…………3分
即![]()
![]() …………5分
…………5分
![]()
![]() 为等腰三角形. …………7分
为等腰三角形. …………7分
(II)由(I)知![]()
![]() …………10分
…………10分
![]()
![]() …………12分
…………12分
18.(本小题满分12分)
解:(Ⅰ)由题意知![]()
当![]()
![]() ……………………2分
……………………2分
当![]()
两式相减得![]()
整理得:![]() ……………………4分
……………………4分
![]() 是以2为首项,2为公比的等比数列.
是以2为首项,2为公比的等比数列.
![]() ……………………6分
……………………6分
(Ⅱ)由(Ⅰ)知![]()
![]() …………………………7分
…………………………7分
![]() ①
①
![]() ②
②
①—②得
![]() ……………………9分
……………………9分
![]() ……………………11分
……………………11分
|
19.(本小题满分12分)
解:(I)证明:取C1C的中点F,连结EF、OF,则
OF//AC1,EF//B1C1 …………2分
∴OF∥面AB1C1,EF∥面AB1C1,…………4分
∵EF∩OF=F,AC1∩BC1=C1
∴平面OEF∥平面AB1C1…………5分
又∵OE![]() 平面OEF
平面OEF
∴OE//平面AB1C1…………6分
(II)证明:取AB的中点G,连结B1G、OG,
在直三棱柱ABC—A1B1C1中,AB=BC=AA1,
∴四边形ABB1A1为正方形
∴A1E⊥B1G …………8分
又∠ABC=90°,棱柱ABC—A1B1C1为直棱柱,
∴B1C1⊥A1E
∴A1E⊥平面GB1C1 …………10分
又OG//B1C1
∴OGB1C1共面
∴OC1![]() 平面GB1C1
平面GB1C1
∴A1E⊥OC1 …………12分
20.(本小题满分12分)
解:以O为原点OA所在直线为x轴建立直角坐标系(如图),依题意可设抛物线的方程为
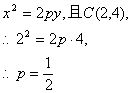
|
设![]() 是曲线段OC上的任一点,则PQ
是曲线段OC上的任一点,则PQ
=2+x,PN=4-x2 …………5分
∴工业区面积S=PQ·PN=(2+x)(4-x2)=8-x3-2 x2+4x
…………6分
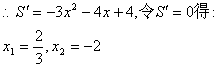
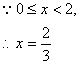 …………7分
…………7分
![]() 的增函数
的增函数
![]() 减函数;
减函数;

答:把工业园区规划成长为![]() km,宽为
km,宽为![]() km的矩形时工业园区的面积最大,最大面积是9.5km2 …………12分
km的矩形时工业园区的面积最大,最大面积是9.5km2 …………12分
21.(本小题满分12分)
解:(I)![]() 的中点
的中点
![]()
![]() …………2分
…………2分
![]()
![]() …………3分
…………3分
(II)设直线l的方程为![]()
![]()
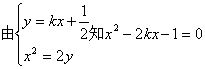
![]() …………5分
…………5分
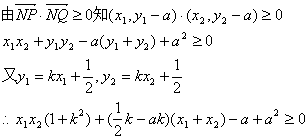
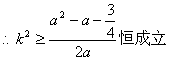 …………7分
…………7分
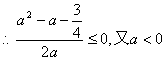
![]() …………9分
…………9分
(III)由题意知,NH是曲线C的切线,设H![]()
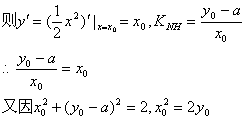
![]() …………11分
…………11分
解得a=1或a=![]()
∵a<0
![]()
![]() …………12分
…………12分
22.(本小题满分14分)
解:(I)![]()
![]() …………1分
…………1分
又函数![]() 上单调增,在(-1,2)上单调减
上单调增,在(-1,2)上单调减
![]() 的两个根 …………3分
的两个根 …………3分
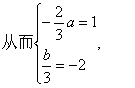
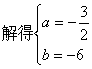
![]() …………6分
…………6分
(II)![]()
![]()
从而函数![]() 上单调增 …………7分
上单调增 …………7分
又H(4)=0
![]() …………8分
…………8分
(Ⅲ)![]() 上单调增,在(-1,2)上单调减
上单调增,在(-1,2)上单调减
且![]()
![]() 与函数
与函数![]() 的图象有3个交点.………………12分
的图象有3个交点.………………12分
又![]()
![]() 时,直线
时,直线![]() 的图象共有3个交点.……13分
的图象共有3个交点.……13分
综上:m的取值范围是![]() ………………14分
………………14分