山西省实验中学高三第五次月考
数学试题（文科）
一、选择题（本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的，把答案填在答题纸上）
1．若点P到直线
的距离与到定点（0，10）的距离之比为
，则P点的轨迹方程为
（ ）
A．
B．
C．
D．
2．直线
与连结A（2，3），B（－3，2）的线段相交，则a的范围 （ ）
A．[－1，2] B．
C．[－2，1] D．
3．两平行线
与
间距离是 （ ）
A．
B．
C．
D．
4．对于不重合的两个平面
给定下列条件 （ ）
①存在平面
使得都垂直于
②存在平面使得都平行于
③
内有不共线的三点到
距离相等
④存在异面直线l、m使得
A．1 B．2 C．3 D．4
5．若直线
绕着它与y轴的交点逆时针旋转45°,则此时直线x轴上的截距为
（ ）
A．
B．
C．
D．
6．曲线
所围成的图形面积 （ ）
A．1 B．2 C．4 D．
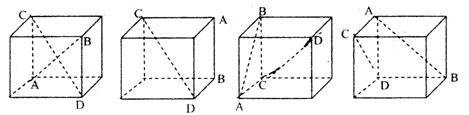
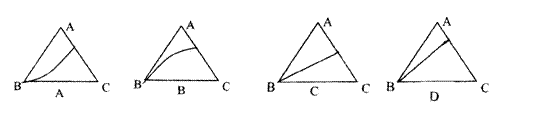7．若三菱锥A—BCD侧面ABC内一动点P到底面DBC距离与到棱AB距离相等，则动点P的轨迹与△ABC组成图形可能是 （ ）
8．A、B、C是表面积为48的球面上三点，AB=2，BC=4，∠ABC=60°，O为球心，则直线OA与截面ABC所成角的余弦值是 （ ）
A．
B．
C．
D． 
9．实数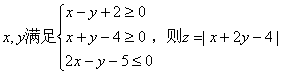
的最大值为 （ ）
A．18 B．19 C．20 D．21
|
的左、右焦点O为F1、F2，线段F1F2被抛物线
的焦点分成5:3两段，则离心率为 （ ）
A．
B．
C．
D．
|
A．α＜β＜γ＜δ B．β＜γ＜δ＜α C．α＜β＜δ＜γ D．β＜δ＜α＜γ
12．已知双曲线
的焦点分别为F1、F2，点P在双曲线上且PF1
=4PF2，则双曲线离心率的最大值为 （ ）
A．
B．
C．2 D．
二、填空题（本大题共4小题，每小题4分，共16分，把答案填在答题纸上）
13．一直线与一个正四棱柱各面所成角都为，则
.
14．平行四边形四个顶点A，B，C，D在平面同一侧，其中三点到距离为2、3、7，则顶点另一顶点到的距离为
.
|
上至少有三个不同点到直线l：ax + by = 0的距离为
，则直线l斜率范围
.
16．椭圆
的左右焦点分别为F1、F2，点P在椭圆上，若P，F1、F2是一个直角三角形的三个顶点，则P到X轴距离为
.
三、解答题（本大题共6小题，共74分，解答应写出文字说明，证明过程或演算步骤）
17．（12分）一束光线通过点M(25,18)射到x轴，被反射到圆C：
上，求通过圆心的反射线方程.
18．已知椭圆C：
，试确定m的取值范围，使得椭圆C上有两个不同的点关于直线l：y =
4x + m对称.
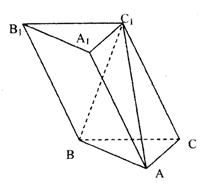
19．（12分）已知：在三棱柱ABC—A1B1C1中侧棱与底面成60°角，AB⊥AC，BC1⊥A1C1，AB=4，AC=3，
（1）求证：面ABC1⊥面ABC；
|
|
20．（12分）设双曲线C：
与直线l：
相交于不同的两点A、B
（1）求曲线C的离心率e的取值范围；
（2）设直线l与y轴交点为P，且
，求a的值.
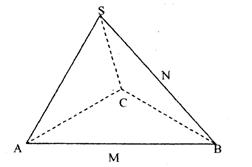
21．（12分）在三棱锥S—ABC中，△ABC是边长为4的正三角形，面SAC⊥ABC，SA=SC=
，M、N分别为AB、SB的中点，
|
（2）求二面角N—CM—B的正切值大小；
（3）求点B到面CMN的距离.
|
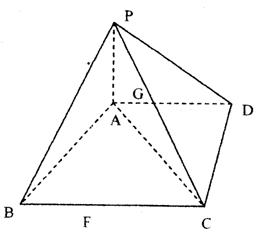
22．（14分）已知四棱锥P—ABCD中，PA⊥面ABCD，底面ABCD为直角梯形，∠ADC是直角，AD∥BC，AB⊥AC，G为△PAC的重心，F在线段BC上且CF=2FB
|
（2）证明：FG⊥AC.
山西省实验中学高三第五次月考
数学试题（文科）参考答案
|
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | D | D | C | B | B | B | D | D | D | D | D | B |
二、填空题（本大题共4小题，每小题4分，共16分，把答案填在答题纸上）
13． 14．6或8 15．
16．1或
(文:
)
三、解答题（本大题共6小题，共74分，解答应写出文字说明，证明过程或演算步骤）
17．（12分）x + y－7 = 0
18．（12分）
19．（12分）（1）略 （2）
20．（12分）（1）
（2）
21．（12分）（1）略 （2） （3）
22．（14分）略