湖南省常德市二中2007届高三最后一次模拟考试
数学试题(文史类)
一. 选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项正确,每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,多涂、不涂或涂错均得0分.
1.定义集合运算:A⊙B={![]() ,x∈A,y∈B},设集合A={
,x∈A,y∈B},设集合A={![]() ,0,1},B=
,0,1},B=
{![]() },则集合A⊙B的所有元素之和为
},则集合A⊙B的所有元素之和为
A.1 B。0
C。![]() D。
D。![]()
2.已知命题“若![]() ,则
,则![]() 且
且![]() ”。这个命题与它的否命题应当存在( )
”。这个命题与它的否命题应当存在( )
A、原命题是真命题,否命题是假命题; B、原命题与否命题都是真命题;
C、原命题是假命题,否命题是真命题; D、原命题与否命题都是假命题。
3. 已知数列![]() 是首项为
是首项为![]() ,公差为
,公差为![]() 的等差数列,若数列
的等差数列,若数列![]() 是等比数列,则其公比为( )
是等比数列,则其公比为( )
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
4.下列命题正确的是 ( )
A.函数![]() 在区间
在区间![]() 内单调递增
内单调递增
B.函数![]() 的最小正周期为
的最小正周期为![]()
C.函数![]() 的图像是关于点
的图像是关于点![]() 成中心对称的图形
成中心对称的图形
D.函数![]() 的图像是关于直线
的图像是关于直线![]() 成轴对称的图形
成轴对称的图形
5.设O为坐标原点,M(2,-1),如果点N(![]() ,
,![]() )满足
)满足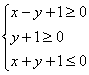 ,那么
,那么![]()
![]() 的最大值为
的最大值为
A. 2
B. 1
C. ![]() D.
D.![]()
6.若椭圆+y2=1(a>0)的一条准线经过抛物线y2=-8x的焦点,则该椭圆的离心率为
A. B. C. D.
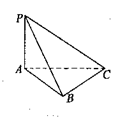 7.如图,三棱锥
7.如图,三棱锥![]() 中,
中,![]() 若三棱锥
若三棱锥![]() 的四个顶点在同一球面上,则这个球的表面积为
的四个顶点在同一球面上,则这个球的表面积为
A. ![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
8.连掷两次骰子分别得到点数m、n,则向量(m,n)与向量(-1,1)的夹角![]() 的概率是
的概率是
A.![]() B.
B.![]() C.
C. ![]() D.
D. ![]()
9.已知不等式![]() ,若对任意
,若对任意![]() 及
及![]() 该不等式恒成立,则实数
该不等式恒成立,则实数![]() 的取值范围是
( )
的取值范围是
( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
10. 某金店用一杆不准确的天平(两边臂不等长)称黄金,某顾客要购买![]() 黄金,售货员先将
黄金,售货员先将![]() 的砝码放在左盘,将黄金放于右盘使之平衡后给顾客;然后又将
的砝码放在左盘,将黄金放于右盘使之平衡后给顾客;然后又将![]() 的砝码放入右盘,将另一黄金放于左盘使之平衡后又给顾客,则顾客实际所得黄金
的砝码放入右盘,将另一黄金放于左盘使之平衡后又给顾客,则顾客实际所得黄金
A.大于![]() B.小于
B.小于![]() C.大于等于
C.大于等于![]() D.小于等于
D.小于等于![]()
二. 填空题:本大题共5小题,每小题5分,共25分,把答案填在答题卡中相应的横线上。
11.在![]() 中,
中,![]()
![]() ,
,![]() ,则
,则![]() 。
。
12.函数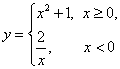 的反函数是
.
的反函数是
.
13.设![]() ,
则
,
则![]() =____________
=____________
14.若![]() 六个元素排成一列,要求
六个元素排成一列,要求![]() 不排在两端,且
不排在两端,且![]() 相邻,则不同的排法有_______________.种。
相邻,则不同的排法有_______________.种。
15.已知定义域为![]() 的函数
的函数![]() 对任意实数
对任意实数![]() 满足
满足![]() ,且
,且![]() ,给出下列结论:
,给出下列结论:
①![]() ;②
;②![]() 为奇函数;③
为奇函数;③![]() 是周期函数;④
是周期函数;④![]() 在
在![]() 内为单调函数
内为单调函数
其中正确的结论是 (填上所有正确结论的序号)
三. 解答题:本大题共6小题,共75分.解答应写出文字说明,证明过程或演算步骤.
16、(本小题满分12分)
在△ABC中,![]() 为三个内角
为三个内角![]() 为三条边,
为三条边,![]() 且
且![]()
(Ⅰ)判断△ABC的形状;
(Ⅱ)若![]() ,求
,求![]() 的取值范围.
的取值范围.
17. (本小题满分12分)
在军训期间,某校学生进行实弹射击.
(Ⅰ)通过抽签,将编号为1~6的六名同学排到1~6号靶位,试求恰有3名同学所抽靶位号与其编号相同的概率;
(Ⅱ)此次军训实弹射击每人射击三次,总环数不少于28环的同学可获得射击标兵称号.已知某同学击中10环、9环、8环的概率分别为0.1、0.2、0.2,求该同学能获得射击标兵称号的概率.
18.(本小题满分12分)
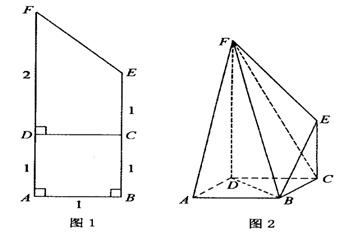
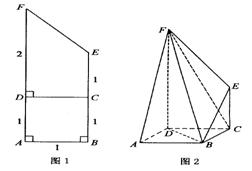
将如图1的直角梯形ABEF(图中数字表示对应线段的长度)沿直线CD折成直二面角,连结部分线段后围成一个空间几何体,如图2所示.
(1)求异面直线BD与EF所成角的大小;
(2)求二面角D—BF—E的大小;
(3)求F、A、B、C、D这五个点在同一球面上,求该球的表面积.
19.(本小题满分12分)
某地区的一种特色水果上市时间仅能持续![]() 个月,预测上市初期和后期会因供不应求使价格呈连续上涨态势,而中期又将出现供大于求使价格连续下跌,现有三种价格模拟函数.①
个月,预测上市初期和后期会因供不应求使价格呈连续上涨态势,而中期又将出现供大于求使价格连续下跌,现有三种价格模拟函数.① ![]() ; ②
; ② ![]() ;③
;③![]() .(以上三式中
.(以上三式中![]() 均为常数,且
均为常数,且![]() )。
)。
(1) 为准确研究其价格走势,应选哪种价格模拟函数,为什么?
(2) 若![]() ,求出所选函数
,求出所选函数![]() 的解析式(注:函数的定义域是
的解析式(注:函数的定义域是![]() ,其中
,其中![]() 表示
表示![]() 月
月![]() 日,
日,![]() 表示
表示![]() 月
月![]() 日,…,以此类推);
日,…,以此类推);
(3)为保证果农的收益,打算在价格下跌期间积极拓宽外销,请你预测该果品在哪几
个月份内价格下跌,以及在哪个月份内价格达到最高。
20.(本小题满分13分)
设![]() =
=![]() (a>0)为奇函数,且
(a>0)为奇函数,且![]() min=
min=![]() ,数列{an}与{bn}满足如下关系:a1=2,
,数列{an}与{bn}满足如下关系:a1=2,
![]() ,
,![]() .
.
(1) 求f(x)的解析表达式;
(2) 证明:当n∈N+时, 有bn![]()
![]() .
.
21.(本题满分14分)
已知焦点在x轴上的双曲线C的两条渐近线过坐标原点,且两条渐近线与以点![]() 为圆心,1为半径为圆相切,又知C的一个焦点与A关于直线y=x对称.
为圆心,1为半径为圆相切,又知C的一个焦点与A关于直线y=x对称.
(1)求双曲线C的方程;
(2)若Q是双曲线C上的任一点,F1、F2为双曲线C的左、右两个焦点,从F1引∠F1QF2的平分线的垂线,垂足为N,试求点N的轨迹方程.
(3)设直线y=mx+1与双曲线C的左支交于A、B两点,另一直线L经过M(-2,0)及AB的中点,求直线L在y轴上的截距b的取值范围.
常德市二中2007届高三模拟考试
数学试题参考答案(文史类)
说明:
1.本解答列出试题的一种或几种解法,如果考生的解法与所列解法不同,可参照解答中评分标准的精神进行评分。
2.评阅试卷,应坚持每题评阅到底,不要因为考生的解答中出现错误而中断对该题的评阅,当考生的解答在某一步出现错误,影响了后继部分,但该步以后的解答未改变这一题的内容和难度时,可视影响程度决定后面部分的给分,这时原则上不应超过后面部分应给分数之半,如果有较严重的概念性错误,就不给分。
一、选择题:(本小题满分50分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | B | C | C | A | B | D | A | D | C | A |
二、填空题:(本小题满分25分)
11. 1/2 12. 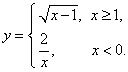 13. 128 14.144 15. (2)(3)
13. 128 14.144 15. (2)(3)
三、解答题
16.(本小题满分12分)
解:(1)由![]() 及正弦定理有:
及正弦定理有:![]() ……3分
……3分
∴![]() 或
或![]() …………4分
…………4分
若![]() ,且
,且![]() ,∴
,∴![]() ,
,![]() ; ……5分
; ……5分
∴![]() ,则
,则![]() ,∴
,∴![]() 三角形.
…………6分
三角形.
…………6分
(2)∵ ![]() ,∴
,∴![]() ,
…………8分
,
…………8分
∴![]() ,而
,而![]() ,
…………9分
,
…………9分
∴![]() ,
…………10分
,
…………10分
∴![]() ,
…………11分
,
…………11分
∴![]() .
…………12分
.
…………12分
17.(本小题满分12分)
解:(Ⅰ)设恰有3名同学所抽靶位号与其号码相同的事件为A,则事件A所包含的基本事件的种数为2C,而六名同学通过抽签排到1~6号靶位的排法种数为A.……3分
由于每位同学通过抽签排到某个靶位是等可能的,所以P(A)==.
答:恰有3名同学所抽靶位号与其号码相同的概率为.……………………………6分
(Ⅱ)设该同学恰好击中28环、29环、30环的事件分别为B,C,D, 他能获得射击标兵称号的事件为E,则事件B,C,D彼此互斥。
∵P(B)=C×(0.1)2×0.2+ C×0.1×(0.2)2=0.018,
P(C)=C×(0.1)2×0.2=0.006,
P(D)= (0.1)3=0.001,…………………………………………………………………9分
∴P(E)=P(B+C+D)=P(B)+P(C)+P(D)=0.018+0.006+0.001=0.025.
答:该同学能获得射击标兵称号的概率为0.025.……………………………………12分
18.(本小题满分12分)
解:∵平面ABCD⊥平面DCEF,ABCD为正方形,DCEF为直角梯形,
∴以DA所在直线为x轴、DC所在直线为y轴、DF所在直线为z轴建立空间直角坐标系![]() ,则
,则![]() …………1分
…………1分
(1)![]() …3分
…3分
∴异面直线AC与EF所成的角为![]() .
…………4分
.
…………4分
(2) ![]() ∴
∴![]()
∴平面BDF的法向量为![]() ,
…………5分
,
…………5分
又设平面BEF的法向量![]() ,
,
则由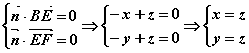 取
取![]()
∴平面BEF的法向量为![]() …………7分
…………7分
![]()
∴二面角![]() 的大小为
的大小为![]() …………8分
…………8分
(3)易知BF的中点H就是球心,HA=HB=HC=HD=HF=![]() …………11分
…………11分
∴![]() …………12分
…………12分
(其它方法请参照给分)
19.(本小题满分12分)
解:(Ⅰ)应选f(x)=x(x-q)![]() +p. ……………………………………………………………1分
+p. ……………………………………………………………1分
因为①f(x)=p·q![]() 是单调函数;
是单调函数;
②f(x)=px![]() +qx+1的图象不具有先升再降后升特征;
+qx+1的图象不具有先升再降后升特征;
③f(x)=x(x-q)![]() +p中,f′(x)=3x
+p中,f′(x)=3x![]() -4qx+q
-4qx+q![]() ,
,
令f′(x)=0,得x=q,x=![]() ,f(x)有两个零点.可以出现两个递增区间和一个递减区间.
,f(x)有两个零点.可以出现两个递增区间和一个递减区间.
……………………………………………………………………………………………4分
(Ⅱ)由f(0)=4,f(2)=6得:
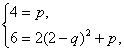 解之得
解之得![]() (其中q=1舍去).
(其中q=1舍去).
∴函数f(x)=x(x-3)![]() +4,即f(x)=x
+4,即f(x)=x![]() (0≤x<5)…………………8分
(0≤x<5)…………………8分
(Ⅲ)由![]() <0,解得1<x<3 ,
<0,解得1<x<3 ,
∴函数f(x)=x![]() 在区间(1,3)上单调递减,
在区间(1,3)上单调递减,
∴这种果品在5月,6月份价格下跌.
由![]() =0得:x=1 3
=0得:x=1 3
∵f(1)=8,f(3)=4,f(0)=4,f(5)=24
∴x=5 时,f(x)有最大值
即在9月份时,这种果品价格达到最大值。………………………………………………12分
20.(本小题满分13分)
解:(1)由f(x)是奇函数,得 b=c=0, ………… (3分)
由f(x)min=![]() ,得a=2,故f(x)=
,得a=2,故f(x)= ![]() …………
(6分)
…………
(6分)
(2) ![]() =
=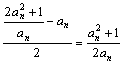 ,
,
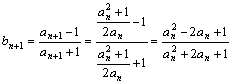 =
=![]() =
=![]() …………
(8分)
…………
(8分)
∴![]() =
=![]() =
=![]() =…=
=…=![]() ,而b1=
,而b1=![]()
∴![]() =
=![]() ………… (10分)
………… (10分)
当n=1时, b1=![]() ,命题成立,
…………
(11分)
,命题成立,
…………
(11分)
当n≥2时
∵2n-1=(1+1)n-1=1+![]() ≥1+
≥1+![]() =n
=n
∴![]() <
<![]() ,即
bn≤
,即
bn≤![]() .
………… (13分)
.
………… (13分)
21.(本题满分14分)
解:(1)设双曲线C的渐近线方程为y=kx,即kx-y=0
∵该直线与圆
![]() 相切,
相切,
∴双曲线C的两条渐近线方程为![]() …………2分
…………2分
故设双曲线C的方程为![]() ,又∵双曲线C的一个焦点为
,又∵双曲线C的一个焦点为![]()
∴![]() ,∴双曲线C的方程为
,∴双曲线C的方程为![]() ………4分
………4分
(2)若Q在双曲线的右支上,则延长QF2到T,使QT=OF1
若Q在双曲线的左支上,则在QF2上取一点T,使QT=QF1
根据双曲线的定义TF2=2,所以点T在以F2![]() 为圆心,2为半径的圆上,即点T的轨迹方程是
为圆心,2为半径的圆上,即点T的轨迹方程是![]() ①
…………6分
①
…………6分
由于点N是线段F1T的中点,设N(x,y),T(![]() )
)
则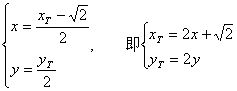
代入①并整理得点N的轨迹方程为 ![]() ………9分
………9分
(3)由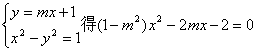
令![]()
直线与双曲线左支交于两点,等价于方程
![]() 上有两个不等实根.
上有两个不等实根.
因此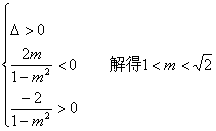 又AB中点为
又AB中点为![]()
∴直线L的方程为![]() …………12分
…………12分
令x=0,得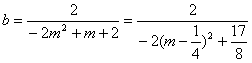
∵![]() ∴
∴![]()
∴故b的取值范围是![]() …………14分
…………14分