辽宁省部分重点中学协作体2007届高三模拟考试
数学试题（文科）
本试题分为第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分.共150分，考试时间120分钟.
第Ⅰ卷（选择题）
一、选择题：本大题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是最符合题目要求的。
1．若
，则下列选项正确的是 （ ）
A．0
M B．{0}∈M C．φ∈M D．{0}M
2．
的展开式中，各项系数和为 （ ）
A．1 B．2n C．－1 D．1或－1
3．{an}为等差数列，a10=33，a2=1，Sn为数列{an}的前n项和，则S20－2S10= （ ）
A．40 B．200 C．400 D．20
4．以下是立体几何中关于线、面的四个命题
（1）垂直于同一平面的两个平面平行
（2）若异面直线a、b不垂直，则过a的任何一个平面与b均不垂直
（3）垂直于同一平面的两条直线一定平行
（4）垂直于同一直线的两个平面一定平行
A．1 B．2 C．3 D．4
5．关于x的不等式ax+b<0的解集为{xx>1}，则关于x的不等式
的解集为（ ）
A．（1，2） B．（－1，2）
C．（－∞，－1）∪（2，+∞） D．（2，+∞）
6．函数
是函数
的反函数，若过点（1，0），则
的图像必过点 （ ）
A．（1，2） B．（－1，1） C．（1，1） D．（1，－1）
7．长方体ABCD—A1B1C1D1中，直线B1C和C1D与底面ABCD所成的角分别为60°和
45°，则异面直线B1C和C1D所成的角和余弦值为 （ ）
A．
B．
C．
D．
8．若
=
（ ）
A．
B．－ C．1 D．－1
9．已知
那么 （ ）
A．
B．
C．
D．
|
A．
B．
C．
D．
11．过双曲线
的左焦点F作倾斜角为60°的直线与双曲线相交于A、B两点，若
则双曲线的离心率e为 （ ）
A．
B．
C．或 D．以上答案都不对
12．
的取值范围为 （ ）
A．
B．
C．
D．
第Ⅱ卷（非选择题，共90分）
二、填空题：本大题共4小题，每小题4分，共16分。
13．已知x、y满足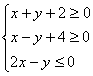
则z=2x+y的最大值为 .
14．已知中心在坐标原点的双曲线的一个焦点为（4，0），一条渐近线的方程为
，
则双曲线的方程为 .
15．正三棱锥P—ABC，PC⊥面PAB，PC=
，则过点P、A、B、C的球的体积为
.
16．把函数
的图象按向量
平移得函数
的图象，且
的坐标为
.
|
17．（本小题满分12分）
已知
（1）求f(x)的值域.
（2）求f(x)的单调递增区间.
18．（本小题满分12分）
甲、乙两个射手，各射击一次命中目标的概率分别为0.8、0.9
（1）甲、乙同时射击一个目标，求目标被击中的概率.
（2）甲、乙每人有三发子弹，两人各自独立地射击同一个目标，一直到子弹打光为止，求停止射击时目标被击中2次的概率.
|
19．（本小题满分12分）
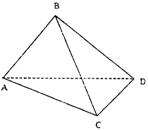
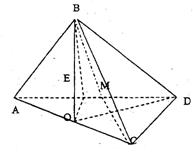
四面体ABCD中，已知AB⊥面BCD，AB=BC=2，
BD=2
，∠DBC=45°
（1）证明：CD⊥面ABC。
（2）求二面角B—AD—C的平面角的大小.
（3）若AD中点为M，求点A到面BMC的距离.
20．（本小题满分12分）
已知数列
（1）写出数列
的通项公式
.
（2）
，设数列
的前n项和为Sn，求Sn。
（3）设
，求数列
的最大项.
21．（本小题满分12分）
已知F为抛物线x2=2py(p>0)的焦点，过F作直线与抛物线交于A、B两点，以A、B为切点分别作抛物线的切线L1、L2，若L1与L2交于点P，求：
（1）点P的轨迹方程。
（2）若△PAB的面积的最小值为16，求抛物线的方程。
22．（本小题满分12分）
已知函数f(x)=x3+mx2+1
（1）求
的单调递减区间.
（2）若对任意
成立，求m的取值范围.
辽宁省部分重点中学协作体2007届高三模拟考试
数学试题（文科）参考答案
一、选择题
1．D 2．D 3．C 4．C 5．B 6．B 7．D 8．A 9．D 10．C 11．B 12．A
|
13．16 14．
15．
16．
三、解答题
17．解：
（1）
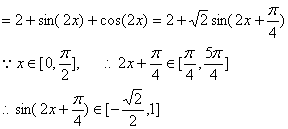
…………6分
（2）
的增区间为
…………12分
18．解：（1）∵目标不被击中的概率为0.1×0.2=0.02
∴目标被击中的概率为1－0.02=0.98 …………3分
（2）甲击中2次且乙没击中的概率为：
乙击中2次且甲没击中的概率为：
乙击中1次且甲击中1次的概率为：
…………9分
所以停止射击时目标被击中2次的概率为：
0.000384+0.001944+0.002592=0.00492 …………12分
19．解：（1）∵AB⊥面BCD ∴AB⊥CD
|
，∠DBC=45°
∴由余弦定理得CD=2 ∴∠BCD=90°
∴BC⊥CD
∴CD⊥面ABC…………4分
（2）由（1）知AC⊥CD
∵AD=
CD=2 ∴AC=
∵AB=BC=2 ∴取AC中点O，连接BO、DO
则BO⊥AC ∵面ABC⊥面ACD ∴BO⊥面ACD
过O作OE⊥AD于E，连接EB，则根据三垂线定理可得BE⊥AD
∴∠BEO为所求.
在△ABC中，BO=
AC=
在△ACD中，OE=AO×sin∠CAD=
在△AOE中，tan∠BEO=
∴
∴二面角B—AD—C的平面角的大小为
…………8分
（3）设A到面BMC的距离为h
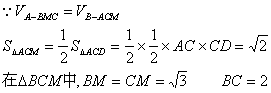
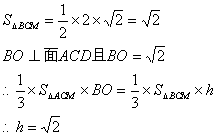
∴A到面BMC的距离为 …………12分
20．解：（1）
…………2分
（2）因为
所以
…………6分
（3）因为
所以当
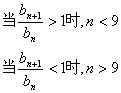
所以
…………10分
数列{
}的最大项为
…………12分
21．解：（1）
∴设直线AB的方程为
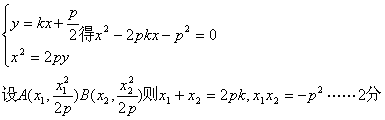
由
所以以A为切点的切线L1方程为
以B为切点的切线L2方程为
设交点P（x，y）
则可解得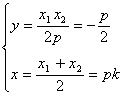
…………6分
所以点P的轨迹方程为
…………8分
（2）
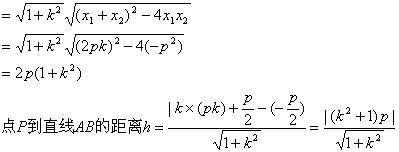
所以
的最小值为p2
…………11分
所以p2=16 p=4
∴抛物线方程为
…………13分
22．解：（1）
所以减区间为
所以减区间为
若m=0则因为
无解，所以无减区间 …………6分
（2）
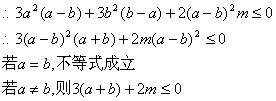
…………10分
…………3分