辽宁省部分重点中学协作体2007届高三模拟考试
数学试题（理科）
本试题分为第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分.共150分，考试时间120分钟.
第Ⅰ卷（选择题）
一、选择题：本大题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是最符合题目要求的。
1．若
，则下列选项正确的是 （ ）
A．0
M B．{0}∈M C．φ∈M D．{0}M
2．
= （ ）
A．10－2i B．10 C．10+2i D．8
3．{an}为等差数列，a10=33，a2=1，Sn为数列{an}的前n项和，则S20－2S10= （ ）
A．40 B．200 C．400 D．20
4．关于x的不等式ax+b<0的解集为{xx>1}，则关于x的不等式
的解集为（ ）
A．（1，2） B．（－1，2）
C．（－∞，－1）∪（2，+∞） D．（2，+∞）
5．
= （ ）
A．不存在 B．－
C． D．1
6．有以下四个命题 （ ）
（1）垂直于同一平面的两个平面平行
（2）若异面直线a、b不垂直，则过a的任何一个平面与b均不垂直
（3）假定一个总体由n个个体组成，现从中抽取一个容量为m的样本（0<m<n），则每一个个体被抽到的概率一定为
（4）
其中n∈N*
A．1 B．2 C．3 D．4
7．长方体ABCD—A1B1C1D1中，直线B1C和C1D与底面ABCD所成的角分别为60°和
45°，则异面直线B1C和C1D所成的角和余弦值为 （ ）
A．
B．
C．
D．
8．若
=
（ ）
A．
B．－ C．1 D．－1
9．已知
的最大值为 （ ）
A．1 B．2 C．3 D．4
|
A．
B．
C．
D．
11．过双曲线
的左焦点F作倾斜角为60°的直线与双曲线相交于A、B两点，若
则双曲线的离心率e为 （ ）
A．
B．
C．或 D．以上答案都不对
12．点O为△ABC内一点，且存在正数
，设△AOB，△AOC的面积分别为S1、S2，则S1：S2= （ ）
A．λ1：λ2 B．λ2：λ3 C．λ3：λ2 D．λ2：λ1
|
二、填空题：本大题共4小题，每小题4分，共16分。
13．已知x、y满足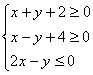
则z=2x+y的最大值为 .
14．正三棱锥P—ABC，PC⊥面PAB，PC=2
，则过点P、A、B、C的球的体积为
.
15．⊙A：(x－3)2+(y－5)2=1，⊙B:(x－2)2+(y－6)2=1，P是平面内一动点，过P作⊙A、⊙B的切线，切点分别为D、E，若
的最小值为
.
16．
，则a的取值范围为 .
三、解答题：本大题共6小题，共74分，解答应写出必要的文字说明、证明过程或演算步骤.
|
已知
（1）求f(x)的值域.
（2）求f(x)的单调递增区间.
18．（本小题满分12分）
甲乙两人独立解某一道数学题，已知该题被甲独立解出的概率为0.6，被甲或乙解出的概率为0.92。求：
（1）求该题被乙独立解出的概率。
（2）求解出该题的人数ξ的数学期望和方差。
|
19．（本小题满分12分）
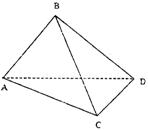
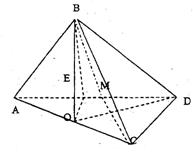
四面体ABCD中，已知AB⊥面BCD，AB=BC=2，
BD=2，∠DBC=45°
（1）证明：CD⊥面ABC。
（2）求二面角B—AD—C的平面角的大小.
（3）若AD中点为M，求点A到面BMC的距离.
20．（本小题满分12分）
已知F为抛物线x2=2py(p>0)的焦点，过F作直线与抛物线交于A、B两点，以A、B为切点分别作抛物线的切线L1、L2，若L1与L2交于点P，求：
（1）点P的轨迹方程。
（2）若△PAB的面积的最小值为16，求抛物线的方程。
21．（本小题满分12分）
已知函数f(x)=2x+alnx，
（1）若a<0，证明：对于任意两正数x1、x2，总有
成立。
（2）若存在x∈[1,e]，使不等式
成立，求a的取值范围.
22．（本小题满分14分）
已知数列
（1）求数列{
}的通项公式.
（2）设数列{}的前n项和为Sn，证明Sn<n－ln(n+1).
（3）设
，证明：对任意的正整数n、m，均有
.
辽宁省部分重点中学协作体2007届高三模拟考试
数学试题（理科）参考答案
一、选择题
1.D 2.B 3.C 4.B 5.C 6.B 7.D 8.A 9.B 10.C 11.B
|
二、填空题
13.16 14. 
15. 
16. 
三、解答题
17．解：
（1）
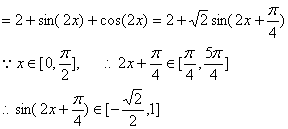
…………6分
（2）
的增区间为
…………12分
18．解：（1）记甲、乙分别解出此题的事件记为A、B.
设甲独立解出此题的概率为P1，乙独立解出此题的概率为P2.
则P（A）=P1=0.6，P（B）=P2
P（A+B）=1－P（
）
=1－(1－P1)(1－P2)=P1+P2－P1+P2=0.92
∴0.6+P2－0.6P2=0.92
则 0.4P2=0.32即P2=0.8.………………………………5分
（2）P（ξ=0）=P（
）·P（
）=0.4×0.2=0.08
P(ξ=1)=P(A)P()+P()P(B)=0.6×0.2+0.4×0.8=0.44
P(ξ=2)=P(A)·P(B)=0.6×0.8=0.48
ξ的概率分布为：
| ξ | 0 | 1 | 2 |
| P | 0.08 | 0.44 | 0.48 |
………………………………………………………………………………8分
Eξ=0×0.08+1×0.44+2×0.48=0.44+0.96=1.4…………………………10分
Dξ=(0－1.4)2·0.08+(1－1.4)2·0.44+(2－1.4)2·0.48
=0.1568+0.0704+0.1728=0.4
∴解出该题的人数ξ的数学期望为1.4，方差为0.4。………………12分
19．解：（1）∵AB⊥面BCD ∴AB⊥CD
|
，∠DBC=45°
∴由余弦定理得CD=2 ∴∠BCD=90°
∴BC⊥CD
∴CD⊥面ABC…………4分
（2）由（1）知AC⊥CD
∵AD=
CD=2 ∴AC=
∵AB=BC=2 ∴取AC中点O，连接BO、DO
则BO⊥AC ∵面ABC⊥面ACD ∴BO⊥面ACD
过O作OE⊥AD于E，连接EB，则根据三垂线定理可得BE⊥AD
∴∠BEO为所求.
在△ABC中，BO=AC=
在△ACD中，OE=AO×sin∠CAD=
在△AOE中，tan∠BEO=
∴
∴二面角B—AD—C的平面角的大小为
…………8分
（3）设A到面BMC的距离为h
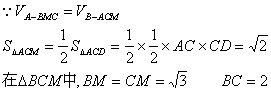
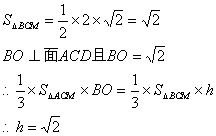
∴A到面BMC的距离为 …………12分
20．解：（1）
∴设直线AB的方程为
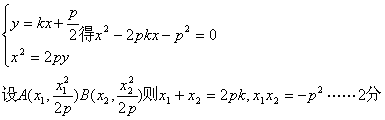
由
所以以A为切点的切线L1方程为
以B为切点的切线L2方程为
设交点P（x，y）
则可解得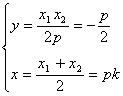
所以点P的轨迹方程为
…………8分
（2）
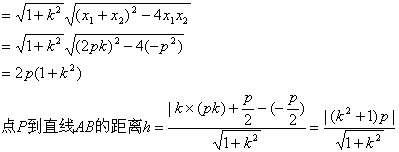
所以
的最小值为p2…………10分
所以p2=16 p=4
∴抛物线方程为
…………12分
21．解：（1）
|
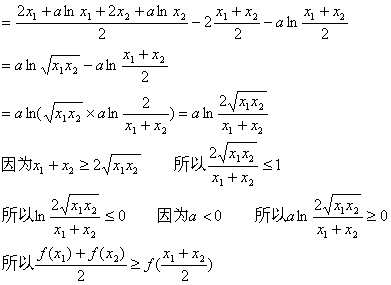
（2）因为存在x∈[1，e]使不等式成立
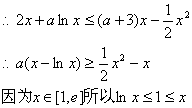
并且等号与不同时取到，所以lnx<x，即x－lnx>0
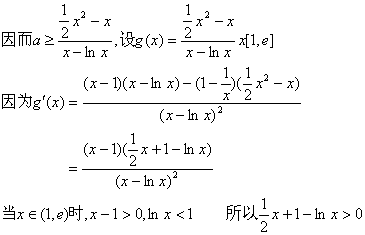
所以g′(x)>0，又因为g(x)在x=1和x=e处连续，
所以g(x)在x∈[1，e]时为增函数，因而g(x)≥g(1)=－
所以a≥－………………………………………………12分
22．解：（1）因为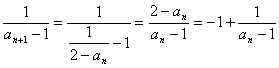
|
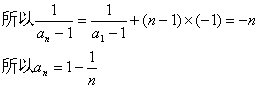
（2）设F(x)=ln(x+1)－x(x>0)
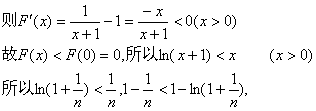
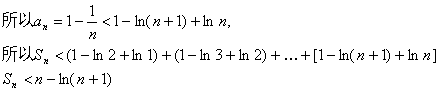
（3）因为
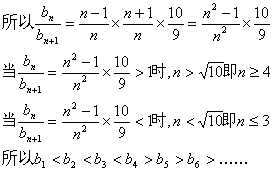
又因为n≥2时，bn>0，并且b1=0，所以
.
所以对任意的正整数n、m，均有bn－bm的最大值为：
=
所以对任意的正整数n、m，均有………………14分