山东省枣庄市2007届高三第三次调研考试
数学试题(理工农医类)
本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.共150分,考试时间120分钟.
第I卷(选择题,共60分)
注意事项:
1.答第I卷前,考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上。
2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡
皮擦干净后,再选涂其它答案标号。不能答在试卷上。
3.考试结束,监考人将本试卷和答题卡一并收回.
参考公式:
如果事件A、B互斥,那么 正棱锥、圆锥的侧面积公式
P(A+B)=P(A)+P(B)
![]()
如果事件A、B相互独立,那么
P(A·B)=P(A)·P(B) 其中c表示底面周长,l表示斜高或母线长
如果事件A在一次试验中发生的概率是 球的体积公式
P,那么n次独立重复试验中恰好发生k
![]() ,
,
如果事件A在一次试验中发生的概率是P,
那么n次独立重复试验中恰好发生k次 其中R表示球的半径.
的概率
![]()
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是最符合题目要求的.
1.![]() 的共轭复数是 ( )
的共轭复数是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.已知条件p:1≤x≤4,条件q:x-2>1,则p是![]() q的 ( )
q的 ( )
A.充分不必要条件 B.必要不充分条件
|
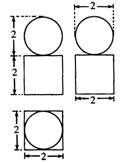
3.一个几何体的三视图如图所示,则该几何体的体积等于 ( )
A.8+![]()
B.4+![]()
C.8+4π
D.![]()
4.某种动物由出生算起活到10岁的概率为0.9,活到15岁的概率为0.6,现有一个10岁的这种动物,它能活到15岁的概率是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.设F是椭圆![]() 的右焦点,椭圆上的点与点F的最大距离为M,最小距离是m,
的右焦点,椭圆上的点与点F的最大距离为M,最小距离是m,
则椭圆上与点F的距离等![]() (M+m)的点的坐标是 ( )
(M+m)的点的坐标是 ( )
A.(0,±2) B.(0,±1) C.![]() D.
D.![]()
|
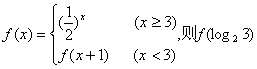 的值是 ( )
的值是 ( )
A.![]() B.
B.![]()
C.24 D.12
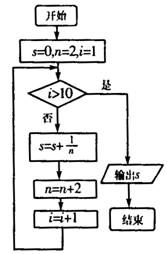
7.如图,程序框图所进行的求和运算是 ( )
A.![]()
B.![]()
C.![]()
D.![]()
8.设双曲线x2-y2=1的两条渐近线与直线x=![]() 围成的三角形区域(包含边界)为D,P
围成的三角形区域(包含边界)为D,P
(x,y)为D内的一个动点,则目标函数z=x-2y的最小值为 ( )
A.-2 B.-![]() C.0 D.
C.0 D.![]()
9.设α、β、γ为平面,a、b为直线,给出下列条件:
①a![]() α、b
α、b![]() β,a//β,b//α; ②α//γ,β//γ;
β,a//β,b//α; ②α//γ,β//γ;
③α⊥γ,β⊥γ; ④a⊥α,b⊥β,a//b.
其中能使α//β成立的条件是 ( )
A.①② B.②③ C.②④ D.③④
|
| x | 1 |
|
| f(x) | 1 |
|
则不等式f(x)≤2的解集是 ( )
A.{x0<x≤![]() } B.{x0≤x≤4}
} B.{x0≤x≤4}
C.{x-![]() ≤x≤
≤x≤![]() } D.{ x-4≤x≤4}
} D.{ x-4≤x≤4}
|
12.已知![]() ,且对任意
,且对任意![]() 都有
都有
①f(m,n+1)=f(m,n)+2; ②f(m+1,1)=2f(m,1).则f(2007,2008)的值为 ( )
A.22006+2007 B.22007+2007 C.22006+4014 D.22007+4014
|
二、填空题:本大题共4小题,每小题4分,共16分,把答案填在题中横线上.
13.若点![]() 的弦AB的中点,则地线AB的方程是
.
的弦AB的中点,则地线AB的方程是
.
14.在代数式![]() 的展开式中,常数项是
.
的展开式中,常数项是
.
15.在样本的频率分布直方图中,共有4个长方形,这4个小方形的面积由小到大构成等差数列{an},已知a2 = 2a1,且样本容量为400,则小长方形面积最大的一组的频数为 .
16.对于函数![]() 给出下列四个命题:
给出下列四个命题:
①该函数是以π为最小正周期的周期函数;
②当且仅当x = π+ kπ(k∈Z)时,该函数取得最小值-1;
③该函数的图象关于![]() (k∈Z)对称;
(k∈Z)对称;
④当且仅当![]() (k∈Z)时,
(k∈Z)时,![]()
其中正确合题的序号是 (请将所有正确命题的序号都填上)
三、解答题:本大题共6小题,共74分.解答应写出文字说明,证明过程或演算步骤.
17.(本小题满分12分)
在△ABC中,a、b、c分别是角A、B、C的对边,若向量![]() 的夹角为
的夹角为![]()
(I)求角B的大小;
(II)若![]() ,求a + c的最大值.
,求a + c的最大值.
18.(本小题满分12分)
已知数列{an}的前n项和为Sn,对一切正整数n,点![]() 都在函数
都在函数![]() 的图象上.
的图象上.
(I)求数列{an}的通项公式;
(II)设![]() ,求数列{bn}的前n和Tn.
,求数列{bn}的前n和Tn.
|
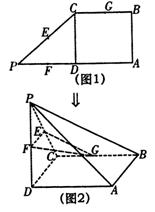
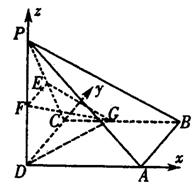
如图1,在直角梯形ABCP中,AP∥BC,AP⊥AB,
AB=BC=![]() AP=2,D为AP的中点,E,F,G分别为PC、
AP=2,D为AP的中点,E,F,G分别为PC、
PD、CB的中点,将△PCD沿CD折起,使点P在平面
ABCD内的射影为点D,如图2.
(I)求证:AP∥平面EFG;
(II)求二面角E—FG—D有一个三角函数值.
|
20.(本小题满分12分)
某次象棋比赛的决赛在甲乙两名棋手之间举行,比赛采用积分制,比赛规则规定赢一局得2分,平一局得1分,输一局得0分,比赛共进行五局,积分有超过5分者比赛结束,否则继续进行,根据以往经验,每局甲赢的概率为![]() ,乙赢的概率为
,乙赢的概率为![]() ,且每局比赛输赢互不影响,若甲第n局赢、平、输的得分分别记为an=2、an=1、an=0、n∈N*,
,且每局比赛输赢互不影响,若甲第n局赢、平、输的得分分别记为an=2、an=1、an=0、n∈N*,
1≤n≤5,令![]()
(I)求S3 = 5的概率;
(II)若随机变量ξ满足Sξ= 7(ξ表示局数),求ξ的分布列和数学期望.
21.(本小题满分12分)
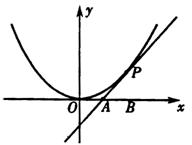
如图,已知直线l与抛物线![]() 相切于点P(2,1),且与x轴交于点A,O为坐标原点,定点B的坐标为(2,0).
相切于点P(2,1),且与x轴交于点A,O为坐标原点,定点B的坐标为(2,0).
(I)若动点M满足![]() ,求点M的轨迹C;
,求点M的轨迹C;
|
22.(本小题满分14分)
设![]() (e为自然对数的底数)
(e为自然对数的底数)
(I)求p与q的关系;
(II)若![]() 在其定义域内为单调函数,求p的取值范围;
在其定义域内为单调函数,求p的取值范围;
(III)证明:
①![]() ;
;
②![]() (n∈N,n≥2).
(n∈N,n≥2).
山东省枣庄市2007届高三第三次调研考试
数学试题(理工农医类)参考答案
一、选择题:本题考查基本知识和基本运算,每小题5分,共60分.
|
二、填空题:本题考查基本知识和基本运算,每小题4分,共16分.
13.![]() 14.-23 15.160 16.③④
14.-23 15.160 16.③④
三、解答题:本大题共6小题,共74分.
17.(本小题满分12分)
解:(I)由题意得
![]() ,………………………………2分
,………………………………2分
即![]() ,
, ![]() ,
,
![]() , ………………………………………………………… 4分
, ………………………………………………………… 4分
![]() (舍去),……………………………………………… 5分
(舍去),……………………………………………… 5分
![]() ………………………………………………………… 6分
………………………………………………………… 6分
(II)由(I)知![]()
而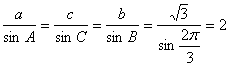 ,……………………………………………7分
,……………………………………………7分
![]() ………………………………………………………… 8分
………………………………………………………… 8分
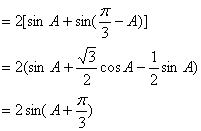
![]() ,
,
![]() …………………………………………………………………10分
…………………………………………………………………10分
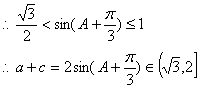
所以,a + c的最大值为2. ……………………………………………………………12分
18.(本小题满分12分)
解:(I)由题意,![]() ,
,
![]() ,…………………………………… 3分
,…………………………………… 3分
当![]() ,也适合上式,
,也适合上式,
∴数列{an}的通项公式为![]() ………………………………………5分
………………………………………5分
(II)![]()
![]() ①
①
![]() ② ………………7分
② ………………7分
②-①得,
![]() ………………………………8分
………………………………8分
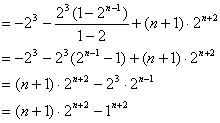
![]() …………………………………………………………………………12分
…………………………………………………………………………12分
19.(本小题满分12分)
解:由题意,△PCD折起后PD⊥平面ABCD,四边形ABCD是边长为2的正方形,PD=2.
(I)∵E、F、G分别为PC、PD、BC的中点.
∴EF∥CD,EG∥PB.
又CD∥AB ∴EF∥AB,PB∩AB = B,…………………………………………… 3分
∴平面EFG∥平面PAB.
|
(II)建立空间直角坐标系D—xyz,如图,则
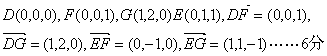
设平面DFG的法向量![]() ,
,
则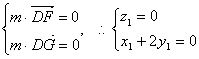 ,
,
令![]() ………………………………………………………………8分
………………………………………………………………8分
设平面EFG的法向量为![]() ,
,
则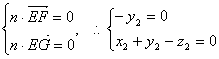 ,
,
令![]() , ………………………………………………………………10分
, ………………………………………………………………10分
![]()
设二面角E—FG—D为θ,则![]() ,
,
所以二面角E—FG—D的余弦值为![]() …………………………………………12分
…………………………………………12分
20.(本小题满分12分)
解:(I)S3 = 5,即前3局甲2胜1平. ………………………………………………1分
由已知甲赢的概率为![]() ,平的概率为
,平的概率为![]() ,输的概率为
,输的概率为![]() ,…………………………2分
,…………………………2分
得S3 = 5的概率为![]() …………………………………………………5分
…………………………………………………5分
(II)![]() ,且最后一局甲赢, ……………………………………… 6分
,且最后一局甲赢, ……………………………………… 6分
![]() ; ……………………………………………………8分
; ……………………………………………………8分
![]()
ξ的分布列为
| ξ | 4 | 5 |
| Pξ |
|
|
…………………………………10分
![]() ……………………………………………………12分
……………………………………………………12分
21.(本小题满分12分)
解:(I)由![]() ,
, ![]()
∴直线l的斜率为![]() , …………………………………………………………1分
, …………………………………………………………1分
故l的方程为![]() ,
,
∴点A坐标为(1,0) ……………………………………………………………… 2分
设![]() 则
则![]() ,
,
由![]() 得
得
![]()
整理,得![]() ………………………………………………………………4分
………………………………………………………………4分
∴动点M的轨迹C为以原点为中心,焦点在x轴上,长轴长为![]() ,短轴长为2的椭圆 …………………………………………………………………………………… 5分
,短轴长为2的椭圆 …………………………………………………………………………………… 5分
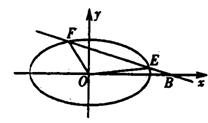
(II)如图,由题意知直线l的斜率存在且不为零,设l方程为y=k(x-2)(k≠0)①
|
![]() ,
,
由△>0得0<k2<![]() . 设E(x1,y1),F(x2,y2)
. 设E(x1,y1),F(x2,y2)
则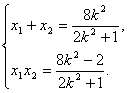 ②………………………………………………………7分
②………………………………………………………7分
令![]() ,
,
由此可得![]()
由②知![]()
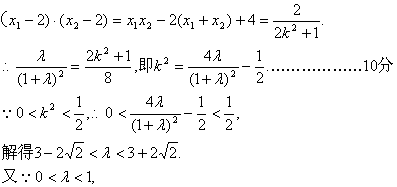
![]() .
.
∴△OBE与△OBF面积之比的取值范围是(3-2![]() ,1).………………12分
,1).………………12分
22.(本小题满分14分)
解:(I)由题意![]()
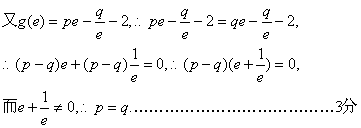
(II)由(I)知:![]()
![]()
令h(x)=px2-2x+p.要使g(x)在(0,+∞)为单调函数,只需h(x)在(0,+∞)满足:
h(x)≥0或h(x)≤0恒成立.………………………………4分
①![]() ,
,
![]()
∴g(x)在(0,+∞)单调递减,
∴p=0适合题意.………………………………………………5分
②当p>0时,h(x)=px2-2x+p图象为开口向上抛物线,
称轴为x=![]() ∈(0,+∞).
∈(0,+∞).
∴h(x)min=p-![]() .
.
只需p-![]() ≥0,即p≥1时h(x)≥0,g′(x) ≥0,
≥0,即p≥1时h(x)≥0,g′(x) ≥0,
∴g(x)在(0,+ ∞)单调递增,∴p≥1适合题意.…………………………7分
③当p<0时,h(x)=px2-2x+p图象为开口向下的抛物线,
其对称轴为x=![]()
![]() (0,+∞),
(0,+∞),
只需h(0)≤0,即p≤0时h(0)≤(0,+ ∞)恒成立.
∴g′(x)<0 ,∴g(x)在(0,+ ∞)单调递减,
∴p<0适合题意.
综上①②③可得,p≥1或p≤0.……………………………………9分
(III)证明:①即证:lnx-x+1≤0 (x>0),
设![]() .
.
当x∈(0,1)时,k′(x)>0,∴k(x)为单调递增函数;
当x∈(1,∞)时,k′(x)<0,∴k(x)为单调递减函数;
∴x=1为k(x)的极大值点,
∴k(x)≤k(1)=0.
即lnx-x+1≤0,∴lnx≤x-1.………………………………11分
②由①知lnx≤x-1,又x>0,
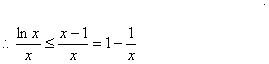

∴结论成立.…………………………………………………………………………14分