高三第三次质量检测数学试题
注意事项
考生在答题前请认真阅读本注意事项及各题答题要求:
1．本试卷共4页，包含选择题(第1题～第10题，共10题)、填空题(第11题～第16题共6题)、解答题(第17题～第21题，共5题)三部分。本次考试时间为120分钟,考试结束后，请将本试卷和答题卡一并交回。
2．答题前，请您务必将自己的姓名、考试证号用书写黑色字迹的0．5毫米签字笔填写在试卷及答题卡上。
3．作答非选择题必须用书写黑色字迹的0．5毫米签字笔写在答题卡上的指定位置，在其它位置作答一律无效。作答选择题必须用2B铅笔把答题卡上对应题目的答案标号涂黑。如需改动，请用橡皮擦干净后，再选涂其它答案。．
4．如有作图需要，可用2B铅笔作答，并请加黑加粗，描写清楚。
一、选择题：本大题共10小题。每小题5分．共50分,在每小题给出的四个选项中恰有一项是符合题目要求的.
1．函数y=sinx(x∈R)图象的对称轴方程中有一个是
A．x=0 B．x=
C．x=
D．x=2
2．圆(x-1)2 +(y+2)2=9截y轴所得的弦长为
A．
B．2
C．2
D．4
3．方程2x+x-4=O的解所在区间为
A．(-1，0) B．(0，1) C．(1，2) D．(2，3)
4．在(x－1)(x+1)6的展开式中x3的系数是
A．-5 B．5 C．-35 D.35
5．在等差数列
中，
≠0，当n≥2时，
－
+
=0,若
=46，则n的值为
A．23 B．24 C．11 D.12
6．已知扇形的面积为25，则该扇形周长的最小值为
A．20 B．10 C．10
D.5
7．在△ABC中，a，b，c分别是∠A，∠B，∠C的对边，已知a-b=c·cosB—c·cosA，则
△ABC的形状是
A．等腰三角形 B．直角三角形 C．正三角形 D．等腰三角形或直角三角形
8．从1，2，3，…，20这20个数中任取2个不同的数，则这两个数之和是3的倍数的概率为
A．
B．
C．
D．
9．已知球O是棱长为12的正四面体S-ABC的外接球，D，E,F分别是棱SA，SB，SC的
中点，则平面DEF截球O所得截面的面积是
A．36
B．40
C．48
D．54
10．椭圆
的左、右焦点分别为F1,F2 ,弦AB过F1
，若△ABF2的内切圆周长为
，A,B两点的坐标分别为(x1，y1)和(x2，y2)，则 y2－y1的值为
A．
B．
C．
D．
二、填空题：本大题共6小题，每小题5分,共30分,不需要写出解答过程,请把答案直接填写在答题卡相应位置上．
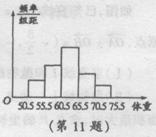
11．为了解高三学生的身体状况。抽取了部分男生的体重，将
所得的数据整理后，画出了频率分布直方图(如图)，已知
图中从左到右的前3个小组的频率之比为1︰2︰3，第4组
与第5组的频率分别为0.1875和0.0625，第2组的频数为
12，则抽取的男生人数是 ．
12．已知向量
，
满足=3， =4， 与的夹角是
，
则+2 =
．
13．在如图所示的九宫格中，用红、黄、蓝三种颜色涂其中三格，每种颜色
只涂一格，且红色不与另外两种颜色相邻(有公共边的方格称为相邻)，则不
同的涂法种数为 ．(用数字作答)
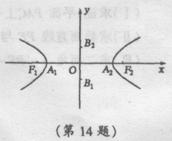14．如图，已知双曲线
的实轴为A1A2，虚轴为B1B2，
将坐标系的左半平面沿y轴折起，使双曲线的左焦点F1折至
F点，若F在平面A2B1B2内的射影恰好是双曲线的右顶点，
则直线B2F与平面A2B1B2所成角的正切值为 ．
15．已知方程lg(x－1)+lg(5－x)=lg(a－x)有两个不同的实数解，则实数a的取值范围是： ．
16．已知函数f(x)=
，g(x)=ax2－2
x +l(
∈Z，b∈N)．若存在
使，f()是f(x)的最大值，g()是g(x)的最小值，则满足条件的所有实数对(，b)
为 ．
三、解答题：本大题共5小题，共70分．请在答题卡指定区域内作答．解答时应写出文字说明、证明过程或演算步骤．
17．(本小题满分12分，第一小问、第二小问各6分)
已知函数f(x)=cos4x+2
sinxcosx－sin4x．
(I)求f(x)的最小正周期；
(Ⅱ)若x∈[0,]，求f(x)的最大值、最小值．
18．(本小题满分14分，第一小问8分，第二小问6分)
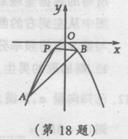
如图，已知直线l：y=kx－1与抛物线C：x2=－2py(p＞0)交于A,B两点，0为坐标原点
.
(I)求直线l和抛物线C的方程；
(Ⅱ)抛物线上一动点P从A到B运动，当△ABP面积最大时，求点P的坐标．
19．(本小题满分14分，第一小问、第二小问各4分，第三小问6分)
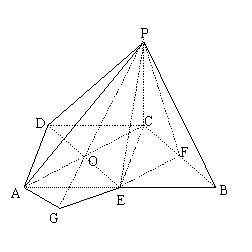
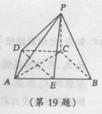如图，在四棱锥P—ABCD中，底面ABCD是直角梯形，∠ADC=，AB∥CD，
PC⊥面ABCD，PC=AD=DC=
AB，E为线段AB的中点．
(I)求证：平面PAC⊥平面PDE；
(Ⅱ)求异面直线PE与AC所成角的大小；
(Ⅲ)求二面角A一PE—D的大小．
20．(本小题满分14分，第一小问2分，第二小问、第三小问各6分)
已知函数f(x)=
，设正项数列满足
=l，
．
(I)写出
，
的值;
(Ⅱ)试比较与
的大小，并说明理由；
(Ⅲ)设数列
满足
=－，记Sn=
．证明：当n≥2时,Sn＜
(2n－1)．
21．(本小题满分16分，第一小问、第二小问各4分，第三小问8分)
已知函数f(x)=x3－3ax(a∈R)．
(I)当a=l时，求f(x)的极小值；
(Ⅱ)若直线菇x+y+m=0对任意的m∈R都不是曲线y=f(x)的切线，求a的取值
范围；
(Ⅲ)设g(x)=f(x)，x∈[－l，1]，求g(x)的最大值F(a)的解析式．
高三第三次质量检测数学试题
数学参考答案及评分标准
说明：
1、 本解答仅给出了一种解法供参考，如果考生的解法与本解答不同，可根据试题的主要考查内容对照评分标准制定相应的评分细则。
2、 评阅试卷，应坚持每题评阅到底，不要因为考生的解答中出现错误而中断对该题的评阅，当考生的解答在某一步出现错误时，如果后续部分的解答未改变该题的内容和难度，可视影响的程度决定后续部分的给分，但不得超过该部分正确解答应得分数的一半，如果后续部分的解答有较严重的错误，就不给分。
3、 解答右端所注分数，表示考生正确做到这一步应得的累加分数。
4、 给分或扣分以1分为单位，选择题和填空题不给中间分。
一、选择题：本题考查基本知识和基本运算。每小题5分，满分50分。
1．B 2．D 3．C 4．A 5．D 6．A 7．D 8．C 9．C 10．A
二、填空题：本题考查基本知识和基本运算。每小题5分，满分30分。
11．48； 12．7； 13．212； 14．
； 15．
； 16．（2，3）
三、解答题
17．(1)
……………………………………………………………2分
………………………………………………………………4分
所以
………………………………………………………………………6分
(2)因为
…………………………………………………8分
所以
…………………………………………………………10分
所以
的最大值为2,最小值为-1. ……………………………………………12分
18．由
得,
设
则
…………………………………2分
因为
=
……………………………………………………………4分
所以
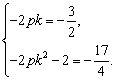解得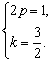 
…………………………………………………6分
所以直线
的方程为
抛物线C的方程为
…………………………8分
（2）方法一：由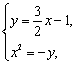
得，
设
………10分
因为
为定值，当
到直线的距离
最大时，△ABP的面积最大，
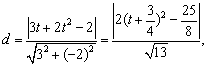…………………………………………………………12分
因为
所以当
时，最大，
此时
……………………………………………………………………………14分
方法二：设
依题意，抛物线过P的切线与平行时，△APB面积最大，…10分
，所以
…………………………………………………………12分
所以………………………………………………………14分
19．(1)
且E是AB的中点，而
所以
且
，所以四边形
是
平行四边形，又
，所以四边形是菱形，所以
，………………………… 2分
因为
平面
，DE
平面
所以
，所以
平面
，
又
平面
，
故平面
平面.………………… 4分
(2)取
的中点F，连结EF，则
，
所以
（或其补角）是异面直线
与
AC所成的角.……………………………….6分
连结
，因为
，所以
，又平面，所以
故
平面
，
平面 所以
设
，则
，在Rt△PFE中，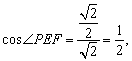
即异面直线与
所成的角为
.…………………………8分
(3)设
连结
，过
作
交的延长线于
，
由（1）知 平面平面，
连结
因为
所以
，……………………………………………… 11分
所以
是二面角A－PE－D的平面角设
因为Rt△
∽Rt△
，所以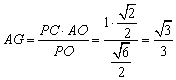
,
在Rt△AEG中，
所以
.
所以二面角A－PE－D的大小为
.……………………………………………16分
20．(1)
，因为
所以
………………………………
2分
（2）因为
所以
…………………………………3分
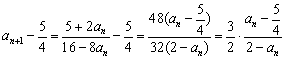,……………………………………………5分
因为
所以
与
同号，………………………………………………6分
因为
，
…，
即
……………………………………………………………………8分
（3）当
时，
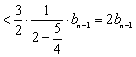，……………………………………………………………………10分
所以
，……………………………………………12分
所以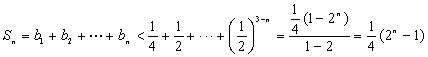
…………14分
21．（1）∵当a=1时
，令
=0，得x=0或x=1………………………2分
当
时
，当
时
∴在
上单调递减，在
上单调递增，
∴的极小值为
=-2.………………………………………………………………4分
（2）∵
………………………………………………………………6分
∴要使直线
=0对任意的
总不是曲线
的切线，当且仅当-1<-3a,
∴
.…………………………………………………………………………………………8分
(3)因
在[-1,1]上为偶函数,故只求在 [0,1]上最大值，…………9分
① 当
时，
，在
上单调递增且
,
∴
，∴
.…………………………………………10分
② 当
时 
i .当
，即
时
，
在上单调递增，此时
……………………………………………………………………12分
ii. 当
，即
时，
在
上单调递减，在
上单调递增.
10 当
即
时，在上单调递增，在上单调递减，故
.……………………………………14分
20当
即
时，
（ⅰ）当
即
时，
（ⅱ）
当
即
时，
综上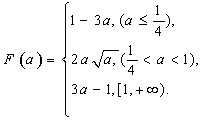
………………………………………………