昭通明达中学高三数学测试
姓名_________.
一、选择题：本大题共10小题，每小题5分，共50分。在每小题给出的四个选项中，只有一项是符合题目要求的。
1．设全集
，集合
，M={3,5},则集合
等于
( ）
A．
B．
C．
D．
2．在等差数列
中，
，则
（ ）
A．24 B．
3．已知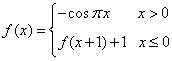
，则
的值等于
( ）
A．
B．
4．设
、
、
、
是满足条件+=+的任意正整数，则对各项不为0的数列，
是数列{
}为等比数列的
( ）
A．充分不必要条件 B．必要不充分条件
C．充要条件 D．既不充分也不必要条件
|
|
| 0 |
|
| 0.592 | 1 |
5．若指数函数
的部分对应值如右表：
则不等式
的解集为 （ ）
A．
B．
C．
D．
6．若函数
的图象的相邻两条对称轴的距离是
，则
的值为
( )
A．
B．
C．1
D．2
7．已知正方形ABCD边长为1, =,= ,= 则++的模等于 ( )
A.0
B
8．设函数
，则
（ ）
A．在区间
上是增函数 B．在区间
上是减函数
C．在区间
上是增函数
D．在区间
上是减函数
9．9.设=(cosα,sinα),=( cosβ, sinβ),则3-4的最大值是( )
A.49
B
10．已知函数
的图象与函数
的图象关于直线
对称，则
的值为 ( )
A．1 B．
C．2 D．
二、填空题：本大题共5小题，每小题5分，共25分，把答案填写在题中的横线上。
11．函数
的定义域是_______________
12．已知
、
均为锐角，且
，则
________
13．设数列的前项和为
，且
，则
_____
14．将函数
的图象上每一点的纵坐标不变，横坐标变为原来的
倍，得到图象C，若将的图象向上平移2个单位，也得到图象C，则
_______
15．若=(0,1), =(3,4)且向量k+与-k垂直,向量与k(+)同向, =(-3,2),则k等于___________.
三、解答题：本大题共6个小题，共75分。解答应写出文字说明、证明过程或演算步骤。
16．（本小题满分12分） 在
中，
、
、
分别是三内角A、B、C的对应的三边，已知
。
（Ⅰ）求角A的大小：
（Ⅱ）若
，判断的形状。
17．（本小题满分12分）
.设向量=(cos230,cos670), =(cos680,cos220), =+t(t∈R)
(1) 求· (2).求的最小值
18．（本小题满分12分）
在数列中，
，且满足
。
（Ⅰ）求数列的通项公式；
（Ⅱ）设
，求；
19．（本小题13分）
(1).在△ABC中已知sinA:sinB:sinC=3:5:7,求此三角形的最大内角的度数.
(2).在△ABC中,已知4sinBsinC=1,b2+c2-a2=bc,且B>C,求A,B,C.
20.求函数y=sin4x+2sinxcosx-cos4x的最小正周期和最小值,并写出该函数在[0, π]上的单调增区间.
昭通明达中学高三数学测试
姓名_________.
一、选择题：本大题共10小题，每小题5分，共50分。在每小题给出的四个选项中，只有一项是符合题目要求的。
1． a、b为实数，集合
表示把集合M中的元素x映射到集合N中仍为x，则
A．1 B．0 C．－1 D．±1
2． 设
是定义在R上的单调递减的奇函数，若
则
A . 
B. 
C. 
D. 
3．若一系列函数的解析式相同，值域相同，但定义域不同，称这些函数为—同族函数。那么，函数的解析式为
，值域为
的同族函数共有
A. 7个 B. 8个 C. 9个 D.10个
4．将函数
的图像按
平移之后得到函数
的图像,若
则
的值为
A． 
B
. 
C .
D . 或
5．在 中，若对任意
，则有
A．
B．
C. 
D.
6．若
(
)
A.关于直线y=x对称 B.关于x轴对称 C.关于y轴对称 D.关于原点对称
7．不等式
的解集为 （ ）
A．
B．
C．
D．
8．若a, b是非零向量且满足: (a –2b)^ a ，(b –2a)^ b ，则a与b的夹角是
(A)
(B)
(C)
(D)
9．把点(3，4)按向量
平移后的坐标为(－2，1)，则y＝2x的图象按向量平移后的图象的函数表达式为
A．y＝2x－5＋3 B．y＝2x－5－3 C．y＝2x＋5＋3 D．y＝2x＋5－3
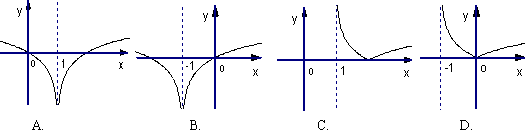
10．函数
的图象是
|
二、填空题：本大题共5小题，每小题5分，共25分，把答案填写在题中的横线上。
11．下列表中的对数值有且仅有一个是错误的：
| x | 3 | 5 | 8 | 9 | 15 |
| lgx | 2a-b | a+c | 3-3a-3c | 4a-2b | 3a-b+c+1 |
请将错误的一个改正为lg =
12． 已知
为锐角，
则
=
=
13．函数
的定义域为
14．已知函数
的反函数是
，则
；
．
15．函数y＝sin(2x＋
)的最小正周期是__________.
三、解答题：本大题共6个小题，共75分。解答应写出文字说明、证明过程或演算步骤。
16. (本小题满分15分)
已知
是R上的奇函数。
（1）求的值；
（2）求的反函数
17（本小题满分15分） 设函数f ( x ) = 2cosx (cosx + 
sinx) – 1 , x ÎR
(1) 求f ( x ) 最小正周期T ;
(2) 求 f ( x ) 单调递增区间；
18. （本小题满分15分）已知中，
．
（Ⅰ）求角
的大小；
（Ⅱ）若
，求周长的取值范围．
19. （本小题满分15分）数列
的前项和为，
，
（Ⅰ）求数列的通项；
（Ⅱ）求数列
的前项和
20. （本小题满分15分）设锐角三角形
的内角
的对边分别为
，
．
（Ⅰ）求
的大小；
（Ⅱ）求
的取值范围．