高三数学月考试题（理科）
一、 选择题 （每小题5分，共50分）
１、已知
A、充分不必要条件 B、必要不充分条件
C、充要条件 D、既不充分也不必要条件
２、设函数
的值为
A、
B、
C、
D、
３、函数
的单调递增区间为
A、
B、
C、
D、
４、如果数列
满足
，则此数列的第
10项为
５、设
函数F（ｘ）的单调递增区间，将F(X)的图像按
平移得一新的函数G(X)的图像，则G(X)的单调递减区间必定是
A、
B、
C、
D、
６、已知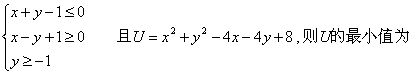
７、
８、
９、若
１０、已知函数
是定义在R上的奇函数，函数
的图象与函数
的图象关于
对称，则
的值为
A、２ B、０ C、１ D、不能确定
一、选择题 （每小题5分，共50分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
|
|
|
|
|
|
|
|
|
|
二、填空题（每小题４分，共２０分）
１１、函数
的图象与直线
有且仅有两个不同的交点，则
的范围是______________。
１２、在△ABC中，S表示△ABC的面积，已知S＝
则tan(B+C)=______。
１３、函数
与函数
的图象关于直线__________________对称。
１４、设
是从－１，０，１这三个整数中取值的数列，若
中有０的个数为_________________。
１５、已知△ABC中，A( 0 , 1 ) , B( 2 , 4 ) ,C( 6, 1 ) , P为平面上任一点，点M，N分别使
给出下列相关命题：① 
②直线MN的方程为
③直线MN必过△ABC的外心 ④向量
所在射线必过N点，上述四个选项中正确的是___________________(将正确的选项全填上)
三、解答题（共８０分）
１６、已知 
求
之值。
１７、解关于ｘ的不等式 
１８、已知数列
中，
且
为负常数，
（１）、用
表示
（２）、
。
１９、已知函数 
（Ⅰ）解关于
的不等式
（Ⅱ）当
时，求
的单调区间。
２０、设年利率为１，将一年平均分割成ｎ个时段（ｎ为正整数），假设每个时段的利率为
，现将１元本金存入银行，我们将按照复利计算（即每一个时段的利息在下一个时段仍然生息），一年后所得到的本金与利息之和记为
（１）、求的表达式
（２）、求证：对于任意的正整数ｎ，有 
２１、设平面上的动向量
为不同时为０的两个实数，实数≥０，满足
，
(Ⅰ)求函数关系式
(Ⅱ)若函数
上单调递增，求的范围；
(Ⅲ)对上述
，当
时，存在正项数列满足
其中
，证明： 
欢迎访问 http://www.k12zy.com