高 三 数 学 试 题(理科)
武汉市新洲区一中 卢有勇 2007.04.25.
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.全卷满分150分,考试时间120分钟.
参考公式:
1.如果事件![]() 、
、![]() 互斥,那么
互斥,那么![]() .
.
2.如果事件![]() 、
、![]() 相互独立,那么
相互独立,那么![]() .
.
3.如果事件![]() 在一次试验中发生的概率是
在一次试验中发生的概率是![]() ,那么
,那么![]() 次独立重复试验中恰好发生
次独立重复试验中恰好发生![]() 次的概率
次的概率![]() .
.
4.球的表面积公式![]() ,其中
,其中![]() 表示球的半径.
表示球的半径.
5.球的体积公式![]() ,其中
,其中![]() 表示球的半径.
表示球的半径.
第Ⅰ卷(选择题 共50分)
一、选择题:本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中, 只有一项是符合题目要求的.
1. 集合![]() , 集合
, 集合![]() ,则
,则
![]() ( )
( )
A. ![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
2. 已知![]() ,其中
,其中![]() 、
、![]() 是实数,
是实数,![]() 是虚数单位, 则
是虚数单位, 则![]() = ( )
= ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3. 函数![]() 是
是![]() 上周期为
上周期为![]() 的奇函数,若
的奇函数,若![]() ,
,![]() , 则( )
A.
, 则( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4. 已知函数![]() 在
在![]() 处取极值10, 则
处取极值10, 则![]() ( )
( )
A. ![]() B.
B. ![]() C.
C.
![]() 或
或![]() D.
D. ![]() 或
或![]()
5. 设![]() 为两两不重合的平面,
为两两不重合的平面,![]() 为两条不重合的直线,给出下列四个命题:
为两条不重合的直线,给出下列四个命题:
①若![]() ∥
∥![]() ,则
,则![]() ;
②若
;
②若![]() ∥
∥![]() ∥
∥![]() ,则
,则![]() ∥
∥![]() ;
;
③若![]()
![]() ④若
④若![]() ⊥
⊥![]() ,则
,则![]() ∥
∥![]() .
.
其中真命题的个数是 ( )
A.1 B.2 C.3 D.4
6. 以椭圆![]() 的长轴的两个端点为焦点,准线过椭圆焦点的双曲线的渐近线 的斜率为 ( )
的长轴的两个端点为焦点,准线过椭圆焦点的双曲线的渐近线 的斜率为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7. 把函数![]() (其中
(其中![]() 是锐角)的图象按
是锐角)的图象按![]() 平移或按
平移或按![]() 平移都可以使对应的新函数成为奇函数,则
平移都可以使对应的新函数成为奇函数,则![]() 的值可为 ( )
的值可为 ( )
A.1 B.2 C.3 D.4
8. ![]() 、
、![]() 为实数且
为实数且![]() ,若多项式函数
,若多项式函数![]() 在区间
在区间![]() 上的导函数
上的导函数![]() 满足
满足![]() ,则以下式子中一定成立的关系式是 ( )
,则以下式子中一定成立的关系式是 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
9. 已知函数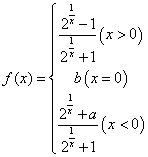 在点
在点![]() 处连续, 则
处连续, 则![]() ( )
( )
A. 2 B. 1 C. 0 D. 3
10. 设F1、F2分别为双曲线![]() 的左、右焦点,
的左、右焦点,![]() 为双曲线右支上任一点,若
为双曲线右支上任一点,若![]() 的最小值为
的最小值为![]() ,则该双曲线离心率
,则该双曲线离心率![]() 的取值范围是 ( )
的取值范围是 ( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
第Ⅱ卷(非选择题 共100分)
二、填空题:本大题共5小题,每小题5分,共25分,把答案填写在答题卡的相应 位置.
11. 设常数![]() ,
,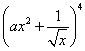 展开式中
展开式中![]() 的系数为
的系数为![]() ,则
,则 ![]() ____
.
____
.
12. 已知变量![]() 、
、![]() 满足
满足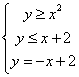 , 则
, 则![]() 的取值范围是
.
的取值范围是
.
13. 已知某篮球选手投篮的命中率为![]() ,且各次投篮间是相互独立的,令此选手投篮
,且各次投篮间是相互独立的,令此选手投篮![]() 次的命中率为
次的命中率为![]() (
(![]() 为进球个数与
为进球个数与![]() 之比),则事件“
之比),则事件“![]() ”发生的概率为
.
”发生的概率为
.
14. 过点![]() 作曲线
作曲线![]() 的切线,则切线方程为
.
的切线,则切线方程为
.
15. 正整数数列按下表排列:
1 2 5 10 17 …
4 3 6 11 18 …
9 8 7 12 19 …
16 15 14 13 20 …
25 24 23 22 21 …
… … … … … …
位于对角线位置的正整数1,3,7,13,21 …构成数列![]() ,则
,则![]() ,
,
通项公式![]() .
.
三、解答题:本大题共6小题,共75分,解答应写出文字说明、证明过程或演算步骤.
16.(本大题满分12分)函数![]()
![]() ,
,
且当![]() 时取函数最小值
时取函数最小值![]() .
.
(I)求![]() 和
和![]() 的值;
的值;
(II) 若![]() 为锐角,且
为锐角,且![]() ,求
,求![]() 的值.
的值.
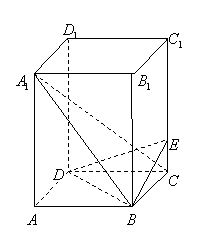 17.(本大题满分12分)如图正四棱柱
17.(本大题满分12分)如图正四棱柱![]() 中,底面边长
中,底面边长![]() ,侧棱
,侧棱![]() ,
,![]() 为线段
为线段![]() 上一点,且
上一点,且![]() .
.
(I)求线段![]() 的长;
的长;
(II)求二面角![]() 的大小.
的大小.
18.(本大题满分12分)某次有奖竞猜活动中有![]() 、
、![]() 两组相互独立的问题,答对问题
两组相互独立的问题,答对问题![]() 可赢得奖金3千元,答对
可赢得奖金3千元,答对![]() 可赢得奖金6千元,规定答题顺序可任选,但只有在一个问题答对后才能解答下一个问题,否则中止答题,已知甲同学答对问题
可赢得奖金6千元,规定答题顺序可任选,但只有在一个问题答对后才能解答下一个问题,否则中止答题,已知甲同学答对问题![]() 、
、![]() 的概率分别为
的概率分别为![]() 和
和![]() .
.
(I)若按先![]() 后
后![]() 的顺序答题,求甲同学获得奖金数
的顺序答题,求甲同学获得奖金数![]() 的分布列和数学期望
的分布列和数学期望![]() ;
;
(II)该甲同学获奖金的期望值的大小与答题顺序有关吗?试证明你的结论.
19.(本大题满分12分)![]() 在以
在以![]() 、
、![]() 为焦点的双曲线
为焦点的双曲线![]() 上的一点,已知
上的一点,已知![]() ,且
,且![]() .
.
(I) 求双曲线的离心率;
(II)过点![]() 作直线分别交双曲线的两渐进线于
作直线分别交双曲线的两渐进线于![]() 、
、![]() 两点,若
两点,若![]() ,
,![]() ,求双曲线的方程.
,求双曲线的方程.
20.(本大题满分13分)已知![]() (
(![]() 为常数),
为常数),
(I)当![]() 时,求
时,求![]() 的单调区间;
的单调区间;
(II)设![]() ,是否存在实数
,是否存在实数![]() 使得
使得![]() 在区间
在区间![]() 上为单调函数,如果存在,求出
上为单调函数,如果存在,求出![]() 的取值范围;若不存在,试说明理由.
的取值范围;若不存在,试说明理由.
21.(本大题满分14分) 集合![]() 是满足下列两个条件的无穷数列
是满足下列两个条件的无穷数列![]() 的集合:
的集合:
① ![]() , ②
, ② ![]() 是与
是与![]() 无关的常数.
无关的常数.
(I) 若![]() 是等差数列,
是等差数列,![]() 是其前
是其前![]() 项和,且
项和,且![]() ,求证:
,求证:![]() ;
;
(II) 设数列![]() 的通项公式为
的通项公式为![]() ,且
,且![]() ,求
,求![]() 的取值范围;
的取值范围;
(III) 设数列![]() 的各项均为正整数,且
的各项均为正整数,且![]() ,求证:
,求证:![]() .
.
参考答案
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | B | C | C | A | B | A | B | B | A | B |
1.B. 集合![]() 是直线
是直线![]() 上的点对应的向量,
上的点对应的向量,![]() 是直线
是直线![]() 上的点对应的向量,它们的交点对应的向量为
上的点对应的向量,它们的交点对应的向量为![]() .
.
2.C. ![]() ,则
,则![]() .
.
3.C.![]() 故
故![]() 或
或![]() .
.
4.A. ![]() 且
且![]() ,得
,得![]() (舍);
(舍);![]() .
.
5.B.①②正确.
6.A.![]() ,渐近线为
,渐近线为![]() .
.
7.B.按![]() 移得
移得![]() 为奇函数,则
为奇函数,则![]() ;
;
按![]() 移得
移得![]() 为奇函数,则
为奇函数,则![]() ,则
,则![]() ,即
,即![]() ,又
,又![]() 为锐角,则
为锐角,则![]() .
.
8.B.可知![]() 在
在![]() 上为减函数,而
上为减函数,而![]() ,故
,故![]() .
.
9.A.![]()
![]() ,
, ![]() ,由
,由![]()
在点![]() 处连续得
处连续得![]() 得
得![]() .
.
10.B.设![]() ,则
,则![]() ,则
,则![]() ,
,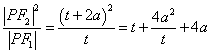
![]() ,当且仅当
,当且仅当![]() 时取等号,
时取等号,![]() .
.
11. 1. 展开式中第![]() 项为
项为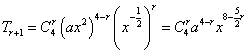 ,
,![]() ,
,![]() ,
,![]() .
.
12.![]() . 由不等式组可得
. 由不等式组可得![]() ,
,![]()
![]()
![]() ,则
,则![]() .
.
13.![]() . 由事件“
. 由事件“![]() ”得投篮4次恰好投中2次,
”得投篮4次恰好投中2次,![]() .
.
14.![]() . 设切点为
. 设切点为![]() ,则
,则![]() ,
,
![]() 切线方程为
切线方程为![]() ,又过点
,又过点![]() ,
,![]() ,
,
![]() ,则
,则![]() 或
或![]() ,即可得切线方程.
,即可得切线方程.
15. 43 ; ![]() . 由题意知
. 由题意知![]() ,由迭代易得通项公式.
,由迭代易得通项公式.
16. 解(I)![]() ,
,
![]() ,
,
其中![]() ,
,
![]() 时
时![]() 取最小值,
取最小值,
当![]() 时,
时,![]()
![]() , 即
, 即![]() ,
,
![]() ,
,
又![]() ,
,![]() .
.
(II)![]() ,
, ![]() ,
,
![]() ,又
,又![]() ,
,
![]() ,
,![]() , 即
, 即![]() .
.
17. 法一(I)![]() 为正四棱柱,
为正四棱柱, ![]() 面
面![]() , 又
, 又![]() 面
面![]() ,
,
![]() ,
,![]() ,
, ![]() ,
, ![]() .
.
(II)由图知二面角![]() 为二面角
为二面角![]() 的余角,
的余角,
设![]() 交于点
交于点![]() ,则
,则![]() ,
,
又![]() 面
面![]() ,
,![]() ,
,![]() 为二面角
为二面角![]() 的平面角,
的平面角,
又![]() ,
,![]() ,
, ![]() ,
,
![]() 的余角为
的余角为![]() ,
,![]() 二面角
二面角![]() 为
为![]() .
.
法二(I)如图建立空间直角坐标系,则![]() ,
,
设![]() ,
,![]() 面
面![]() ,
,![]()
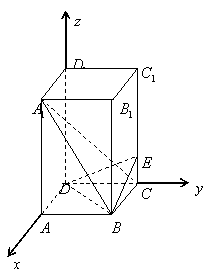 又
又![]() ,
,![]() ,则
,则![]()
![]()
![]() 即
即![]() .
.
(II)面![]() 的法向量为
的法向量为![]() ,
,
面![]() 的法向量为
的法向量为![]() ,
,
![]() ,
,
![]() 二面角
二面角![]() 为
为![]() .
.
18. 解:(I)按先![]() 后
后![]() 的顺序答题获得的奖金数
的顺序答题获得的奖金数![]() 的取值为0,3,9千元,
的取值为0,3,9千元,
![]() ,
,
![]() 的分布列为:
的分布列为:
|
| 0 | 3 | 9 |
|
|
|
|
|
![]() .
.
(II)按先![]() 后
后![]() 的顺序答题获得的奖金数
的顺序答题获得的奖金数![]() 的取值为0,6,9千元,
的取值为0,6,9千元,
![]() ,
,
![]() ,
,
![]() ,故该同学获奖金的期望值与答题顺序无关.
,故该同学获奖金的期望值与答题顺序无关.
19. 解:(I)![]() ,又
,又![]() ,
,![]() , 又
, 又![]() ,
,![]() ,则
,则![]() ,
,
![]() .
.
(II)![]() ,
,![]() ,
,![]() ,
,
故可设双曲线的方程为![]() ,
,![]() 双曲线的渐近线为
双曲线的渐近线为![]() ,
,
![]() ,设
,设![]() ,则
,则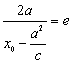 , 则
, 则![]() ,
,
依对称性不妨设点![]() ,
,
由![]() 得
得![]() ①
①
又![]() ,
,![]() ,
,
![]() ,
, 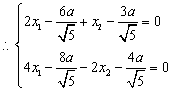 ,
,
则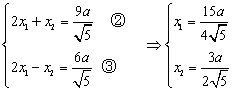 代入①中
代入①中
得![]() ,
,![]() 双曲线为:
双曲线为:![]() .
.
20. (I)![]() ,其定义域为
,其定义域为![]() ,
,
![]() ,
,
当![]() 时,有
时,有![]() ;
; ![]() ,有
,有![]() ,
,
![]() 的增区间为
的增区间为![]() ,减区间为
,减区间为![]() .
.
(II)![]() ,
,
![]() ,
,
若存在实数![]() 使得
使得![]() 在
在![]() 上为单调函数,
上为单调函数,
则![]() 或
或![]() 对于
对于![]() 恒成立,
恒成立,
即![]() 或
或![]() 对于
对于![]() 恒成立,
恒成立,
则![]() 或
或![]() 对于
对于![]() 恒成立,
恒成立,
即![]() 或
或![]() 对于
对于![]() 恒成立,
恒成立,
记![]() ,
,
则![]() ,
,
当![]() 时,
时,![]() ;
; ![]() 时,
时,![]() ,
,
![]() 在
在![]() 上为减函数,在
上为减函数,在![]() 上为增函数,
上为增函数,![]()
又![]() ,
, ![]() ,
,
故![]() 或
或![]() ,
,
即存在![]() 或
或![]() 使
使![]() 在
在![]() 上为单调函数.
上为单调函数.
21. 解(I)设公差为![]() ,则
,则![]() ,
, ![]() ,
,
![]() ,
,
由![]()
![]() , 则
, 则![]() ,满足条件①,
,满足条件①,
又![]() ,
,
当![]() 或
或![]() 时,
时,![]() 取最大值
取最大值![]() ,即
,即![]() ,满足条件②,
,满足条件②,
![]() .
.
(II)![]() ,
,
当![]() 时,
时,![]() ,
,![]() 在
在![]() ,
,![]() 上单调递减,
上单调递减,
当![]() 时,
时,![]() ,即
,即![]()
![]() ,
,![]() .
.
(III)假设存在正整数![]() ,使
,使![]() 成立,
成立,![]() 各项均为正整数,
各项均为正整数,
![]() ,即
,即![]() ,
,
![]() ,
,![]() ,
,
由![]() 及
及![]() 得,
得,![]() ,
,
故![]() ,
, ![]() ,
,
![]() ,
,
……
依此类推有:![]() ,
,
设![]() ,当
,当![]() 时有
时有![]() ,
,
显然与数列![]() 的各项均为正整数矛盾.
的各项均为正整数矛盾.
所以假设不成立,故对于任意![]() ,有
,有![]() 成立.
成立.