高三数学（文）热身考试卷

厦门双十中学2007届高三数学（文）热身考试卷

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　  2007.05.31

1. 设全集是实数集R，M= 等于　

A.{xx<-2}　　 B.{x-2<x<1}　  C.{xx<1或x>2}　  D.{x-2≤x<1}

2.在函数的反函数图象上的一个点可以是　　　　　 　　　　　　　 

（A）　　 （B）　　　　（C）　　　　 （D）

3、在三角形ABC中，“A<60⁰”是“sinA<”的　　　　　　　　　　　　　　　

A．充分不必要条件　　  　　　　B．必要不充分条件

C．充要条件　　　　　　　　　  D．既不充分也不必要条件

4.已知圆被直线所截得的弦长为，则实数的值为　

　 A　0和4　　　  B　1 或3　　　  C　—2或6　　　 D　—1或3

5.已知m，n表示两条不同的直线，α表示一个平面，给出下列四个命题：

　 ①∥n　②∥ ③　④

　　其中正确命题的序号是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

　　　 A．①②　　　　　　　　　 B．②④　　　　　　　　　 C．①④　　　　　　　　　 D．②③

6．已知{a_n}是正项的等差数列，如果满足

则数列{a_n}的前11项的和为

　　　 A．8　　　　　　　　 B．44　　　　　　　　　　 C．56　　　　　　　　 D．64

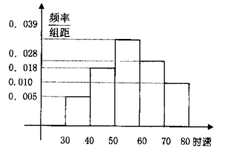
7．200辆汽车经过某一雷达地区，时速频率分布直方图如图所示，

则时速超过70km/h的汽车数量为　　　　　　　　　

　　　 A．1辆　　　　　　 B．10辆　 C．20辆　 D．70辆

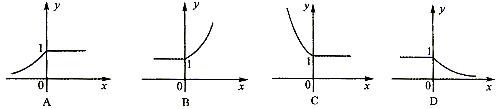
8.定义运算a×b=，则函数的图象大致为　　　　　　　　　　

9．若A，B，C，D，E，F六个元素排成一行，要求A不排在左端，且B，C相邻，则不同的排法有　

A．96种　　　　　　　　　B．120种　　　　　　　　 C．144种　　  D.192

10. 已知抛物线的焦点弦的两端点为,,则关系式

　 的值一定等于 :　　　　　　　　　　　　　　　　　　　 

 A．4　　　 B．－4　　　　　　　 C．1　 　　　　　　　 D．－1　　　

11．函数和，在区间[0，1]上，函数单调递增，则有　　　　　　　　　　　　　　　

  A　　 B　　　　C　　　D　

12．已知函数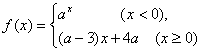满足对任意成立，则a的取值范围是　 　　　　　　　　　　　　　　　　

　　　 A．　　　　　　　　B．（0，1）　　　　　　　C．　　　　　　　　 D．（0，3）

二、填空题

13，已知x、y满足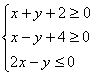则z=2x+y的最大值为　　　 .

14. 已知，设

则=　　　　　

15．　甲、乙两人玩猜数字游戏，先由甲心中想一个数字，记为，再由乙猜甲刚才所想的数字，把乙猜的数字记为，若，就称甲乙“心有灵犀”．现任意找两人玩这个游戏，得出他们“心有灵犀”的概率为　　　　　　　

16. P是椭圆上任意一点，F₁、F₂是它的两焦点，O为坐标原点，，则动点Q的轨迹方程是　　　　  .

三、解答题

17 、（本小题12分）在△ABC中，a,b,c分别为角A，B，C的对边，且4cos2A=

（1）求角A的度数

（2）若a=,b+c=3,求b和c的值

18.某商场准备在节日期间举行促销活动，根据市场调查，该商场决定从3种服装商品、2种家电商品、4种日用商品中，选出3种商品进行促销活动。

　 （1）试求选出的3种商品中至少有一种日用商品的概率；

　 （2）商场对选出的商品采用有奖促销，即在该商品现价的基础上价格提高180元，同时允许顾客每购买1件促销商品有3次抽奖的机会，若中奖，则每次中奖都可获得奖金100元，假设顾客每次抽奖时中奖与否是等可能的，求顾客每购买1件促销商品获奖金不大于100元的概率。

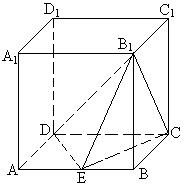
19. (本小题满分12分)

如图, 在正方体—中, 为的中点.

(1) 求和所成的角

(2) 证明: 平面平面;

(3)设

20.  (本小题满分12分)

已知数列{}是首项且公比的等比数列，是其前项的和，成等差数列.

(1) 求和 ;

(2) 证明 12成等比数列.

21. （本小题满分12分）已知椭圆是椭圆上纵坐标不为零的两点，若其中F为椭圆的左焦点.

　 （Ⅰ）求椭圆的方程；

　 （Ⅱ）求线段AB的垂直平分线在y轴上的截距n，并求n的取值范围.

22．（本小题满分14分）已知函数,其图象在横坐标为的两点处的切线均与x轴平行，

（1）求函数的解析式；

　 （2）对于区间[－1，1]上任意两个自变量的值，都有，

试求k的最小值；

　 （3）若过点A（1，m）（m≠－2）可且仅可作曲线y=的一条切线，求实数m的取值范围。

厦门双十中学2007届高三数学（文）热身考试卷参考答案

一、CCADC　BCAD B　　A A

二、13. 16　； 14.　1  ； 15. ；　16.

7．C.　(80-70)×0.01×200=20.

8.解：，选A

9.解：先将AB捆绑当成一个元素，则N=

12解：因，所以f(x)在R上单调递减函数，得0<a<1且a-3<0且

所以解得：

三17、（1）由已知得2[1-cos(B+C)]-(2cos²A-1)=………………(2分)

∵cos(B+C)=-cosA　 ∴4cos²A-4cosA+1=0…………………(4分) 

∴2（cosA-1）²=0即cosA=　 ∴A=60°………………（6分）

（2）∵a²=b²+c²-2bccosA=b²+c²-bc=(b+c)²-3bc

∵a=　b+c=3 ……………………………………………（8分）

∴3=9-3bc　  ∴bc=2…………………………………………（10分）

解得

18.解：（1）从3种服装商品、2种家电商品、4种日用商品中，选出3种商品，一共有

种不同的选法，选出的3种商品中，没有日用商品的选法有种，所以选出的3种商品中至少有一种日用商品的概率为  ……（6分）

（2）顾客在三次抽奖中所获得的奖金总额为ξ（单元：元）

ξ=0表示顾客在三次抽奖中都没有获奖，所以，…………8分

同理可得 ……………………………………10分

　　　　

　　　　　 答：顾客每购买1件促销商品获奖金不大于100元的概率为。…………12分

19．（本小题满分12分）

解: (1) 正方体中, , 与所成的角为或其补角.

, 和所成的角为……………4分

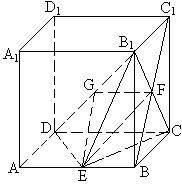
(2) 取的中点的中点连结

平面, .

又, 平面.……………6分

,

四边形是平行四边形,

平面……………7分

又平面, 平面平面……………8分

（2）（法二）建系法，

分别以DC，DD为x,y,z轴建立空间直角坐标。设正方体边长为1，

可求得面

平面平面;

 (3)

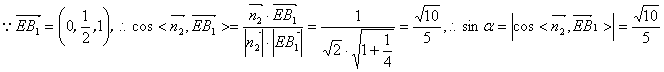
…………12分

20. (本小题满分12分)

由成等差数列，　得，即 　--- 2分

变形得　 所以（舍去）.　　　 --- 4分

(1) ;

　　　　　　　　　　　　　　　　　　　　　　　　　 　　　　 --- 4分

(2) 由 

,

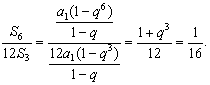
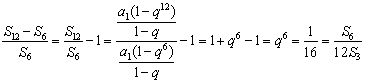所以12成等比数列.　　　　　　　　　　　　　　　　 --- 4分

　　（法二）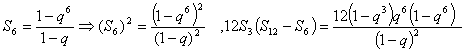

　　　　　 所以，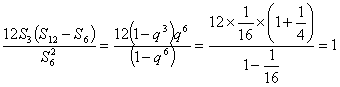

　　　　  所以：12成等比数列.

21．解：

　 （Ⅰ）由已知，得

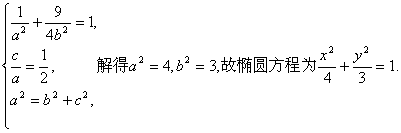………4分

　 （Ⅱ）∵A、B是椭圆上纵坐标不为零的点，

∴A、F、B三点共线，且直线AB的斜率存在且不为0.

又F（－1，0），则可记AB方程为并整理得

……………………………………6分

显然△>0，设

……………………8分

直线AB的垂直平分线方程为

令x=0，得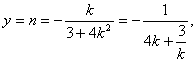……………………………………10分

∵“=”号，

∴，

所以所求的取值范围是……………………………………12分

22．解：（1），依题意，……2分

即 …………4分

（2）∵

当 上为减函数，

　…………6分

∵对于区间[－1，1]上任意两个自变量的值

都有

　 即　

　　　　　　　 …………8分

（3）

∵曲线方程为，∴点A（1，m）不在曲线上。

设切点为M（），则点M的坐标满足

因，故切线的斜率为

整理得（**注：也可以先写出切线方程，然后将点A的坐标代入得到左式）

∵过点A（1，m）仅可作曲线的一条切线，…………………………10分

∴关于x₀方程有且仅有一个实根，

设，则，

从

∴函数 在区间，

的极大、极小值点分别为 …………12分

关于x₀方程有且仅有一个实根的充要条件是：

故所求的实数a的取值范围是{m} …………14分