厦门双十中学2007届高三数学(理)高考热身卷试卷
 一、选择题(本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项符合题目要求)
一、选择题(本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项符合题目要求)
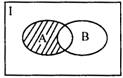
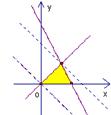
1.如图,阴影部分所表示的集合是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.设复数![]() 为纯虚数,则x= ( )
为纯虚数,则x= ( )
A.-2 B.-1 C.1 D.2
3. 已知x,y满足约束条件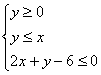 ,则目标函数
,则目标函数![]() 的最大值为 ( )
的最大值为 ( )
A.0 B.3 C.4 D.6
4.已知m,n表示两条直线,α表示一个平面,给出下列四个命题:
①![]() ∥n ②
∥n ②![]() ∥
∥![]() ③
③![]() ④
④![]()
其中正确命题的序号是 ( )
A.①② B.②④ C.①④ D.②③
5.已知{an}是正项的等差数列,如果满足![]() 则数列{an}的前11项的和为( )
则数列{an}的前11项的和为( )
A.8 B.44 C.56 D.64
6.设a,b∈R,则“a+b=1”是“4ab≤1”的( )条件
A.充分非必要 B.必要非充分 C.充分条件 D.既不充分也不必要条件
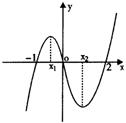 7. 如右图是函数
7. 如右图是函数![]() 的大致图象,则
的大致图象,则![]() =( )
=( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.函数![]() 平移后,得到函数y=g(x),
平移后,得到函数y=g(x),
若y=g(x)是奇函数,则θ可以是( )
A.![]() B.
B. ![]() C.
C.
![]() D.
D.
![]()
9.若A,B,C,D,E,F六个元素排成一行,要求A不排在两端,且B,C相邻,则不同的排法有 ( )
A.72种 B.96种 C.120种 D.144种
10椭圆![]() 与直线
与直线![]() 交于A、B两点,过原点与线段AB中点的直线的斜率为
交于A、B两点,过原点与线段AB中点的直线的斜率为![]() 的值为 ( )
的值为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11.已知函数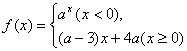 满足对任意
满足对任意![]() 成立,则a的取值范围是 ( )
成立,则a的取值范围是 ( )
A.![]() B.(0,1) C.
B.(0,1) C.![]() D.(0,3)
D.(0,3)
12.定义![]() ,则方程
,则方程![]() =0有唯一解时,实数k的取值范围是( )
=0有唯一解时,实数k的取值范围是( )
A.![]() B.
B.![]() C.
C. ![]() D.
D. ![]()
二、填空题(本大题共4小题,每小题4分,共16分。把答案填在题中的横线上)
13.不等式![]() 的解集是
的解集是
14.在代数式![]() 的展开式中,常数项是
.
的展开式中,常数项是
.
15. 在样本的频率分布直方图中,共有4个小长方形,这4个小长方形的面积由小到大构成等差数列![]() ,已知
,已知![]() ,且样本容量为400,则小长方形面积最大的一组的频数为 ;频率是
,且样本容量为400,则小长方形面积最大的一组的频数为 ;频率是
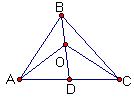
16.已知O是△ABC内一点,![]() ,则△AOB与△AOC的面积的比值为
,则△AOB与△AOC的面积的比值为
三、解答题(本大题共6小题,共74分,解答应写出文字说明,证明过程或演算步骤)
17. (本题满分12分)
在△ABC中,![]() 的对边分别为
的对边分别为![]() 且
且![]() 成等差数列.
成等差数列.
(Ⅰ)求B的值; (Ⅱ)求![]() 的范围。
的范围。
18. (本题满分12分)
某商场准备在节日期间举行促销活动,根据市场调查,该商场决定从3种服装商品、2种家电商品、4种日用商品中,选出3种商品进行促销活动。
(Ⅰ)试求选出的3种商品中至少有一种日用商品的概率;
(Ⅱ)商场对选出的商品采用有奖促销,即在该商品现价的基础上价格提高180元,同时允许顾客每购买1件促销商品有3次抽奖的机会,若中奖,则每次中奖都可获得奖金100元,假设顾客每次抽奖时中奖与否是等可能的,试分析此种有奖促销方案对商场是否有利。
19. (本题满分12分)
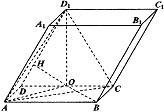
如图,在平行六面体ABCD—A1B1C1D1中,底面ABCD是矩形,AB=2,AD=1,顶点D1在底面ABCD上的射影O是CD的中点,侧棱与底面所成的角为60°。
|
(Ⅱ)求点O到平面AA1D1D的距离;
(Ⅲ)求二面角C—AD1—O的大小。
20. (本题满分12分)
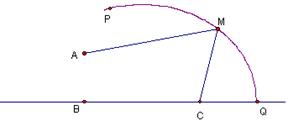
如图,A村在B地正北![]() km处,C村在B地正东4km处,已知弧形公路PQ上任一点到B、C距离之和为8km,
km处,C村在B地正东4km处,已知弧形公路PQ上任一点到B、C距离之和为8km,
(I)建立适当的坐标系,求出公路PQ所在的曲线方程;
(II)现要在公路旁(近似地认为在公路上)建造一个交电房M分别向A村、C村送电,但C村有一村办工厂用电需用专用线路,不得与民用混线用电,因此向C村要架两条线路分别给村民和工厂送电,要使得所用电线长最短,变电房M应建在A村的什么方位,并求出M到A村的距离.
 |
21.(本题满分12分)
已知函数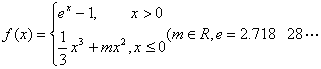 是自然对数的底数).
是自然对数的底数).
(I)求函数![]() 的极值;
的极值;
(II)当x>0时,设![]() 的反函数为
的反函数为![]() 若
若![]() 与
与![]() 的大小.
的大小.
22.(本题满分14分)
已知数列{an}满足a1=5,a2=5,an+1=an+6an-1(n≥2,n∈N*),若数列![]() 是等比数列.
是等比数列.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)求证:当k为奇数时,![]() ;
;
(Ⅲ)求证:![]()
 厦门双十中学2007届高三数学(理)高考热身卷参考答案
厦门双十中学2007届高三数学(理)高考热身卷参考答案
1.B.
2.D.解:![]()
![]() ,依题意得:x=2
,依题意得:x=2
3. C解:如图,过(2,2)点时,Z取最大值=2+2=4
4.C
5.B.解:![]()
![]()
![]()
6.A解:(条件最值)设u=4ab=4a(1-a)=4![]() ,当且仅当a=
,当且仅当a=![]() 时等号成立
时等号成立
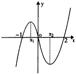 7. A.解:由三根式:
7. A.解:由三根式:![]()
![]() ,依题意,
,依题意,![]() 是
是![]() 的两个根,
的两个根,
8.C解:![]() y=g(x)=
y=g(x)= ![]()
g(x)![]() ,因y=g(x)是奇函数,所以
,因y=g(x)是奇函数,所以![]()
![]() .
.
9.D解:先将AB捆绑当成一个元素,则N=![]()
10.A解: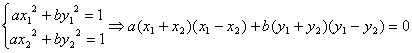
![]()
所以![]() ,所以
,所以![]()
11.A.解:因![]() ,所以f(x)在R上单调递减函数,得0<a<1且a-3<0且
,所以f(x)在R上单调递减函数,得0<a<1且a-3<0且![]() ,所以解得:
,所以解得:![]()
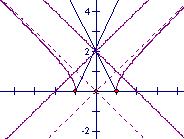 12.A.解:
12.A.解:![]() =0
=0![]()
![]() ,
,
设![]()
方程解的问题转化为两个函数图象的交点
由图可以观察出,![]()
13.解:![]() ---------不用集合表示不得分
---------不用集合表示不得分
14.解:常数项=![]()
15.解:![]() ,所以这4个正方形的面积为
,所以这4个正方形的面积为![]() ,
,
 所以
所以![]()
![]() ,所以面积最的是160. 频率是0.4
,所以面积最的是160. 频率是0.4
16.解1:![]()
![]()
![]()
![]() ,D为
,D为
 AC中点所以设,
AC中点所以设,![]() ,所以
,所以![]()
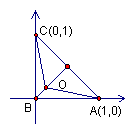
解2:图形特殊化,构造如图所示的等腰直角三角形
则设B(0,0),A(1,0),C(0,1)![]()
![]()
![]()
![]()
![]()
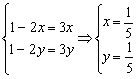
所以△AOB面积=![]() ,△BOC的面积=
,△BOC的面积=![]() ,△ABC的面积=
,△ABC的面积=![]() ,△AOC的面积=
,△AOC的面积=![]() ,所以答案为
,所以答案为![]()
17.(Ⅰ)解法一:![]()
![]() 成等差数列,
成等差数列,
∴ ![]() …………………………………………2分
…………………………………………2分
由正弦定理得,![]()
代入得,![]() 即:sin(A+C)=2sinBcosB
即:sin(A+C)=2sinBcosB
∵A+B+C=π∴sin(A+C)=sinB∴![]() …………………………4分
…………………………4分
又在![]() 中,
中,![]() ,
,![]()
![]() 又
又![]() , ∴
, ∴![]() .……………………6分
.……………………6分
解法二:∵![]() 成等差数列,
成等差数列,
∴![]() …………………………………………2分
…………………………………………2分
由余弦定理,![]()
化简得, ![]() ……………………4分
……………………4分
∴![]() ∵
∵ ![]() ………………………6分
………………………6分
(Ⅱ)解:![]()
![]() ,
,![]()
∴![]() …………………8分
…………………8分
![]()
![]() ……………………………………………………10分
……………………………………………………10分
![]()
![]() ,
,![]()
![]()
![]() 的范围是
的范围是![]() ……………………12分
……………………12分
18.解:(1)从3种服装商品、2种家电商品、4种日用商品中,选出3种商品,一共有
![]() 种不同的选法,选出的3种商品中,没有日用商品的选法有
种不同的选法,选出的3种商品中,没有日用商品的选法有![]() 种,
种,
所以选出的3种商品中至少有一种日用商品的概率为 ![]() ……(4分)
……(4分)
(注:没有描述好P的意义扣1分)
(2)顾客在三次抽奖中所获得的奖金总额是一随机变量ξ,-----------------------------------------5分
其所有可能的取值为0,100,200,300。(元)
所以![]() ,
,
![]()
![]()
![]() -----------每个1分---------9分
-----------每个1分---------9分
于是顾客在三次抽奖中所获得的奖金总额的期望值是
![]() …………11分
…………11分
故促销方案对商场有利。…………12分
19.(Ⅰ)证明:![]()
![]() 在平面
在平面![]() 上的射影为O,
上的射影为O,![]() ,
, ![]()
![]() 点
点![]() 为
为![]() 的中点,
的中点,![]() ,
,![]() OC=1又
OC=1又![]() ,
,![]() ,∠BOC=45°
,∠BOC=45°
同理∠AOD=45°, ∴∠AOB=90°。 ∴![]()
![]() ,
,![]() …………………………4分(没有指出两线相交扣1分)
…………………………4分(没有指出两线相交扣1分)
(Ⅱ)解法一:![]() ,
,![]() 又
又![]()
![]() ,
,![]() AD
AD![]() 平面
平面![]()
![]() 在平面
在平面![]() 内,作
内,作![]() ,垂足为
,垂足为![]() ,
,
则![]() 。
。 ∴线段
∴线段![]() 的长为点
的长为点![]() 到平面
到平面![]() 的距离
的距离
![]()
![]()
![]() 在平面
在平面![]() 上的射影为
上的射影为![]() 。
。
![]()
![]() 为侧棱
为侧棱![]() 与平面
与平面![]() 所成的角.
所成的角.![]()
在![]() 中,
中,![]() =
=![]() 。即点
。即点![]() 到平面
到平面![]() 的距离为
的距离为![]() ……8分
……8分
解法二:∵D1O⊥平面ABCD,∴DD1在平面ABCD上的射影为DO
∴∠D1DO为棱DD1与平面ABCD所成的角, ∴∠D1DO=60°∵OD=1, ∴![]()
∴![]()
∵AD⊥DO,AD⊥D1O, ∴AD⊥平面D1DO ∴AD⊥DD1,设点O到平面ADD1A1的距离为h,
则![]()
 ∵
∵![]() 即点O到平面ADD1A1的距离为
即点O到平面ADD1A1的距离为 ![]() ………10分
………10分
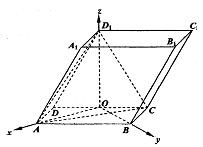
解法三:由(Ⅰ)可得,OA,OB,OD1的两两垂直以点O为坐标原点,分
别以射线OA,OB,OD1所在直线为x轴,y轴,z轴建立空间直角坐标系。
∵D1O⊥平面ABCD,∴DD1在平面ABCD上的射影为DO
∴∠D1DO为棱DD1与平面ABCD所成的角。∴∠D1DO=60°
∵OD=1, ∴![]() ∴
∴![]()
∴![]()
![]() 设平面ADD1的一个法向量为n=(a,b,c),则
设平面ADD1的一个法向量为n=(a,b,c),则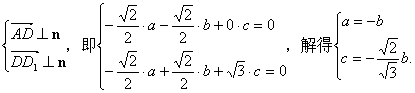
不妨令 ![]() ∴点O到平面ADD1的距离
∴点O到平面ADD1的距离
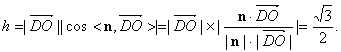 ………………8分
………………8分
(Ⅲ)解:如图,作![]() 于
于![]() ,作
,作![]() 于
于![]() ,连结
,连结![]()
![]() ,
,![]() 又
又![]() ,
,![]()
又![]() ,
,![]()
![]() 为二面角
为二面角![]() 的平面角,
的平面角,
在![]() 中,
中,![]() ,
,![]() ,
,![]() .
.
在![]() 中,
中,![]() ,
,![]() ,
,![]()
取![]() 的中点
的中点![]() ,连结
,连结![]() ,则
,则![]() ,
,![]()
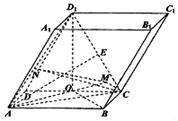
![]()
![]() ,
,![]()
在![]() 中,
中,![]()
![]() .
.
二面角![]() 的大小为
的大小为![]() .………………………………12分
.………………………………12分
20. 解:(1)如图,以BC的中点为原点,BC所在的直线为x轴建立直角坐标系,----------1分
则B(-2,0),C(2,0),A(-2,![]() ),---------------2分
),---------------2分
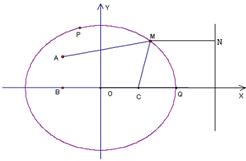 ∵MB+MC=8(8>BC=4),
∵MB+MC=8(8>BC=4),
∴M在以B、C为焦点,长轴长为8的椭圆上.-----------4分
得椭圆方程为![]() .-----------6分
.-----------6分
(2)其离心率为![]() ,右准线为l:x=8.
,右准线为l:x=8.
作MN⊥l,垂足为N,则AM+2MC=AM+MN,-----------8分
可见,当M在AN上时,AM+2MC最小,此时M的纵坐标为![]() ,-----------10分
,-----------10分
∴M的纵坐标为![]() ,故得M在A正东且距A为(2+2
,故得M在A正东且距A为(2+2![]() )km处.-----12分
)km处.-----12分
点评:2004年广东高考数学试题中,就有一道解析几何应用性的问题,它实质是来源于课本,你知道吗?
21.解:(I)∵当x>0时,![]() 上单调递增,且
上单调递增,且![]() ;
;
当x≤0时,![]() ,此时
,此时![]() …………2分
…………2分
①若m=0时,![]() 上单调递增,且
上单调递增,且![]() .
.
又![]() ,可知函数
,可知函数![]() 在R上单调递增,无极值.…………………………3分
在R上单调递增,无极值.…………………………3分
②当m<0,令![]() (舍去)
(舍去)
函数![]() 上单调递增,
上单调递增,
同理,函数![]() 在R上单调递减,无极值, ………………4分
在R上单调递减,无极值, ………………4分
③若![]()
函数![]() 上单调递增,在(-2m,0
上单调递增,在(-2m,0![]() 上单调递减.
上单调递减.
此时函数![]() 在x=-2 m处取得极大值:
在x=-2 m处取得极大值:![]() ;
;
又![]() 在(0,+∞)上单调递增,故在x=0处取得极小值:f(0)=0.
在(0,+∞)上单调递增,故在x=0处取得极小值:f(0)=0.
综上可知,当m>0时,![]() 的极大值为
的极大值为![]() ,极小值为0;当m≤0时,
,极小值为0;当m≤0时,![]() 无极值. …6分
无极值. …6分
(II)当x>0时,设y=f(x)=ex-1![]()
![]() 7分
7分
解1:比较![]() 的大小.
的大小.
记![]() ……………………………………………8分
……………………………………………8分
![]() 上是单调递增函数,(
上是单调递增函数,(![]() )……9分
)……9分
![]() 恒成立. ∴函数
恒成立. ∴函数![]() 上单调递增. ……………10分
上单调递增. ……………10分
![]()
当0<p<q时,有q-p>0,![]()
![]() ……………12分
……………12分
解2:![]() ,设函数
,设函数![]() (x>p)
(x>p)
则![]() 在
在![]() 上是单调递增,(
上是单调递增,(![]() >0)
>0)
![]() 恒成立 ∴函数
恒成立 ∴函数![]() 上单调递增,又在x=p处连续
上单调递增,又在x=p处连续
![]()
所以当q>p时,g(q)>g(p),即![]() 所以
所以![]()
22.解(Ⅰ)∵![]() 为等比数列,
为等比数列,
∴![]()
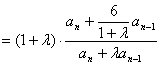 应为常数,
应为常数,
∴![]() 得
得![]() =2或
=2或![]() =-3 ……………………2分
=-3 ……………………2分
当![]() =2时,可得
=2时,可得![]() 为首项是
为首项是 ![]() ,公比为3的等比数列,
,公比为3的等比数列,
则![]() ①………………4分
①………………4分
当![]() =-3时,
=-3时,![]() 为首项是
为首项是![]() ,公比为-2的等比数列,
,公比为-2的等比数列,
∴![]() ②
②
①-②得, ![]() ……………6分(注:也可由①利用待定系数或同除2n+1得通项公式)
……………6分(注:也可由①利用待定系数或同除2n+1得通项公式)
(Ⅱ)当k为奇数时,![]()
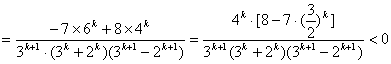 ∴
∴ ![]() …10分
…10分
(Ⅲ)由(Ⅱ)知k为奇数时, ![]() …………12分
…………12分
①当n为偶数时, ![]()
②当n为奇数时,![]()
![]()
=![]() ………………14分
………………14分