高三教学质量检查数学（一）文科

福建省诏安一中2007年高三教学质量检测

　　　　　　　  数 学 试 题（文科）　　　 2007.06.1

考试时间：120分钟 　　满分：150分　　 

一．选择题：每小题5分，共60分．

题　号	1	2	3	4	5	6	7	8	9	10	11	12
答　案	A	B	D	D	B	A	D	B	A	D	B	B

二、填空题：本大题共4小题，每小题4分，共16分

13．６人　　　14．（０，２）　　　 15．1 80　　　16．

三、解答题：本大题共6小题，共74分．解答应写出文字说明、证明过程或演算步骤

17．本小题考查三角函数的定义域、值域以及三角函数式的变换。

解：（1）∵m⊥n，∴m·n＝0，∴cosA＋1－sinA＝0 （2分）

sinA－cosA＝1，sin（A－）＝　（4分）

∵0<A<π，  ∴－<A－<，A－＝，  ∴A＝　（6分）

（2）∵b＋c＝a，∴由正弦定理得：sinB＋sinC＝sinA＝　（8分）

∵B＋C＝，∴sinB＋sin（－B）＝·cosB＋sinB＝ （10分）

即sin（B＋）＝　（12分）

18．解：（1）该同学恰好得3分的概率为P＝＝　（6分）

（2）P（ξ＝6）＝＝＝，P（ξ＝12）＝＝

该同学得分不少于6分的概率为P＝P（ξ＝6）＋P（ξ＝12）＝　（12分）

19．（本小题满分12分）

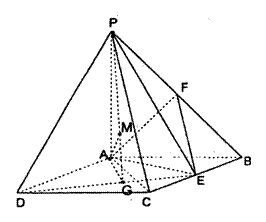　　解：（1）三棱锥E—PAD的体积

……………4分

 （2）当点E为BC的中点时，EF与平面PAC平行.

　　　 ∵在△PBC中，E、F分别为BC、PB的中点，

　　　 ∴EF∥PC，又EF分别为BC、PB的中点，

　　　 ∴EF//PC，又EF平面PAC，而PC平面PAC，

　　　 ∴EF//平面PAC.……………………………………8分

　　  （3）证明：∵PA⊥平面ABCD，BE平面ABCD，

　　　 ∴EB⊥PA，又EB⊥AB，AB∩AP=A，AB，AP平面PAB,

　　　 ∴EB⊥平面PAB，又AF平面PAB，∴AF⊥PB，

　　　 又PA=AB=1，点F是PB中点，

　　　 ∴AF⊥PB又∵PB∩BE=B，

　　　 PB，BE面PBE，

　　　 ∴AF⊥面PBE　∵PE面PBE　∴AF⊥PE　　　　　　………12分

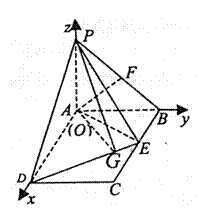解法二：（向量法）（I）（II）同解法一

（Ⅲ）建立图示空间直角坐标系，

则P（0，0，1），B（0，1，0），

设

∴AF⊥PE

20．本小题考查等比数列的性质、通项公式，以及对数的运算及二次函数最值的求法.

解：（1）设数列{a_n}的公比为q.

由等比数列性质可知：，

而　，　　　　　　　　　　　　　　　　（3分）

由（舍），故　　（6分）

　 （2）

　　 ，　　　　　　　　　　　　　　　　（10分）

∴当n = 3时，T_n的最大值为9lg2.　　　　　　　　　　　　　　　　　　　　　　　　　　 （12分）

20．（12分）

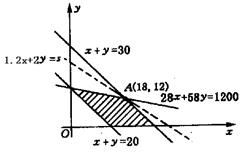
　 解：设初中x个班，高中y 个班，则……………（4分）

　 设年利润为s，则

　 ……（6分）

　 作出（1）、（2）表示的平面区域，如图，易知当直线1.2x+2y=s过点A时，s有最大值.

　 由解得A（18，12）.……（10分）

　 （万元）.

　 即学校可规划初中18个班，高中12个班，

可获最大年利润为45.6万元.……（12分）

21．解：

（1）设C：＋＝1（a>b>0），设c>0，c²＝a²－b²，由条件知－c＝＝，＝，

∴a＝1，b＝c＝，

故C的方程为：y²＋＝1　（6分）

（2）由＝λ得－＝λ（－），（1＋λ）＝＋λ，

∴λ＋1＝4　　λ＝3　（6分）

设l与椭圆C交点为A（x₁，y₁），B（x₂，y₂）

得（k²＋2）x²＋2kmx＋（m²－1）＝0

Δ＝（2km）²－4（k²＋2）（m²－1）＝4（k²－2m²＋2）>0 （*）

x₁＋x₂＝， x₁x₂＝　（10分）

∵＝3 ∴－x₁＝3x₂ ∴

消去x₂，得3（x₁＋x₂）²＋4x₁x₂＝0，∴3（）²＋4＝0

整理得4k²m²＋2m²－k²－2＝0　（12分）

m²＝时，上式不成立；m²≠时，k²＝，

由（*）式得k²>2m²－2

因λ＝3 ∴k≠0 ∴k²＝>0，∴－1<m<－或<m<1

即所求m的取值范围为（－1，－）∪（，1）　（14分）