山东省临沂市2007学年高三教学质量检查考试（二）
数学（文）试题
本试题分为第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。共150分，考试时间120
分钟.
第Ⅰ卷（选择题，共60分）
注意事项：
1．答第I卷明，考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上.
2．每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑. 如需改动，用橡皮
擦干净后，再选涂其它答案，不能答在试卷上.
3．考试结束后，将本试卷和答题卡一并收回.
|
1．设集合I={－2，－1，0，1，2}，A={1，2}，B={－2，－1，2}，则
（ I B）=（ ）
A．{1} B．{1，2} C．{2} D．{0，1，2}
2．复数
的值是 （ ）
A．2i B．－2i C．2 D．－2
3．抛物线
的准线方程是
，则a的值为 （ ）
A．
B．－ C．4 D．－4
|
的图象大致是 （ ）
|
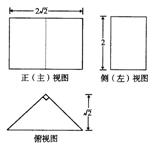
等腰直角三角形（如图），根据图中标注的长度，可以计算出
该几何体的表面积是 （ ）
A．12+4
B．8+4
C．2+8 D．6+4
6．一个容量为20的样本，数据的分组及各组的频数如下表
|
则样本区间
上的频率为（其中
） （ ）
A．0.5 B．0.7 C．0.25 D．0.05
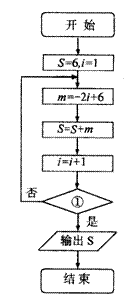7．如果右边程序框图的输出结果为－18，那么在判断框中①表示
的“条件”应该是 （ ）
A．
B．
C．
D．
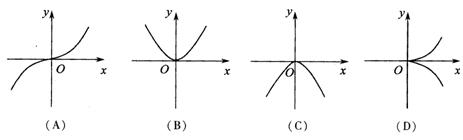
8．已知函数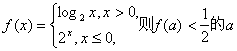
的取值范围是
（ ）
A．
B．
C．
D．
9．若点P是曲线
上任意一点，则点P到直线
的最小距离为
（ ）
A．1 B． C．
D．
|
A．
B．
C． D．
11．已知向量
、
的夹角为60°，则直线
的位置关系是 （ ）
A．相交 B．相交且过圆心 C．相切 D．相离
12．已知函数
的大小关系是
（ ）
A．
B．
C．
D．大小与
有关
|
二、填空题：本大题4小题，每小题4分，共16分. 把答案填写在题中横线上.
13．函数
恒过定点
.
14．为了判断高中三年级学生选修文科是否与性别有关，现随机抽取50名学生，得到如下2 ×2列联表：
| 理科 | 文科 | |
| 男 | 13 | 10 |
| 女 | 7 | 20 |
已知
根据表中数据，得到
.
则认为选修文科与性别有关系出错的可能性为 .
15．已知变量
满足
的最大值为12，则k的值等于
.
16．有下列说法：
①命题
R，
R，
；
②已知直线
；
③兵乓球赛前，决定谁先发球，抽鉴方法是从1—10共10个数中各抽1个，再比较大小，这种抽鉴方法是公平的；
④若函数
R，则
其中正确的序号是 .
三、解答题：本大题共6小题，共74分.
17．（本小题满分12分）
在△ABC中，三个内角A，B，C所对的边长分别为a，b，c. 若向量m=（a，b）
与n=（cosA，cosB）
（I）判断△ABC的形状；
（II）当
取得最大值时，求角A.
18．（本小题满分12分）
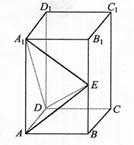
在长方体ABCD—A1B1C1D1中AB=BC=1，AA1=2，E是侧棱BB1的中点.
|
（II）求三棱锥A1—ADE的体积.
19．（本小题满分12分）
设数列
的前n项和为
为等比数列，且
.
（I）求数列，
的通项公式；
（II）设
，求数列{
}的前n项和Tn.
20．（本小题满分12分）
预计某地区明年从年初开始的前x个月内，对某种商品的需求总量
（万件）
近似满足：
N*，且
）
（I）写出明年第x个月的需求量g（x）（万件）与月份x的函数关系式，并求出哪个月份的需求量超过192万件；
（II）如果将该商品每月都投放市场P万件，要保证每月都满足供应，P应至少为多少万件？（不计积压商品）
21．（本小题满分12分）
已知直线
相交于A、B两点，且
（I）求椭圆C的离心率；
（II）若椭圆C的右焦点关于直线l的对称点在圆
上，求椭圆C的方程.
22．（本小题满分14分）
已知
的一个极值点，其中
R，
.
（I）求m与n的关系式；
（II）求的单调区间；
（III）若
，求证：函数的零点有且只有1个.
参考答案
说明：
一、本解答只给出一种解法供参考，如果考生的解法与本解答不同，可根据试题的主要考查内容对照评分标准制订相应的评分细则.
二、对计算题，当考生的解答在某一步出现错误时，如果后继部分的解答未改变该题的内容与难度，可视影响的程度决定后继部分的给分，但不得超过该部分正确解答应得分数的一半；如果后继部分的解答有较严重的错误，就不再给分.
三、解答右端所注分数，表示考生正确做到这一步应得的累加分数.
四、只给整数分数，选择题和填空题不给中间分.
一、选择题：（每小题5分，满分60分）
1． D 2．B 3．B 4．A 5．A 6．B 7．A 8．D 9．B 10．C 11．D 12．C
|
13．（1，0） 14．5% 15．－9 16．③④
三、解答题：（满分74分）
17．解：（I）
m与n共线，
…………2分
由正弦定理，得
…………4分
∵A、B为三角形的内角，
∴A=B， …………5分
∴△ABC为等腰三角形. …………6分
（II）
， …………9分
∵A=B，
∴
…………10分
当且仅当
值最大，即
当y值最大时，
…………12分
18．（I）证明：在长方体ABCD—A1B1C1D1中，棱DA⊥A1B1BA，
∵A1E
面A1B1BA，∴DA⊥A1E …………2分
在长方形ABB1A1中，AB=1，A1A=2，E为BB1中点
∴AE=A1E=，
∴AE2+A1E2=A1A2，
∴A1E⊥AE …………6分
∴A1E⊥面AED. …………12分
（II）
…………12分
19．解：（I）
…………1分
N* …………3分
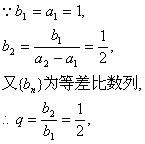
N*） …………6分
（II）
…………7分
①
② …………9分
①—②得
…………12分
20．解：（I）
（万件） …………1分
N*且）. …………3分
由
…………4分
化简得
，
解得
。 …………5分
又x
N*，
=5，6，7.
答：第5，6，7月份的需求量超过192万件. …………6分
（II）保证每月都满足供应，则
N*，恒成立 …………8分
的最大值为216（万件）……10分
…………11分
答：每月至少应投放216万件. …………12分
21．解：（I）设
.
…………1分
由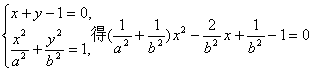
. …………3分
该方程的两根为
，由韦达定理，得
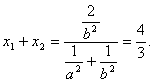…………4分
…………5分
，
…………6分
（II）设椭圆的右焦点为F（c，0），F关于直线l的对称点为
，
则
…………8分
…………10分
…………11分
故所求椭圆方程为
. …………12分
22．（I）
…………2分
的一个极值点，
（II）由（I）知
…………5分
若
为增函数，
当
为减函数，
的减区间. …………7分
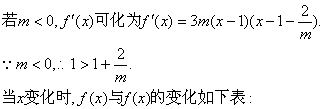
| x |
|
|
| 1 |
|
|
| <0 | 0 | >0 | 0 | <0 |
|
| 单调递减 | 极小值 | 单调递增 | 极大值 | 单调递减 |
故由上表知，当
在
上单调递减，即
增区间是
…………10分
（III）证明：
由（II）知，在
，
上无零点. …………12分
…………13分
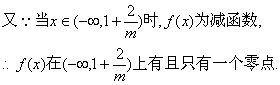
综上可知，的零点有且只有一个. …………14分