山东省临沂市2007学年高三教学质量检查考试（二）
数学试题（理）
本试题分为第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分.共150分，考试时间120分钟.
第Ⅰ卷（选择题，共60分）
注意事项：
1．答第I卷前，考生务必将自己的姓名、准考证号、考试科目涂写在答题卡上。
2．每小题选出答案后，用铅笔把答题卡对应题目的答案标号涂黑。如需改动，用橡皮
擦干净后，再选涂其它答案，不能答在试卷上。
3．考试结束后，将答题卡和第Ⅱ卷一并交回。
一、选择题：本大题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是最符合题目要求的。
1．函数
的最小正周期是 （ ）
A．2 
B． C．2 D．1
2．若集合A、B、C满足A∪B=A∪C，那么下列各式中一定成立的是 （ ）
A．A∩B=A∩C B．B=C
|
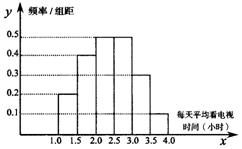
3．为了解电视对生活的影响，就平均每天看
电视的时间，一个社会调查机构对某地居
民调查了10000人，并根据所得数据画出
样本的频率分布直方图（如图），为了分析
该地居民平均每天看电视的时间与年龄、学
历、职业等方面的关系，要从这10000人中
再用分层柚样方法抽出100人做进一步调查，
则在
（小时）时间段内应抽出的人数是（ ）
A．25 B．30 C．50 D．75
|
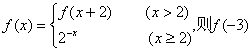的值为 （ ）
A．2 B．8
C．
D．
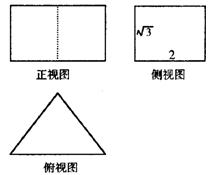
5．有一个正三棱柱，其三视图如图，则其
体积等于 （ ）
A．3 B．1
C．
D．4
6．已知函数
= （ ）
A．1 B．1－cos1 C．0 D．cos1－1
7．等差数列{an}中，Sn是其前n项和，
则S2008的值为（ ）
A．－2006 B．2006 C．－2008 D．2008
8．若点P是曲线y=x2－lnx上任意一点，则点P到直线y=x－2的最小距离为 （ ）
A．1 B．
C．
D．
|
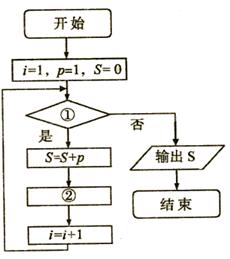
第1个数是1，第2个数比第1个数大1，第3
个数比第2个数大2，第4个数比第3个数大3，
以此类推，要计算这50个数的和.现已给出了该
问题算法的程度框图如图，请在图中判断框中的
①处和执行框中的②处填上合适的语句，使之能
完成该题算法功能（ ）
A．i≤50；p=p+i
B．i<50；p=p+i
C．i≤50；p=p+1
D．i<50；p=p+1
10．如图的阴影部分由方格纸上3个小方格组成，我们
称这样的图案为L形，那么在由3×5个小方格组
成的方格纸上可以画出不同位置的L形图案的个数
|
A．15 B．16 C．32 D．48
|
的焦点F
恰好是椭圆
的左焦点，且两
曲线的公共点的连线过F，则该椭圆的离
心率为 （ ）
A． B．2（－1） C．
D．－1
12．设O为坐标原点，点M（2，1），点N（x，y）满足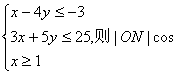
∠MON的最大值为 （ ）
A．
B．
C．
D．
|
注意事项：
1．第Ⅱ卷用钢笔或圆珠笔直接答在试题卷中。
2．答卷前将密封线内项目填写清楚。
二、填空题：本大题共4小题，每小题4分，共16分.把正确答案填在题中横线上.
13．已知双曲线的中心在原点，一个顶点的坐标是（－3，0），且焦距与实轴长之比为5：3，则双曲线的标准方程是 .
|
的展开式的常数项是
.
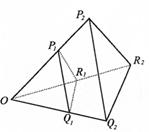
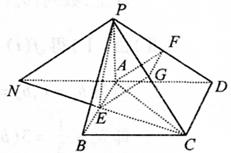
15．若从点O所作的两条射线OM，ON上分别有点M1，
M2与点N1，N2，则三角形面积之比
.
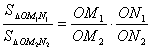如图，若从点O所作的不在同一平面内的三条射线
OP，OQ和OR上分别有有点P1，P2，点Q1，Q2和
点R1，R2，则类似的结论为 .
16．有下列说法：
①函数
的零点所在的大致区间是（2，3）；
|
③一组数据方差越小，样本数据分布越集中、稳定；
④乒乓球赛前，决定谁先发球，抽签方法是从1~10共10个数中各抽1个，再比较大
小，这种抽签方法是公平的；
⑤若函数
的值域是R，则a≤－4或a≥0.
三、解答题：本大题共6小题，共74分，解答应写出文字说明，证明过程或演算步骤
17．（本小题满分12分）
在△ABC中，a、b、c分别是角A、B、C的对边，
，且x⊥y.
（I）求角A的大小；
（II）当
取最大值时，求角B的大小；
18．（本小题满分12分）
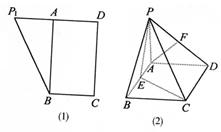
如图（1），在直角梯形P1DCB中，P1D//BC，CD⊥P1D，且P1D=8，BC=4，DC=4
，A是P1D的中点，沿AB把平面P1AB折起到平面PAB的位置（如图（2）），使二面角P—CD—B成45°，设E、F分别是线段AB、PD的中点.
（I）求证：AF//平面PEC；
（II）求平面PEC和平面PAD所成的二面角（锐角）的大小.
|
19．（本小题满分12分）
数列
=
（I）求证：数列{an}是等比数列；
（II）设数列{an}的公比为f(t)，作数列{bn}，使
，求数列{bn}的前n项和Bn.
20．（本小题满分12分）
在一个盒子里放有6张卡片，上面标有数字1，2，3，4，5，6，现在从盒子里每次任意取出一张卡片，取两片.
（I）若每次取出后不再放回，求取到的两张卡片上数字之积大于12的概率；
（II）在每次取出后再放回和每次取出后不再放回这两种取法中，得到的两张卡片上的最大数字的期望值是否相等？请说明理由.
21．（本小题满分12分）
已知
，直线l：y=－2，动点P到直线l的距离为d，且d=
.
（I）求动点P的轨迹方程；
（II）直线m:y=
与点P的轨迹交于M、N两点，当
时，求直线m的倾斜角α的取值范围；
（III）设直线h与点P的轨迹交于C、D两点，写出命题“如果直线h过点B，那么
=－12”的逆命题，并判断该逆命题的真假，请说明理由.
22．（本小题满分12分）
某化工企业生产某种化工原料，在生产过程中对周边环境将造成一定程度的污染，过去没有采取任何治理污染的措施，依据生产和营销的统计数据发现，该企业每季度的最大生产能力为2万吨，且每生产x万吨化工原料，获得的纯利润y（百万元）近似地满足：y=(x+1)ln(x+1).自2007年3月人民代表大会召开后，该企业认识到保护环境的重要性，决定投入资金进行的污染治理，计划用于治理污染的资金总费用为y1=2px（百万元）（其中x为该工厂的生产量，p为环保指标参数，p∈
.
（I）试写出该企业进行污染治理后的利润函数
；
（II）试问p控制在什么范围内，该企业开始进行污染治理的第一个季度，在最大生产能力的范围内始终不会出现亏损？
参考答案
说明：
一、本解答只给出了一种解法供参考，如果考生的解法与本解答不同，可根据试题的主要考查内容对照评分标准制订相应的评分细则。
二、对计算题，当考生的解答在某一步出现错误时，如果后继部分的解答未改变该题的内容与难度，可视影响的程度决定后继部分的给分，但不超过该部分正确解答应得分数的一半；如果后继部分的解答有较严重的错误，就不再给分.
三、解答右端所注分数，表示考生正确做到这一步应得的累加分数。
四、只给整数分数，选择题和填空题不给中间分。
一、选择题：（每小题5分，满分60分）
1.C 2.D 3.A 4.C 5.D 6.B 7.C 8.B 9.A 10.C 11.D 12.B
|
13.
14.60 15.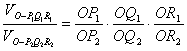 
16. ①③④⑤
三、解答题：（满分74分）
17．（I）解：由x⊥y得 x·y=0，从而（2b－c）cosA－acosC=0，……………………1分
由正弦定理得2sinBcosA－sinCcosA－sinAcosC=0，…………………………2分
∴2sinBcosA－sin(A+C)=0，………………………………………………………3分
∴2sinBcosA－sinB=0，…………………………………………………………4分
∵
……………………6分
（II）
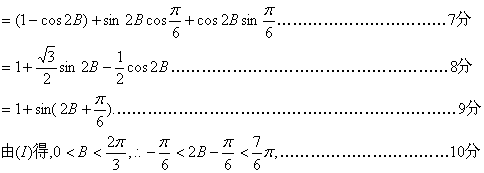
取得最大值.………………………………12分
18．解：（I）如图，设PC中点为G，连结FG，…………………………………1分
则FG//CD//AE，且FG=CD=AE，
∴四边形AEGF是平行四边形.………………………………………………2分
∴AF//EG，又∵AF
平面PEC，EG
平面PEC，
∴AF//平面PEC………………………………………………………………4分
（II）连结AC，在折前BA⊥AD，BA⊥AP1，折后有BA⊥AD，BA⊥AP，
∴BA⊥平面PAD，又CD//AB，∴CD⊥PD,
|
∴∠ADP=45°.……………………6分
又PA=AD=4,∴△PAD为等腰直角三角形，
∴PA⊥AD，∴PA⊥平面ABCD.……………8分
解法一：如图，延长DA，CE交于点N，连结PN.
∵AE//CD且E为AB中点，
∴AE=CD，AE为△NCD的中位线，
∴AN=AD=PA，△PND为直角三角形.
又NE=EC=2
，PE=2，
∴△PNC为直角三角形，
∴PC⊥PN，PD⊥PN，∴∠CPD为平面PEC和平面PAD所成二面角的平面角.
………………………………………………………………10分
又PD=4，CD=4，PD⊥CD，
∴tan
……………………11分
∴∠CPD=60°，即平面PEC和平面PAD所成二面角为60°.…………12分
|
为x轴、y轴、z轴，
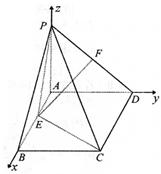
建立空间直角坐标系，则A（0，0，0），
B（4，0，0），C（4，4，0）D（0，4，0），
P（0，0，4），E（2，0，0）.…………6分
∴
是平面PAD的法向量.……8分
设平面PEC的一个法向量为n=（1，y，z），
.
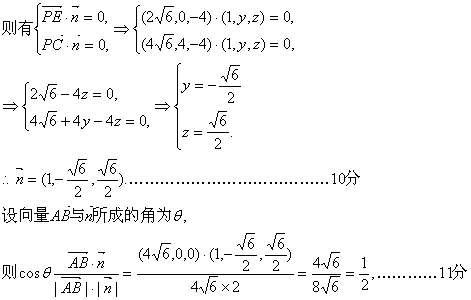
∴向量
所成的角为60°，
故平面PEC和平面PAD所成的二面角（锐角）为60°.……………………12分
19．解：（I）∵3tSn－(2t+3)Sn－1=3t，①
从而有3tSn+1－(2t+3)Sn=3t. ②…………………………1分
②－①得 3t(Sn+1－Sn)－(2t+3)(Sn－Sn－1)=0，
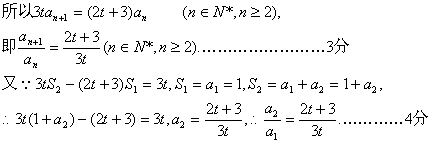
综上，数列{an}是以1为首项，
为公比的等比数列.…………5分
（II）由（I）得，
.……………………………………6分
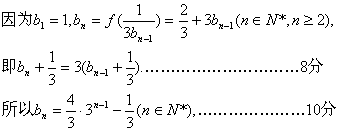
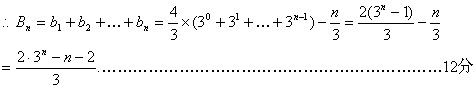
20．解：（I）取到的两张卡片上数字之积大于12的事件为3，4，5，6四个数中取出两个，且应除去3，4两个数字。
故所求事件概率
.…………………………………………4分
（II）若每次取出后不再放回，则得到的两张卡片上的数字中最大数字随机变量ξ，ξ=2，3，4，5，6.
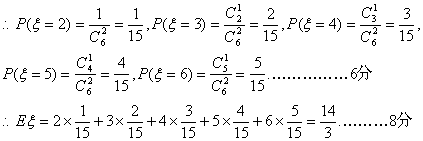
若每次取出后再放回，则得到的两张卡片上的数字中最大数字是随机变量，η，
η=1，2，3，4，5，6.
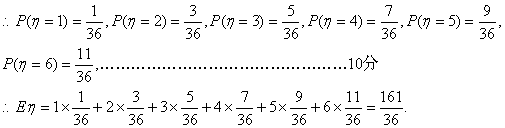∴在每次取出后再放回和每次取出后不再取回这两种取法中，得到的两张卡上的数
字中最大数字的期望值不相等.………………………………………………12分
21．解：（I）由题意知，动点P的直线l的距离与P到定点B的距离相等.
∴P的轨迹是B为焦点，l为准线的抛物线，………………1分
点P的轨迹方程为x2=8y.……………………………………2分
（II）由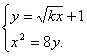
消去y并整理，
得
（III）逆命题：若=－12，则直线h过点B.为假命题.…………8分
此时直线h过点（0，2）或（0，6），故逆命题为假命题.…………12分
22．解：（I）该企业进行污染治理后的利润函数为
.………………3分
（II）
令
…………………………………………4分
①当
所以f(x)在[0，2]上为增函数，且
即当0<p≤时，对所有x∈
，都有
…………8分
②当2p>1，即<p<1时，e2p－1－1>0.
则当
时，
.…………………………11分
所以f(x)在（0，e2p－1）上为减函数，且<f(0)=0
则(x+1)ln(x+1)<2px.………………………………………………13分
综合可知，当0<p≤时，生产的第一季度始终不会出现亏损现象.……14分