第一讲 集合与函数
l 高考风向标
本讲的主要内容是:集合的有关概念和运算,含有绝对值的不等式及一元二次不等式的解法,逻辑关联词,四种命题,充要条件.映射的概念,函数的概念,函数的单调性,反函数的概念,分数指数幂的概念和性质,指数函数的图象和性质,对数的定义和运算性质,对数函数的图象与性质,函数的一些应用.
l 典型题选讲
例1 在![]() 中,“
中,“![]() ”是“
”是“![]() ”的什么条件?
”的什么条件?
讲解 在![]() 中,角A、B的对边分别是
中,角A、B的对边分别是![]()
![]() 是
是![]() 的外接圆的半径.
的外接圆的半径.
一方面,因为 A<B,所以a<b ,
即![]() ,亦即
,亦即 ![]() ,从而
,从而![]() 中
中
A<B![]()
![]() 。
。
另一方面,因为![]() ,
,
所以![]() ,即
,即 ![]() ,得A<B,
,得A<B,
从而![]() 中,
中,![]()
![]() A<B。
A<B。
故![]() 中,“
中,“![]() ”是“
”是“![]() ” 的充要条件.
” 的充要条件.
点评 试问:在![]() 中,“
中,“![]() ”是“
”是“![]() ”的什么条件?
”的什么条件?
例2 试构造一个函数![]() ,使得对一切
,使得对一切![]() 有
有![]() 恒成立,但是
恒成立,但是![]() 既不是奇函数又不是偶函数,则
既不是奇函数又不是偶函数,则![]() 可以是
.
可以是
.
讲解 ![]() 的图像部分关于原点对称,部分关于
的图像部分关于原点对称,部分关于![]() 轴对称,如
轴对称,如
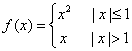 .
.
点评 本题是一道开放题,你能给出其它的答案吗?请不妨一试.
 例3 某种细胞分裂时,由1个分裂成2个,2个分裂成4个,…,一直分裂下去.
例3 某种细胞分裂时,由1个分裂成2个,2个分裂成4个,…,一直分裂下去.
(1) 用列表表示,1个细胞分裂1、2、3、4、5、6、7、8次后,得到的细胞个数;
(2)用图像表示1个细胞分裂的次数n(nÎN+)与得到的细胞个数y之间的关系;
(3)写出得到的细胞个数y与分裂次数n之间的关系式,试用计算器算算细胞分裂15次、20次得到的细胞个数.
讲解 (1) 利用正整指数幂的运算法则,可以算出1个细胞分裂1、2、3、4、5、6、7、8次后,得到的细胞个数,列表如下
| 分裂次数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 细胞个数 | 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 |
(2)细胞个数y与分裂次数n之间的关系式是
y=2n,nÎN+.
利用计算器可以算得
215=32768,220=.
故细胞分裂15次、20次得到的细胞个数分别是32768个和个.
点评 细胞分裂是一种很有趣的数学问题,我们也可以思考下面的类似的问题:
一种专门占据内存的计算机病毒,开机时占据内存![]() KB,然后每
KB,然后每![]() 分钟自身复制一次,复制后所占内存是原来的
分钟自身复制一次,复制后所占内存是原来的![]() 倍,那么开机后经过 ______ 分钟,该病毒占据
倍,那么开机后经过 ______ 分钟,该病毒占据![]() MB内存(
MB内存(![]() MB=
MB=![]() KB).
KB).
例4 已知函数![]() 的反函数
的反函数![]() ,
,![]()
(1)若![]() ,求
,求![]() 的取值范围
的取值范围![]() ;
;
(2)设函数![]() ,当
,当![]() 时,求
时,求![]() 的值域.
的值域.
讲解 ∵ ![]() ,
,
∴ ![]() .
.
(1)∵![]() 即
即![]() .
.
∴![]() ,
,
∴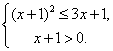
解之得 ![]() ,
,
∴![]() .
.
(2) ∵ ![]()
![]()
![]()
![]() .
. ![]()
令![]() ,显然在[0,1]递增,
,显然在[0,1]递增,
则有 ![]() .
.
∴![]() ,即
,即![]() 的值域为
的值域为![]() .
.
例5 某厂生产一种仪器,由于受生产能力和技术水平的限制,会产生一些次品.根据经验知道,该厂生产这种仪器,次品率![]() 与日产量
与日产量![]() (件)之间大体满足关系:
(件)之间大体满足关系:
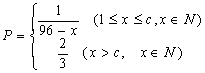 (其中c为小于96的正常数)
(其中c为小于96的正常数)
注:次品率![]() ,如
,如![]() 表示每生产10件产品,约有1件为次品.其余为合格品.
表示每生产10件产品,约有1件为次品.其余为合格品.
已知每生产一件合格的仪器可以盈利A元,但每生产一件次品将亏损![]() 元,故厂方希望定出合适的日产量.
元,故厂方希望定出合适的日产量.
(1)试将生产这种仪器每天的盈利额![]() (元)表示为日产量
(元)表示为日产量![]() (件)的函数;
(件)的函数;
(2)当日产量为多少时,可获得最大利润?
讲解 (1)当![]() 时,
时,![]() ,所以,每天的盈利额
,所以,每天的盈利额![]() ;
;
当![]() 时,
时,![]() ,所以,每日生产的合格仪器约有
,所以,每日生产的合格仪器约有![]() 件,次品约有
件,次品约有![]() 件.故,每天的盈利额
件.故,每天的盈利额
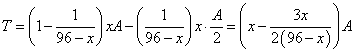 .
.
综上,日盈利额![]() (元)与日产量
(元)与日产量![]() (件)的函数关系为:
(件)的函数关系为:
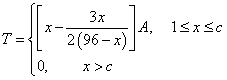
(2)由(1)知,当![]() 时,每天的盈利额为0.
时,每天的盈利额为0.
当![]() 时,
时,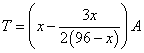 .
.
令![]() ,则
,则![]() .故
.故
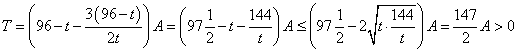 .当且仅当
.当且仅当![]() ,即
,即![]() 时,等号成立.
时,等号成立.
所以(i)当![]() 时,
时,![]() (等号当且仅当
(等号当且仅当![]() 时成立).
时成立).
(ii)
当![]() 时,由
时,由![]() 得
得![]() ,
,
易证函数![]() 在
在![]() 上单调递增(证明过程略).
上单调递增(证明过程略).
所以,![]() .所以,
.所以,
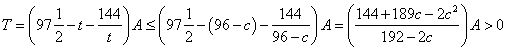 ,
,
即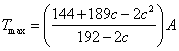 .(等号当且仅当
.(等号当且仅当![]() 时取得)
时取得)
综上,若![]() ,则当日产量为88件时,可获得最大利润;若
,则当日产量为88件时,可获得最大利润;若![]() ,则当日产量为
,则当日产量为![]() 时,可获得最大利润.
时,可获得最大利润.
点评 分段函数是历年高考的热门话题,常考常新,值得我们在复课时认真对待.
例6 设二次函数![]() ,已知不论α,β为何实数,恒有
,已知不论α,β为何实数,恒有
![]()
(1)求证:![]()
(2)求证:![]()
(3)若函数![]() 的最大值为8,求b,c的值.
的最大值为8,求b,c的值.
讲解 (1)由![]() 产生b+c,只要消除差异
产生b+c,只要消除差异![]() ,这可令
,这可令![]()
![]()
![]()
从而知 ![]()
(2)由![]()
又因为![]()
(3)![]()
当![]()
由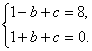 解得
解得 ![]()
点评 注意:![]() 且
且![]() , 这是用不等式证明等式的有效方法,很是值得重视.
, 这是用不等式证明等式的有效方法,很是值得重视.
例7 设f(x)=lg![]() ,a
,a![]() R, n
R, n![]() N且n
N且n![]() 2.若f(x)当x
2.若f(x)当x![]() (-
(-![]() ,1)有意义,求a的取值范围.
,1)有意义,求a的取值范围.
讲解 f(x)当x![]() (-
(-![]() ,1)有意义,当且仅当1+2
,1)有意义,当且仅当1+2![]() +…+(n-1)
+…+(n-1)![]() +an
+an![]() >0 对x
>0 对x![]() (-
(-![]() ,1)恒成立.即函数
,1)恒成立.即函数
g(x)=![]() +
+![]() +…+
+…+![]() +a>0
+a>0
对于任意的x![]() (-
(-![]() ,1)恒成立.
,1)恒成立.
因为g(x)在(-![]() ,1)上是减函数,其最小值为g(1)=
,1)上是减函数,其最小值为g(1)=
![]() +
+![]() +…+
+…+![]() +a=
+a=![]() (n-1)+a,
(n-1)+a,
所以g(x)
>0对x![]() (-
(-![]() ,1)恒成立的充要条件是
,1)恒成立的充要条件是![]() +a>0,即a>
+a>0,即a>![]() .
.
故所求实数a的范围为(![]() ,+
,+![]() ).
).
点评 构造函数是应用函数思想解题的基础,怎么构造,构造怎样的函数完全因题而定.请读者注意,恒成立问题在高考中多次出现,其解题方法,很值得探究.
例8 函数![]() 是定义在[0,1]上的增函数,满足
是定义在[0,1]上的增函数,满足![]() 且
且![]() ,在每个区间
,在每个区间![]() (
(![]() 1,2……)上,
1,2……)上,![]() 的图象都是斜率为同一常数k的直线的一部分.
的图象都是斜率为同一常数k的直线的一部分.
(1)![]() 及
及![]() ,
,![]() 的值,并归纳出
的值,并归纳出![]() 的表达式;
的表达式;
(2)直线![]() ,
,![]() ,x轴及
,x轴及![]() 的图象围成的矩形的面积为
的图象围成的矩形的面积为![]() (
(![]() 1,2……),记
1,2……),记![]() ,求
,求![]() 的表达式,并写出其定义域和最小值.
的表达式,并写出其定义域和最小值.
讲解 (1)为了求![]() ,只需在条件
,只需在条件![]() 中,令
中,令![]() ,即有
,即有
![]() ,得
,得![]() .
.
由![]() 及
及![]() ,得
,得![]() .
.
同理,![]() .
.
归纳得![]() .
.
(2)![]() 时,
时,
![]()
![]()
![]() .
.
故 ![]() 是首项为
是首项为![]() ,公比为
,公比为![]() 的等比数列,
的等比数列,
所以 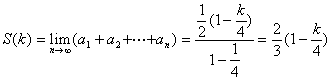 .
.
![]() 的定义域为
的定义域为![]() 1,当
1,当![]() 时取得最小值
时取得最小值![]() .
.
点评 本题是2004年北京高考数学第18题,将函数与数列综合在一起,体现了数学知识交汇性,是一道既知识、又考能力的活题.
l 针对性演练
1.合![]() ,若
,若![]() ,
,![]() ,则
,则![]() ,则运算
,则运算![]() 可能是 ( )
可能是 ( )
(A)加法 (B)减法 (C) 除法 (D)乘法
2.已知集合![]() ,
,![]() ,则满足条件
,则满足条件![]() 的映射
的映射![]() 的个数是 ( )
的个数是 ( )
(A)2 (B)4 (C)5 (D)7
3.某天清晨,小鹏同学生病了,体温上升,吃过药后感觉好多了,中午时他的体温基本正常,但是下午他的体温又开始上升,直到半夜才感觉身上不那么发烫了. 下面大致能上反映出小鹏这一天(0时—24时)体温的变化情况的图是
( )
 |
(A ) (B) (C) (D)
4.定义两种运算:![]()
![]() ,
,![]() ,则函数
,则函数![]() 为( )
为( )
(A)奇函数 (B)偶函数
(C)奇函数且为偶函数 (D)非奇函数且非偶函数
5.偶函数![]() 在
在![]() 上单调递增,则
上单调递增,则![]() 与
与![]() 的大小关系是 ( )
的大小关系是 ( )
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
6.已知函数![]()
![]() ,且正数C为常数.对于任意的
,且正数C为常数.对于任意的![]() ,存在一个
,存在一个![]() ,使
,使![]() ,则称函数
,则称函数![]() 在D上的均值为C. 试依据上述定义,写出一个均值为9的函数的例子:________________.
在D上的均值为C. 试依据上述定义,写出一个均值为9的函数的例子:________________.
7. 绿缘商店每月向工厂按出厂价每瓶3元购进一种饮料。根据以前的统计数据,若零售价定为每瓶4元,每月可销售400瓶;若每瓶售价每降低0.05元,则可多销售40瓶。请你给该商店设计一个方案:每月的进货量当月销售完,销售价应定为多少元和从工厂购进多少瓶时,才可获得最大的利润?
8.已知![]() 定义域为
定义域为![]() ,且对任意的
,且对任意的![]() 、
、![]() ,恒有
,恒有![]() ,
,![]() 时,
时,![]() .
.
(1)求![]() 的值,并证明
的值,并证明![]() ;
;
(2)求证:在![]() 的定义域内恒有
的定义域内恒有![]() .
.
9.已知定义域为[0,1]的函数f(x)同时满足:
(1)对于任意x∈[0,1],总有f(x)≥0;
(2)f(1)=1
(3)若![]() ,
,![]() ,
,![]() ,则有
,则有![]()
(Ⅰ)试求f(0)的值;
(Ⅱ)试求函数f(x)的最大值;
(Ⅲ)试证明:满足上述条件的函数f(x)对一切实数x,都有f(x)≤2x..
10. 设![]() 、
、![]() 为常数,
为常数,![]() :把平面上任意一点
:把平面上任意一点
(![]() ,
,![]() )映射为函数
)映射为函数![]()
(1)证明:不存在两个不同点对应于同一个函数;
(2)证明:当![]() 时,
时,![]() ,这里t为常数;
,这里t为常数;
(3)对于属于M的一个固定值![]() ,得
,得![]() ,在映射F的作用下,M1作为象,求其原象,并说明它是什么图象?
,在映射F的作用下,M1作为象,求其原象,并说明它是什么图象?
答案:
1.D.2.D.3.C.4.A.5.D.6.![]() ,
,![]() ,
, ![]() (
(![]() ).
).
7.450.8.略.
9.(I)令![]() ,
,
依条件(3)可得f(0+0) ≥f(0)+f(0),即f(0) ≤0.
又由条件(1)得f(0) ≥0,则f(0)=0.
(Ⅱ)任取![]() ,可知
,可知![]() ,
,
则![]() ,
,
即![]() ,故
,故![]()
于是当0≤x≤1时,有f(x)≤f(1)=1
因此,当x=1时,f(x)有最大值为1,
(Ⅲ)证明:
研究①当![]() 时,f(x) ≤1<2x
时,f(x) ≤1<2x
②当![]() 时,
时,
首先,f(2x) ≥f(x)+f(x)=2f(x),∴![]() .
.
显然,当![]() 时,
时,
![]() 成立.
成立.
假设当![]() 时,有
时,有![]() 成立,其中k=1,2,…
成立,其中k=1,2,…
那么当![]() 时,
时,
![]()
可知对于![]() ,总有
,总有![]() ,其中n=1,2,…
,其中n=1,2,…
而对于任意![]() ,存在正整数n,使得
,存在正整数n,使得![]() ,
,
此时![]() ,
,
③当x=0时,f(0)=0≤2x..
综上可知,满足条件的函数f(x),对x∈[0,1],总有f(x) ≤2x成立.
10. (1)假设有两个不同的点(![]() ,
,![]() ),(
),(![]() ,
,![]() )对应同一函数,即
)对应同一函数,即![]() 与
与![]() 相同,
相同,
即 ![]() 对一切实数x均成立。
对一切实数x均成立。
特别令x=0,得a=c;令![]() ,得b=d这与(a,b),(c,d)是两个不同点矛盾,假设不成立.
,得b=d这与(a,b),(c,d)是两个不同点矛盾,假设不成立.
故不存在两个不同点对应同函数。
(2)当![]() 时,可得常数a0,b0,使
时,可得常数a0,b0,使![]()
![]()
![]()
![]() 。
。
由于![]() 为常数,设
为常数,设![]() 是常数.
是常数.
从而![]() 。
。
(3)设![]() ,由此得
,由此得![]()
(![]() ,
,![]() )
)
在映射F下,![]() 的原象是(m,n),则M1的原象是
的原象是(m,n),则M1的原象是
![]()
消去t得![]() ,即在映射F下,M1的原象
,即在映射F下,M1的原象![]() 是以原点为圆心,
是以原点为圆心,![]() 为半径的圆.
为半径的圆.