2007届高三数学二轮复习新型题专题训练
一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 定义行列式运算:![]() ,将函数
,将函数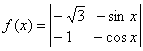 的图象向左平移m个单位
(m>0),所得图象对应的函数为偶函数,则m的最小值是
的图象向左平移m个单位
(m>0),所得图象对应的函数为偶函数,则m的最小值是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.以一个长方体的四个顶点为顶点的四面体中,四个面都是直角三角形的四面体有
A.8个 B.16个 C.24个 D.48个
3. 给出下列一系列化合物的分子式: ![]() 则该系列化合物中,分子中含碳元素的质量分数最大可无限接近
则该系列化合物中,分子中含碳元素的质量分数最大可无限接近
A. 95% B. 96% C. 97% D.98%
4.设M是![]() 内一点,且
内一点,且![]() ,定义
,定义![]() ,其中m、n、p分别是
,其中m、n、p分别是![]() 的面积,若
的面积,若![]() ,则
,则![]() 的最小值是
的最小值是
A.8 B.
5. 从一块短轴长为2b的椭圆形玻璃镜中划出一块面积最大的矩形,其面积的取值范围是[3b2,4b2],则这一椭圆离心率的取值范围是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6. 已知椭圆C:![]() 的右准线为l1,直线l2的方程为3x+4y—18=0.
若P是椭圆C上的点,P到l2、l1的距离分别为d1、d2,则d1+
的右准线为l1,直线l2的方程为3x+4y—18=0.
若P是椭圆C上的点,P到l2、l1的距离分别为d1、d2,则d1+![]() d2的最小值为
d2的最小值为
A.3
B.
7. 给定一条双曲线,过这条双曲线所在平面内的一点作n条直线,每条直线与双曲线有且只有一个交点,则n的所有可能的取值的集合为
A.{0,2} B.{0, 2, 4} C.{0, 2, 3, 4} D.{1, 2, 3, 4}
8. 正方体ABCD-A1B
A. ![]() B.
B. ![]() C.
C. ![]() D.
D.
![]()
9.已知![]() ={(x,y)x+y
={(x,y)x+y![]() 6,x
6,x![]() 0,y
0,y![]() 0},A={(x,y) x
0},A={(x,y) x![]() 4,y
4,y![]() 0,x-2y
0,x-2y![]() 0},若向区域
0},若向区域![]() 上随机投一点
上随机投一点![]() , 则点
, 则点![]() 落入区域
落入区域![]() 的概率为
的概率为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
 10.按ABO血型系统学说,每个人的血型为A,B,O,AB型四种之一,依血型遗传学,当且仅当父母中至少有一人的血型是AB型时,子女的血型一定不是O型,若某人的血型是O型,则其父母血型的所有可能情况有
10.按ABO血型系统学说,每个人的血型为A,B,O,AB型四种之一,依血型遗传学,当且仅当父母中至少有一人的血型是AB型时,子女的血型一定不是O型,若某人的血型是O型,则其父母血型的所有可能情况有
A.12
B.
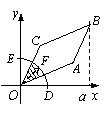
11.如图,圆弧型声波DFE从坐标原点O向外传播. 若D是DFE
弧与![]() 轴的交点,设
轴的交点,设![]()
![]() ),圆弧型声波DFE在
),圆弧型声波DFE在
传播过程中扫过平行四边形![]() 的面积为
的面积为![]() (图中阴影部分),
(图中阴影部分),
则函数![]() 的图象大致是
的图象大致是
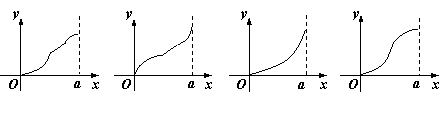 |
A. B. C. D.
| |
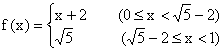 ,则
,则 A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
13.已知函数y=![]() x3+x2+x的图像C上存在一定点P满足:若过点p的直线l与曲线C交于不同于P的两点M(x1,y1),N(x2,y2),就恒有y1+y2为定值y0,则y0的值为
x3+x2+x的图像C上存在一定点P满足:若过点p的直线l与曲线C交于不同于P的两点M(x1,y1),N(x2,y2),就恒有y1+y2为定值y0,则y0的值为
 A.-
A.-![]() B.-
B.-![]() C.-
C.-![]() D.-2
D.-2
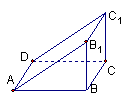
14.如图,直三棱柱ABB1—DCC1中,![]() ,
,
AB= 4,BC=2,CC1=1,DC上有一动点P,则![]() APC1
APC1
周长的最小值为
A.5+![]() B.5-
B.5-![]() C.4+
C.4+![]() D.4-
D.4-![]()
15.若m,n![]() ,其中
,其中![]() (i=0,1,2)
(i=0,1,2)![]() {1,2,3,4,5,6},并且m+n=
606,则实数对(m,n)表示平面上不同的点的个数为
{1,2,3,4,5,6},并且m+n=
606,则实数对(m,n)表示平面上不同的点的个数为
A.32个 B. 30个 C.62个 D.60个
16.一次研究性课堂上,老师给出函数![]() ,三位同学甲、乙、丙在研究此函数时分别给出命题:
,三位同学甲、乙、丙在研究此函数时分别给出命题:
甲:函数f (x)的值域为(-1,1); 乙:若x1≠x2,则一定有f (x1)≠f (x2);
丙:若规定![]() ,
,![]() 对任意
对任意![]() 恒成立. 你认为上述三个命题中正确的个数有
恒成立. 你认为上述三个命题中正确的个数有
A.0个 B.1个 C.2个 D.3个

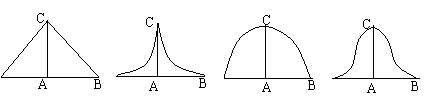 17.有一半径为R的圆柱,被与轴成45°角平面相截得“三角”圆柱ABC,则此“三角”圆柱的展开图为
17.有一半径为R的圆柱,被与轴成45°角平面相截得“三角”圆柱ABC,则此“三角”圆柱的展开图为
A. B. C. D.
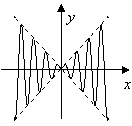 18.如图,虚线部分是四个象限的角平分线,实线部分是函数
18.如图,虚线部分是四个象限的角平分线,实线部分是函数
![]() 的部分图像,则
的部分图像,则![]() 可能是:
可能是:
A.![]() B.
B.![]()
C.![]() D.
D.![]()
19.国际上常用恩格尔系数(恩格尔系数=![]() )来
)来
衡量一个国家和地区人民生活水平的状况。根据联合国粮农
组织提出的标准,恩格尔系数在60%以上为贫困,50%~60%为温饱,40%~50%为小康,30%~40%为富裕,低于30%为最富裕。一个地区今年刚好脱贫,以后每年食物支出金额和总支出金额分别以5%和10%的年增长率递增,如果该地区的生活水平要达到富裕,那么至少需要(可参考![]() 的二项展开式进行估算)
的二项展开式进行估算)
A.5年 B.7年 C.9年 D.11年
20.根据表格中的数据,可以判定方程![]() 的一个根所在的区间为
的一个根所在的区间为
| x | -1 | 0 | 1 | 2 | 3 |
|
| 0.37 | 1 | 2.72 | 7.39 | 20.09 |
|
| 1 | 2 | 3 | 4 | 5 |
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
21.一个三棱锥的三个侧面中有两个是等腰直角三角形,另一个是边长为1的正三角形,那么这个三棱锥的体积大小
A.有唯一确定的值 B.有2不同的值
C.有3个不同的值 D.有3个以上不同的值
22.函数![]() (
(![]() )是常数,其图象是一条直线,称这个函数为线性函数.对于非线性可导函数
)是常数,其图象是一条直线,称这个函数为线性函数.对于非线性可导函数![]() ,在点
,在点![]() 附近一点
附近一点![]() 的函数值
的函数值![]() ,可以用如下方法求其近似代替值:
,可以用如下方法求其近似代替值:
![]() .
.
利用这一方法,![]() 的近似代替值
的近似代替值
A.大于![]() B.小于
B.小于![]() C.等于
C.等于![]() D.与
D.与![]() 的大小关系无法确定
的大小关系无法确定
23.若m、n均为非负整数,在做m+n的加法时各位均不进位(例如,134+3802=3936),则称(m,n)为“简单的”有序对,而m+n称为有序数对(m,n)的值,那么值为1942的“简单的”有序对的个数是
A.20
B.
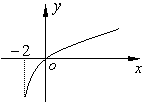 24.已知函数
24.已知函数![]() 的定义域为
的定义域为![]() ,部分对应值如下表.
,部分对应值如下表.![]() 为
为![]() 的导函数,函数
的导函数,函数![]() 的图象如下图所示.
的图象如下图所示.
|
|
|
|
|
|
|
|
|
|
若两正数![]() 满足
满足![]() ,则
,则![]() 的取值范围是
的取值范围是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
25.已知![]() 中 ,角A,B,C的对边分别为a,b,c,AH为BC边上有高,以下结论:①
中 ,角A,B,C的对边分别为a,b,c,AH为BC边上有高,以下结论:①![]() ;②
;②![]() 为锐角三角形③
为锐角三角形③![]()
![]() ;④
;④![]() ,其中正确的个数是
,其中正确的个数是
A.1
B.
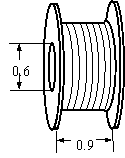 26. 电缆绕在圆柱形的架子上,如图,若空架时架芯直径为
26. 电缆绕在圆柱形的架子上,如图,若空架时架芯直径为
满架时直径为
则满架时所绕的电缆的长是(按电缆的中心线计算各圈的长
度,π取3)
A.
C.
27.如图一圆形纸片的圆心为O,F是圆内一定点,M是圆周
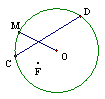 上一动点,把纸片折叠使M与F重合,然后抹平纸片,折
上一动点,把纸片折叠使M与F重合,然后抹平纸片,折
痕为CD,设CD与OM交于P,则点P的轨迹是
A.椭圆 B.双曲线
C.抛物线 D.圆
28. 若实数x,y满足![]() 则
则![]() 的最小值为
的最小值为
A.3
B.![]() C.
C.![]() D.
D.![]()
29.已知实数a,b均不为零,![]() ,且
,且![]() ,则
,则![]() 等于
等于
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
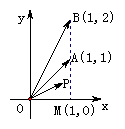 30.如图,点P在
30.如图,点P在![]() OMA上或它的内部运动,且
OMA上或它的内部运动,且![]() x
x![]()
+ y![]() (x,y
(x,y![]() R),当y取最大值时,x的取值范围是
R),当y取最大值时,x的取值范围是
A.![]() B.
B.![]()
C.![]() D.
D.![]()
31.称![]() 为两个向量
为两个向量![]() 、
、![]() 间的“距离”.若向量
间的“距离”.若向量
![]() 、
、![]() 满足:①
满足:①![]() ;②
;②![]() ;③对任意的
;③对任意的![]() ,恒有
,恒有
![]() 则
则
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
32.已知双曲线![]() 的左、右顶点分别为A、B,双曲线在第一象限的图像上有一点P,
的左、右顶点分别为A、B,双曲线在第一象限的图像上有一点P,![]() ,则
,则
A.![]() B.
B.![]()
C.![]() D.
D.![]()
二、填空题:本大题每小题5分,把答案填在题中横线上。
1.根据绝对值的几何意义可求得:函数![]() 的最小值为0;函数
的最小值为0;函数![]() +
+![]() 的最小值为1;函数
的最小值为1;函数![]() +
+![]() 的最小值为2.则函数
的最小值为2.则函数
![]() +
+![]() 的最小值为______________.答案:56
的最小值为______________.答案:56
2.已知![]() 均为实数),请推测a=
,b= .
答案:a=6 b=35
均为实数),请推测a=
,b= .
答案:a=6 b=35
3.考察下列一组不等式:
![]() .
.
将上述不等式在左右两端仍为两项和的情况下加以推广,使以上的不等式成为推广不等式的特例,则推广的不等式可以是___________________.
3.答案:![]() (或
(或![]() 为正整数).注:填
为正整数).注:填![]() 以及是否注明字母的取值符号和关系,均不扣分;
以及是否注明字母的取值符号和关系,均不扣分;
若填![]() 或
或![]() 可给3分.
可给3分.
4. 一次单元测试由50个选择题构成,每个选择题有4个选项,其中恰有一个是正确的答案,每题选择正确得3分,不选或选错得0分,满分150分.学生甲选对任一题的概率为0.8,则该生在这次测试中成绩的期望值是_________,标准差是_____________. 答案:120,
![]()
5. 椭圆![]() 的长轴为A
的长轴为A![]() _____________.答案:
_____________.答案:![]() , 8
, 8
6.我们知道:“过圆为![]() 的圆外一点
的圆外一点![]() 作它的两条切线
作它的两条切线![]() 、
、![]() ,其中
,其中![]() 、
、![]() 为切点,则
为切点,则![]() .”这个性质可以推广到所有圆锥曲线,请你写出其中一个:
.”这个性质可以推广到所有圆锥曲线,请你写出其中一个:
.
6.答案:①过抛物线![]() (
(![]() )外一点
)外一点![]() 作抛物线的两条切线
作抛物线的两条切线![]() 、
、![]() (
(![]() 、
、![]() 为切点),若
为切点),若![]() 为抛物线的焦点,则
为抛物线的焦点,则![]() .(如果学生写出的是抛物线的其它方程,只要正确就给满分)
.(如果学生写出的是抛物线的其它方程,只要正确就给满分)
②过椭圆![]() (
(![]() )外一点
)外一点![]() 作椭圆的两条切线
作椭圆的两条切线![]() 、
、![]() (
(![]() 、
、![]() 为切点),若
为切点),若![]() 为椭圆的一个焦点,则
为椭圆的一个焦点,则![]() .(如果学生写出的是椭圆的其它方程,只要正确就给满分)
.(如果学生写出的是椭圆的其它方程,只要正确就给满分)
③过双曲线![]() (
(![]() )外(两支之间)一点
)外(两支之间)一点![]() (
(![]() 不在渐近线上)作双曲线的两条切线
不在渐近线上)作双曲线的两条切线![]() 、
、![]() (
(![]() 、
、![]() 为切点),设
为切点),设![]() 为双曲线的一个焦点.⑴若
为双曲线的一个焦点.⑴若![]() 、
、![]() 在同一支,则
在同一支,则![]() ;⑵若
;⑵若![]() 、
、![]() 不在同一支,则
不在同一支,则![]() 平分
平分![]() 的邻补角.(如果学生写出的是双曲线的其它方程,只要正确就给满分)
的邻补角.(如果学生写出的是双曲线的其它方程,只要正确就给满分)
7. 设![]() ,
,
![]() ,求
,求![]() =___________ . 答案:
1
=___________ . 答案:
1
8.9.(从给出的三道选做题中选择其中两道作答)

![]() ① 如图,圆内的两条弦
① 如图,圆内的两条弦![]() 、
、![]() 相交于圆内一点P,
相交于圆内一点P,
已知![]() ,则
,则![]()
② 已知点![]() 上的点,则
上的点,则
![]() 的最大值是
的最大值是
③ 函数![]() 的最大值是
.
的最大值是
.
答案:① ![]() ② 2b
③ 5
② 2b
③ 5
10.设全集![]() , 集合
, 集合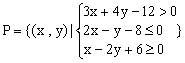 ,
,
![]() ,若
,若![]() 恒成立,则实数r的最大值为___.
恒成立,则实数r的最大值为___.
答案:![]()
11.有以下四个命题(![]() ):(1) n = n+1;
(2)
):(1) n = n+1;
(2) ![]() ; (3) 2+4+6+…+2n = n2+n+2; (4) 凸n边形对角线的条数
; (3) 2+4+6+…+2n = n2+n+2; (4) 凸n边形对角线的条数 ![]() .
.
其中满足“假设![]() 时命题成立,则当n=k+1时命题也成立”,但不满足“当n=
时命题成立,则当n=k+1时命题也成立”,但不满足“当n=![]() (
(![]() 是题中给定的n的初始值)时命题成立”的命题序号是_____.
是题中给定的n的初始值)时命题成立”的命题序号是_____.
答案:(1) (3)
12.按下列程序框图来计算:

如果x=5,应该运算 次才停止. 答案: 4
13.对一切实数x,令为 [ x ]不大于x的最大整数,则函数f(x)= [ x ]称为高斯函数或取整函数.
(1)计算 f (-0.3)+f (1)+f (1.3)=___________ ;
(2)若![]() ,n
,n![]() N*,
N*,![]() 为数列{a n}的前n项和,则
为数列{a n}的前n项和,则![]() =____________ .
=____________ .
答案:1;![]()
14.在如图所示的九宫格中,用红、黄、蓝三种颜色涂其中三格,
每种颜色只涂一格,且红色不与另外两种颜色相邻(有公共边
的方格称为相邻),则不同的涂法种数为 .(用数字
作答) 答案: 212
15.在斜坐标系xOy中,![]()
![]() 分别是x轴,y轴的单位向量.对于坐标平面内
分别是x轴,y轴的单位向量.对于坐标平面内
| |
(1)已知P的斜坐标为(![]() ,1),则
,1),则![]() .
.
(2)在此坐标平面内,以O为原点,半径为1的圆的方程是 .
答案:![]() ;
;![]()
16. 有这样一首诗:“有个学生资性好,一部《孟子》三日了,每日添增一倍多,问君每日读多少?”(注:《孟子》全书共34685字,“一倍多”指一倍),由此诗知该君第二日读的字数为 . 答案: 9910
17. 已知A(-1,0),B(2,1),C(1,-1).若将坐标平面沿x轴折成直二面角,则折后![]() 的余弦值为 . 答案:
的余弦值为 . 答案: ![]()
18. 已知直线![]() 和平面
和平面![]() ,试利用上述三个元素并借助于它们之间的位置关系,构造出一个判断
,试利用上述三个元素并借助于它们之间的位置关系,构造出一个判断![]() ⊥
⊥![]() 的真命题 .
的真命题 .
18. 答案: ![]()
![]() ⊥
⊥![]() 或
或 ![]()
![]() ⊥
⊥![]()
19.试构造一个函数![]() ,使得对一切
,使得对一切![]() 有
有![]() 恒成立,但是
恒成立,但是![]() 既不是奇函数又不是偶函数,则
既不是奇函数又不是偶函数,则![]() 可以是
.
可以是
.
答案:![]() 的图像部分关于原点对称,部分关于
的图像部分关于原点对称,部分关于![]() 轴对称,如
轴对称,如 .
.
20.代号为“狂飙”的台风于某日晚8点在距港口的A码头南偏东60°的400千米的海面上形成,预计台风中心将以
三、解答题:本大题解答应写出文字说明,证明过程或演算步骤.
1. 已知向量![]() ,
,![]() ,动点M到定直线y=1的距离等于d,并且满足
,动点M到定直线y=1的距离等于d,并且满足![]() ,其中O为坐标原点,k为参数.
,其中O为坐标原点,k为参数.
(1)求动点M的轨迹方程,并判断曲线类型;
(2)如果动点M轨迹是一条圆锥曲线,其离心率e满足![]() ,求实数k的取值范围.
,求实数k的取值范围.
1. 简要答案:(1)所求方程为(1—k)x2 +2(k—1)x+y2 = 0
若k=1时,轨迹为一条直线;若k=0,则为圆;若k>1,则为双曲线;若0<k<1或k<0,则为椭圆.
(2) 当![]() 时,方程为
时,方程为![]() ,表示椭圆,分0<k<1或k<0两种情况,可求得
,表示椭圆,分0<k<1或k<0两种情况,可求得![]() .
.
2. 求出一个数学问题的正确结论后,将其作为条件之一,提出与原来问题有关的新问题,我们把它称为原来问题的一个“逆向”问题.
例如,原来问题是“若正四棱锥底面边长为4,侧棱长为3,求该正四棱锥的体积”.求出体积![]() 后,它的一个“逆向”问题可以是“若正四棱锥底面边长为4,体积为
后,它的一个“逆向”问题可以是“若正四棱锥底面边长为4,体积为![]() ,求侧棱长”;也可以是“若正四棱锥的体积为
,求侧棱长”;也可以是“若正四棱锥的体积为![]() ,求所有侧面面积之和的最小值”.
,求所有侧面面积之和的最小值”.
试给出问题“在平面直角坐标系xoy中,求点![]() 到直线
到直线![]() 的距离.”的一个有意义的“逆向”问题,并解答你所给出的“逆向”问题.
的距离.”的一个有意义的“逆向”问题,并解答你所给出的“逆向”问题.
2. 评分说明:(ⅰ) 在本题的解答过程中,如果考生所给问题的意义不大,那么在评分标准的第二阶段所列6分中,应只给2分,但第三阶段所列4分由考生对自己所给问题的解答正确与否而定.
(ⅱ) 当考生所给出的“逆向”问题与所列解答不同,可参照所列评分标准进行评分.
[解] 点![]() 到直线
到直线![]() 的距离为
的距离为![]() .
…… 4分
.
…… 4分
“逆向”问题可以是:
(1) 求到直线![]() 的距离为2的点的轨迹方程.
…… 10分
的距离为2的点的轨迹方程.
…… 10分
[解] 设所求轨迹上任意一点为![]() ,则
,则![]() ,
,
所求轨迹为![]() 或
或![]() .
…… 14分
.
…… 14分
(2) 若点![]() 到直线
到直线![]() 的距离为2,求直线
的距离为2,求直线![]() 的方程. … 10分
的方程. … 10分
[解] ![]() ,化简得
,化简得![]() ,
,![]() 或
或![]() ,
,
所以,直线![]() 的方程为
的方程为![]() 或
或![]() .
…… 14分
.
…… 14分
意义不大的“逆向”问题可能是:
(3) 点![]() 是不是到直线
是不是到直线![]() 的距离为2的一个点? …… 6分
的距离为2的一个点? …… 6分
[解] 因为![]() ,
,
所以点![]() 是到直线
是到直线![]() 的距离为2的一个点.
……10分
的距离为2的一个点.
……10分
(4) 点![]() 是不是到直线
是不是到直线![]() 的距离为2的一个点? …… 6分
的距离为2的一个点? …… 6分
[解] 因为![]() ,
,
所以点![]() 不是到直线
不是到直线![]() 的距离为2的一个点.
……10分
的距离为2的一个点.
……10分
(5) 点![]() 是不是到直线
是不是到直线![]() 的距离为2的一个点? …… 6分
的距离为2的一个点? …… 6分
[解] 因为![]() ,
,
所以点![]() 不是到直线
不是到直线![]() 的距离为2的一个点. ……10分
的距离为2的一个点. ……10分
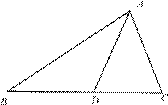
3. 田忌和齐王赛马是历史上有名的故事,设齐王的三匹马分别为A1、A2、A3;田忌的三匹马B1、B2、B3;三匹马各比赛一次,胜两场者为获胜,双方均不知对方的马出场顺序。
(1)若这六匹马比赛优、劣程度可以用不等式表示:A1>B1>A2>B2>A3>B3;则田忌获胜的概率是多大?
(2)若这六匹马比赛优、劣程度可以用不等式表示:A1>B1>A2>B2>B3>A3;则田忌获胜的概率是多大?
3. 解:(1)田忌获胜的概率是![]() ;
;
(2)田忌获胜的概率是![]() 。
。
 4.在
4.在![]() 中,
中,![]() .
.
(1) 证明:![]() ;
;
(2) 若![]() , 求
, 求![]() 的值.
的值.
4. 解:(1)设![]() ,则
,则
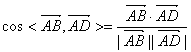 =
=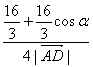 ,
,
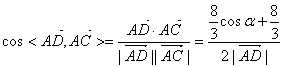 ,
,
![]() ,
,
又![]() ,
,
![]() .
.
(2) ![]()
=![]() ,
,![]()
![]()
![]()
![]()
|
| 耐 磨 度 | |||||
| 5 | 4 | 3 | 2 | 1 | ||
| 硬 度 | 5 | 1 | 3 | 1 | 0 | 0 |
| 4 | 1 | 0 | 7 | 5 | 1 | |
| 3 | 2 | 1 | 0 | 9 | 3 | |
| 2 | 1 | 2 | 6 | 0 | 1 | |
| 1 | 0 | 0 | 1 | 1 | 3 | |
5.某研究所试制出一大批特种陶瓷刀,他们从这批产品中随机抽取了50个样本,检测它们的硬度和耐磨度.硬度和耐磨度各分为5个档次,检测结果如下表.如表中所示硬度为5、耐磨度为4的刀具有3把.若在该批产品中任选一把刀具,其硬度记为![]() ,耐磨度记为
,耐磨度记为![]() .
.
(1)试根据这50个样本估计![]() 的概
的概
率是多少?![]() 且
且![]() 的概率是多少?
的概率是多少?
(2)若从这一大批产品中任 意取出3把
刀具,则这3把刀具至少有2把的耐磨度
为5的概率是多少?
(3)根据这50个样本估计![]() 的期望值.
的期望值.
5. 解:(1) ![]()
![]()
(2)由(1)可知,任取1把刀具,其耐磨度为5的概率![]() ,故任取3把,至少有2把耐磨度为5的概率为
,故任取3把,至少有2把耐磨度为5的概率为![]() ;
;
(3)由题意可知![]() 的分布列为
的分布列为
|
| 5 | 4 | 3 | 2 | 1 |
|
|
|
|
|
|
|
![]() .
.
6. 设F(x)=![]() (0<x<1)
(0<x<1)
(1)求F(x)的最小值.
(2)设p、q、r为正数,且2p=q+r,q≠r,试证明![]() <
<![]()
6. 解:(1)令G(x)=![]() .
.
![]()
令![]()
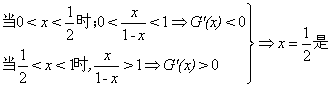 G(x)的极小值,
G(x)的极小值,
也是最小值,![]()
(2)由(1)知,当0<x<1且![]() ……①
……①
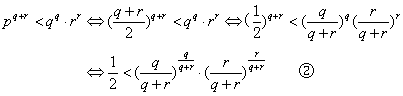
令![]() ∵q≠r,∴x≠
∵q≠r,∴x≠![]()
不等式②即为:![]() 由①可知,证毕.
由①可知,证毕.
7. 在数列![]() 中,
中,![]()
(Ⅰ)试比较![]() 与
与![]() 的大小;
的大小;
(Ⅱ)证明:当![]() 时,
时,![]() .
.
7. 解:(Ⅰ)由题设知,对任意![]() ,都有
,都有![]()
![]() ,
,
![]()
![]()
![]() ………………………………6分
………………………………6分
(Ⅱ)证法1:由已知得,![]()
![]() 又
又![]() .
.
当![]() 时,
时,![]()
![]()
![]()
![]() …………………………………10分
…………………………………10分
设![]() ①
①
则![]() ②
②
①-②,得
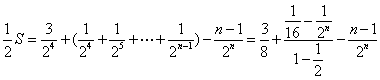
![]()
![]() ……………………14分
……………………14分
证法2:由已知得,![]()
(1) 当![]() 时,由
时,由![]() ,知不等式成立。………8分
,知不等式成立。………8分
(2) 假设当![]() 不等式成立,即
不等式成立,即![]() ,那么
,那么
![]()
要证 ![]() ,只需证
,只需证![]()
即证 ![]() ,则只需证
,则只需证![]() ………………10分
………………10分
因为![]() 成立,所以
成立,所以![]() 成立.
成立.
这就是说,当![]() 时,不等式仍然成立.
时,不等式仍然成立.
根据(1)和(2),对任意![]() ,且
,且![]() ,都有
,都有![]() ……14分
……14分
8.
杨辉是中国南宋末年的一位杰出数学家、数学教育家,他的数学著作颇多,他编著的数学书共5种21卷.在他的著作中收录了不少现已失传的古代数学著作中的算题和 算法.他的数学研究与教育工作的重点是在计算技术方面.杨辉三角是杨辉的一大重要研究成果.它的许多性质与组合数的性质有关.杨辉三角中蕴涵了许多优美的规律,古今中外,许多数学家如贾宪、先世杰、帕斯卡、华罗庚等都曾深入研究过,并将研究结果应用于其他工作,如图是一个11阶的杨辉三角,试回答:(其中第(Ⅰ)~(Ⅴ)小题只须直接给出最后的结果,无须求解过程)
算法.他的数学研究与教育工作的重点是在计算技术方面.杨辉三角是杨辉的一大重要研究成果.它的许多性质与组合数的性质有关.杨辉三角中蕴涵了许多优美的规律,古今中外,许多数学家如贾宪、先世杰、帕斯卡、华罗庚等都曾深入研究过,并将研究结果应用于其他工作,如图是一个11阶的杨辉三角,试回答:(其中第(Ⅰ)~(Ⅴ)小题只须直接给出最后的结果,无须求解过程)
(Ⅰ)记第![]() 行中从左到右的第
行中从左到右的第![]() 个数为
个数为![]() ,则数列
,则数列![]() 的通项公式为 ;
的通项公式为 ;![]() 阶杨辉三角中共有
个数.
阶杨辉三角中共有
个数.
(Ⅱ)第![]() 行各数的和是
.
行各数的和是
.
(Ⅲ)![]() 阶杨辉三角的所有数的和是
.
阶杨辉三角的所有数的和是
.
(Ⅳ)将第![]() 行的所有数按从左到右的顺序合并在一起得到的多位数等于 .
行的所有数按从左到右的顺序合并在一起得到的多位数等于 .
(Ⅴ)第![]() 行除去两端的数字1以外的所有数都能被
行除去两端的数字1以外的所有数都能被![]() 整除,则整数
整除,则整数![]() 一定为 (在下面选项中选择一个你认为正确的代号)。
一定为 (在下面选项中选择一个你认为正确的代号)。
A. 奇数 B. 质数 C. 非偶数 D. 合数
(Ⅵ)在第3斜列中,前5个数依次为1、3、6、10、15;第4斜列中,第5个数 为35,显然1+3+6+10+15=35.事实上,一般地有这样的结论:
第![]() 斜列中(从右上至左下)前
斜列中(从右上至左下)前![]() 个数之和,一定等于第
个数之和,一定等于第![]() 斜列中第
斜列中第![]() 个数.试用含有
个数.试用含有![]() 、
、![]() (
(![]() )的数学公式表示上述结论并证明其正确性.
)的数学公式表示上述结论并证明其正确性.
8. 解:(1)![]()
(6)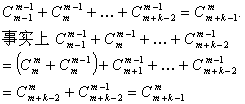
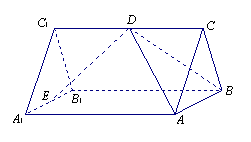 9. 如图,已知
9. 如图,已知![]() 是正三棱柱,它的底面边长和侧棱长都是2,D为侧棱
是正三棱柱,它的底面边长和侧棱长都是2,D为侧棱![]() 的中点,
的中点,![]() 为
为![]() 的中点.
的中点.
(1)求证:![]() ;
;
(2)求直线![]() 到平面
到平面![]() 的距离;
的距离;
(3)求二面角![]() 的大小.
的大小.
9. (1)证明: 连结C1E,则C1E^A1B1,
又∵A1B1^C1C,∴A1B1^平面EDC1,∴A1B1^DE,
而A1B1//AB,∴AB^DE. ·························································5分
(2) 取AB中点为F,连结EF、DF,则EF^AB,∴AB^DF.
过E作直线EH^DF于H点,则EH^平面DAB,∴EH就是直线A1B1到平面DAB的距离. 在矩形C1EFC中,∵AA1=AB=2,∴EF=2,C1E=,DF=2,
∴在△DEF中,EH=,
故直线A1B1到平面DAB的距离为. ·····························10分
(3) 过A作AM^BC于M点,则AM^平面CDB,
过M作MN^BD于N点,连结AN,则AN^BD,
∴∠ANM即为所求二面角的平面角,
在Rt△DCB中,BC=2,DC=1,M为BC中点,∴MN=,
在Rt△AMN中,tan∠ANM=,
故二面角A-BD-C的大小为arctan. ·································15分
10. 某厂拟生产甲、乙两种试销产品,每件销售收入分别为3千元、2千元. 甲、乙产品都需要在A,B两种设备上加工,在每台A,B上加工一件甲所需工时分别为1工时、2工时,加工一件乙所需工时分别为2工时、1工时,A,B两种设备每月有效使用台时数为![]()
![]() . 求生产收入最大值的范围?
. 求生产收入最大值的范围?
10. 解: 设甲、乙两种产品月的产量分别为![]() ,
,![]() 件,
1分
件,
1分
约束条件是 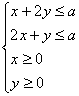
目标函数是![]() ------------ 4分
------------ 4分
由约束条件画出可行域,如图(略). ------ 6分
将![]() 它变形为
它变形为![]() ,
,
这是斜率为![]() 、随
、随![]() 变化的一簇直线.
变化的一簇直线.![]() 是直线在
是直线在![]() 轴上的截距,当
轴上的截距,当![]() 最大时
最大时![]() 最大,当然直线要与可行域相交,即在满足约束条件时目标函数取得最大值.
最大,当然直线要与可行域相交,即在满足约束条件时目标函数取得最大值.
由![]() 解得
解得 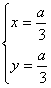 -------------------- 8分
-------------------- 8分
在这个问题中,使![]() 取得最大值的
取得最大值的![]() 是两直线
是两直线![]() 与
与![]() 的交点
的交点![]() .
.
∴ ![]() --------------------- 10分
--------------------- 10分
又∵ ![]()
∴ ![]() --------------------- 11分
--------------------- 11分
答:月生产收入最大值的范围是![]() . ---------------------
12分
. ---------------------
12分
 11.把正整数按上小下大,左小右大的原则排成三角形数表示(每一行比上一行多一个数), 如右图所示:设
11.把正整数按上小下大,左小右大的原则排成三角形数表示(每一行比上一行多一个数), 如右图所示:设![]() 是位于这个三角形数表中从上往下数第
是位于这个三角形数表中从上往下数第![]() 行,从左往右数第
行,从左往右数第![]() 个数,如
个数,如![]() .
.
(1)若![]() ,求
,求![]() 的值;
的值;
(2)记三角形数表从上往下数第n行各数之和为![]() ,
,
令,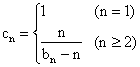 ,若数列
,若数列![]() 的前
的前![]() 项和为
项和为![]() ,
,
求![]() 的值.
的值.
11.解:①∵![]()
又∵![]() ,
,![]() ∴
∴![]() …………………….3分
…………………….3分
又∵![]() ∴
∴![]() ………6分
………6分
②![]()
![]() …9分
…9分
当![]() 时
时
∴![]()
![]() ………………………………11分
………………………………11分
∴![]()
![]() …………………………………………………….12分
…………………………………………………….12分
12. 已知各项均为正数的数列{a n}满足 ![]() ,
,![]() ,其中n
,其中n![]() N*.
N*.
(1)求a1和a2的值;
(2)求证:![]() ;
;
(3)求证:![]() .
.
12. 简要答案:(1)![]() ,
,![]() ;
;
(2)由已知可得,![]() ,所以有
,所以有
![]() ,即得
,即得![]() ;
;
(3)把(2)的结果累加有![]() ,于是,
,于是,![]() ;
;
![]() ,于是,
,于是,
![]() ,
,![]() ,得
,得
![]() ,对前式累加得,
,对前式累加得,
![]() ,得,
,得,![]() ,
,![]() .
.
13.已知点P在曲线C:![]() 上,曲线C在点P处的切线与函数y=kx(k>0)的图象交于点A,与x轴交于点B,设点P的横坐标为t,点A、B的横坐标分别为xA、xB,设f(t)=xA·xB.
上,曲线C在点P处的切线与函数y=kx(k>0)的图象交于点A,与x轴交于点B,设点P的横坐标为t,点A、B的横坐标分别为xA、xB,设f(t)=xA·xB.
(1)求f(t)的解析式;
(2)设数列![]() 的通项公式;
的通项公式;
(3)在(2)的条件下,当1<k<3时,证明不等式: ![]()
| |
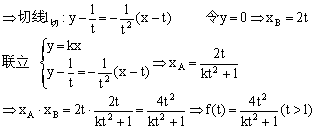
(2)![]()
① 若k=3时,![]() 是以0为前项的常数数列
是以0为前项的常数数列![]() an=1
an=1
② 若k≠3时,数列![]() 为公比的等比数列
为公比的等比数列
![]()
综合①②得![]()
(3)证明: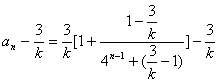
![]()
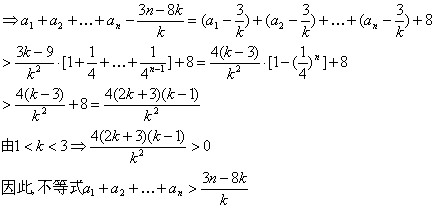
14.已知a>1,数列{an}的通项公式是an =![]() ,前n项和记作Sn(n = 1,2,…),规定S0 = 0. 函数f(x)在S0处和每个区间
,前n项和记作Sn(n = 1,2,…),规定S0 = 0. 函数f(x)在S0处和每个区间![]() (i = 0,1,2,…)上有定义,且f(S0)= 0,f(Si)= ai(i = 1,2,…).当x∈(Si,Si+1)时,f(x)的图像完全落在连结点Pi(Si,f(Si))与点Pi+1(Si+1,f(Si+1))的线段上.
(i = 0,1,2,…)上有定义,且f(S0)= 0,f(Si)= ai(i = 1,2,…).当x∈(Si,Si+1)时,f(x)的图像完全落在连结点Pi(Si,f(Si))与点Pi+1(Si+1,f(Si+1))的线段上.
(Ⅰ)求f(x)的定义域;
(Ⅱ)设f(x)的图像与坐标轴及直线l :x = Sn(n = 1,2,…)围成的图形面积为An,求An及![]() ;
;
(Ⅲ)若存在正整数n,使得An>a2,求a的取值范围.
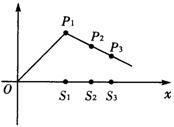
14. 解:(Ⅰ)f (x)的定义域是{S0}∪![]() ,
,
由于所有的an都是正数,故Sn是单调递增的.
 ∵
∵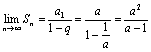
∴f
(x)的定义域是![]() .
.
(Ⅱ)∵![]()
=![]() 与i无关.
与i无关.
∴所有的P1,P2,P3 …共线,该直线过点P1(a,a),斜率为1-a,
∴A1 =![]()
当n≥2时,An是一个三角形与一个梯形面积之和(如上图所示).
![]()
=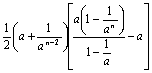 =
=![]()
于是An =![]() ,故
,故![]()
15.有一种密码,明文是由三个字符组成,密码是由明文对应的五个数字组成,编码规则如下表:明文由表中每一排取一个字符组成,且第一排取的字符放在第一位,第二排取的字符放在第二位,第三排取的字符放在第三位,对应的密码由明文对应的数字按相同的次序排成一组成.
| 第一排 | 明文字符 | A | B | C | D |
| 密码字符 | 11 | 12 | 13 | 14 | |
| 第二排 | 明文字符 | E | F | G | H |
| 密码字符 | 21 | 22 | 23 | 24 | |
| 第三排 | 明文字符 | M | N | P | Q |
| 密码字符 | 1 | 2 | 3 | 4 |
设随机变量ξ表示密码中不同数字的个数.
(Ⅰ)求P(ξ=2)
(Ⅱ)求随机变量ξ的分布列和它的数学期望.
15.解:(Ⅰ)密码中不同数字的个数为2的事件为密码中只有两个数字,注意到密码的第1,2列分别总是1,2,即只能取表格第1,2列中的数字作为密码.
![]() …………………………………………4分
…………………………………………4分
(Ⅱ)由题意可知,ξ的取值为2,3,4三种情形.
若ξ= 3,注意表格的第一排总含有数字1,第二排总含有数字2则密码中只可能取数字1,2,3或1,2,4.
![]()
若![]()
(或用![]() 求得). ………………………………8分
求得). ………………………………8分
![]() 的分布列为:
的分布列为:
| ξ | 2 | 3 | 4 |
| p |
|
|
|
![]() ……………………………12分
……………………………12分
16.设无穷数列{an}具有以下性质:①a1=1;②当![]()
(Ⅰ)请给出一个具有这种性质的无穷数列,使得不等式![]() 对于任意的
对于任意的![]() 都成立,并对你给出的结果进行验证(或证明);
都成立,并对你给出的结果进行验证(或证明);
(Ⅱ)若![]() ,其中
,其中![]() ,且记数列{bn}的前n项和Bn,证明:
,且记数列{bn}的前n项和Bn,证明:![]()
16.解:(Ⅰ)令![]() ,
,
则无穷数列{an}可由a1 = 1,![]() 给出.
给出.
显然,该数列满足![]() ,且
,且
![]() …………6分
…………6分
(Ⅱ)![]()
![]() ……………………………………8分
……………………………………8分
又![]()
![]()
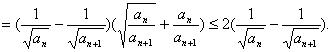
![]()
![]()
17. 已知点![]() 都在椭圆
都在椭圆![]() 上,
上,![]() 、AC分别过两个焦点
、AC分别过两个焦点![]() ,当
,当![]() 时,有
时,有![]() 成立.
成立.
(1)求此椭圆的离心率;
(2)设![]() 当点A在椭圆上运动时,求证
当点A在椭圆上运动时,求证![]() 始终是定值.
始终是定值.
17.解:(I)当![]() 时,
时,![]()
![]()
由椭圆定义,得![]()
在![]() 中,
中,![]()
![]()
(II)由![]() ,得
,得![]()
椭圆方程化为![]() ,即
,即![]()
焦点![]()
设![]()
(1)当直线AC的斜率存在时,直线AC的方程为![]()
代入椭圆方程,得![]()
![]() ,则
,则![]()
![]()
同理可得![]()
(2)当直线AC的斜率不存在时,![]()
综上所述,![]() 是定值6.
是定值6.
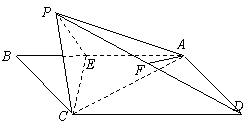 18.如图,在矩形ABCD中,AB=2BC,E为AB上一点,以直线EC为折线将点B折起至点P,并保持∠PEB为锐角,连结PA、PC、PD,取PD的中点F,若有AF∥平面PEC.
18.如图,在矩形ABCD中,AB=2BC,E为AB上一点,以直线EC为折线将点B折起至点P,并保持∠PEB为锐角,连结PA、PC、PD,取PD的中点F,若有AF∥平面PEC.
(Ⅰ)试确定点E的位置;
(Ⅱ)若异面直线PE、CD所成的角为60°,
求证:平面PEC⊥平面AECD.
18.(Ⅰ)点![]() 为
为![]() 的中点
的中点
证明如下:
取![]() 的中点
的中点![]() ,连
,连![]() .
.
由条件知![]() ,
,![]() .
.
则![]() 四点共面.
四点共面.
![]() 平面
平面![]() ,
,
平面![]() 平面
平面![]() ,
,![]() .
.
则四边形![]() 为平行四边形.
为平行四边形.
![]() .则
.则![]() 为
为![]() 的中点.
的中点.
(Ⅱ)![]() 所成的角为
所成的角为![]() ,∠PEB为锐角,
,∠PEB为锐角,
∴∠PEB=60°.
![]() ,∴△PEB为等边三角形.
,∴△PEB为等边三角形.
∴![]() .
.
作PH⊥平面![]() ,垂足为H,则HB = HE = HC.
,垂足为H,则HB = HE = HC.
∴H为△CBE的外心.
∵△CBE是直角三角形且∠B为直角,
∴外心H为斜边CE的中点.
∴H在CE上![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]() .
.
19.已知数列![]() 满足
满足![]() ,
,![]() .
.
(Ⅰ)求数列![]() 的通项公式
的通项公式![]() ;
;
(Ⅱ)设![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(Ⅲ)设![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() .求证:对任意的
.求证:对任意的![]() ,
,![]() .
.
19. 解:(Ⅰ)![]() ,
,![]() ,…3分
,…3分
又 ![]() ,
,
![]() 数列
数列 是首项为
是首项为![]() ,公比为
,公比为![]() 的等比数列.…5分
的等比数列.…5分
![]() , 即
, 即![]() . ………………6分
. ………………6分
(Ⅱ)![]() .
.
![]() .………9分
.………9分
(Ⅲ)![]() ,
,
![]() .
……………………10分
.
……………………10分
当![]() 时,则
时,则![]()
![]()
![]()
![]() .
.
![]() ,
, ![]() 对任意的
对任意的![]() ,
,![]() .
……………14分
.
……………14分
20.设关于x的方程![]() 有两个实根
有两个实根![]() 、
、![]() ,且
,且![]() .定义函数
.定义函数
![]()
(Ⅰ)求 ![]() 的值;
的值;
(Ⅱ)判断![]() 在区间
在区间![]() 上的单调性,并加以证明;
上的单调性,并加以证明;
(Ⅲ)若![]() 为正实数,证明不等式:
为正实数,证明不等式:![]()
20. 解:(Ⅰ)∵![]() 是方程
是方程![]() 的两个实根
的两个实根
∴![]()
∴![]()
同理![]()
∴![]() …………3分
…………3分
(Ⅱ)∵![]()
∴![]() …………4分
…………4分
当![]() 时,
时,![]() …………5分
…………5分
而![]()
∴![]() 在
在![]() 上为增函数
…………7分
上为增函数
…………7分
(Ⅲ)∵![]() 且
且![]()
∴![]()
![]()
∴![]() …………9分
…………9分
由(Ⅱ)可知![]()
同理可得![]() …………10分
…………10分
∴![]()
∴![]() …………12分
…………12分
又由(Ⅰ)知![]()
∴![]()
所以 ![]() …………14分
…………14分
21. 角铁是一种工业用钢料(如图),它成直二面角PQ-MN-RS(PQMN、RSMN是全等的长方形). 取MN的中点O,在QP上取点B、B1,在RS上取点A、A1,使 ![]() MOB=
MOB=![]() MOA=
MOA=![]() B1ON=
B1ON=![]() A1ON. 为给一物体棱的转角处包上角铁,可沿OA、OA1、OB、OB1切割出
A1ON. 为给一物体棱的转角处包上角铁,可沿OA、OA1、OB、OB1切割出![]() OAA1、
OAA1、![]() OBB1,然后将角铁绕内部折叠,将OA与OA1,OB与OB1焊合,并使
OBB1,然后将角铁绕内部折叠,将OA与OA1,OB与OB1焊合,并使![]() MON=
MON=![]() .
.
(1)设AB的中点为D,A1B1的中点为D1,证明焊接前M、D、D1、N四点共面;
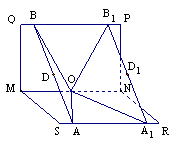 (2)求切割线OA与棱OM所成的角.
(2)求切割线OA与棱OM所成的角.
21. 简要答案:(1)方法一,证明DD1与MN平行
方法二过MN作一平面平分二面角,证D、D1在所 作平面内.
(2) ![]()