2007届福建莆田四中高三数学五月模拟(一)(文)
一.选择题(5×12=60)
1.若条件P:![]() ,条件Q:
,条件Q:![]() ,则P是Q的( )
,则P是Q的( )
A.充分不必要条 B.必要不充分条件 C.充要条件 D.既非充分条件也非必要条件
2、数列{an}满足a1=1, a2=![]() ,且
,且![]() (n≥2),则an等于(
)。
(n≥2),则an等于(
)。
(A)![]() (B)(
(B)(![]() )n-1 (C)(
)n-1 (C)(![]() )n (D)
)n (D)![]()
3. 把函数![]() 的图象适当变动,就可得到y=-sin3x的图象,这种变动可以是( )
的图象适当变动,就可得到y=-sin3x的图象,这种变动可以是( )
A 沿x轴向右平移![]() B 沿x轴向左平移
B 沿x轴向左平移![]()
C 沿x轴向右平移![]() D 沿x轴向左平移
D 沿x轴向左平移![]()
4.已知函数![]() 有极大值和极小值,则实数a的取值范围是( )
有极大值和极小值,则实数a的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5. 在![]() 中,
中,![]() ,则
,则![]() 的值为 ( )
的值为 ( )
A 20
B ![]() C
C ![]() D
D ![]()
6.设函数y=f(x)的图象关于直线x=1对称,在x≤1时,f(x)=(x+1)2-1,则x>1时f(x)等于( )
A![]() f(x)=(x+3)2-1 B
f(x)=(x+3)2-1 B![]() f(x)=(x-3)2-1
f(x)=(x-3)2-1
C![]() f(x)=(x-3)2+1 D
f(x)=(x-3)2+1 D![]() f(x)=(x-1)2-1
f(x)=(x-1)2-1
7. 在长方体相交于一个顶点的三条棱上各取一个点,那么过这三点的截面一定是( )。
A 三角形或四边形 B 锐角三角形
C 锐角三角形或钝角三角形 D.钝角三角形
8.现有同一型号的汽车50辆.为了了解这种汽车每耗油1 L所行路程的情况,要从中抽出5辆汽车在同一条件下进行砂油1 L所行路程的试验,得到如下数据(单位:![]() ):11,15,9,12,13
):11,15,9,12,13
则样本方差是( )
A.20 B.12 C.4 D.2
 |
9. 函数y=1-x-x2的图象大致是( )。
A B C D
10.过双曲线![]() 的一个焦点它的渐近线的垂线,垂足为M,延长FM交y轴于E,若M为EF的中点,则该双曲线的离心率为 ( )
的一个焦点它的渐近线的垂线,垂足为M,延长FM交y轴于E,若M为EF的中点,则该双曲线的离心率为 ( )
A.2 B.![]() C.3 D.
C.3 D.![]()
11. 已知实数x,y满足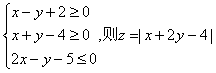 的最大值为: ( )
的最大值为: ( )
A.19 B.20 C.21 D.18
12.五一将至,小张制定了一项三日游计划,从莆田的七个景点中选择5个进行游览。如果湄洲妈祖、九鲤湖为必选景点,并且在游览过程中必须按先湄洲妈祖后九鲤湖的次序经过两景点,则不同的游览线路有( )
A.120种 B.240种 C.480种 D.600种
二.填空题(4×4=16)
13.![]() 的展开式中的常数项是________.
的展开式中的常数项是________.
14. 设甲、已、丙三人每次射击命中目标的概率分别为0.7、0.6和0.5.
三人各向目标射击一次,则至少有一人命中目标的概率是 ;若甲单独向目标射击三次,他恰好命中两次的概率是 .
15.有这样一首诗:“有个学生资性好,一部《孟子》三日了,每日添增一倍多,问君每日读多少?”(注:《孟子》全书共34685字,“一倍多”指一倍),由此诗知该君第二日读的字数为 .
16.已知定义在R上的函数![]() 是以2为周期的奇函数,则方程
是以2为周期的奇函数,则方程![]() 在区间[-2,2]上至少有 个实数根.
在区间[-2,2]上至少有 个实数根.
三.解答题.(12+12+12+12+12+14=74)
17.在△ABC中,AB=AC,且![]() ,
,
(Ⅰ)求![]() 的值;(II)求
的值;(II)求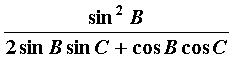 的值.
的值.
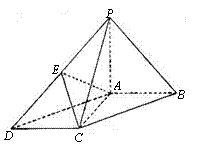
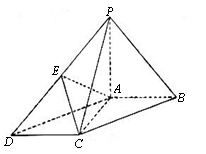 18.如图,在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥平面ABCD,且PA=AB,点
18.如图,在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥平面ABCD,且PA=AB,点![]() 是PD中点.
是PD中点.
(Ⅰ)求证:AC⊥PB;
(Ⅱ)求证: PB∥平面AEC;
(Ⅲ)求二面角E-AC-B的大小.
19. 设数列![]() 的前
的前![]() 项和为
项和为![]() ,
,![]() ,
,![]() .
.
⑴求证:![]() 是等差数列.
是等差数列.
⑵设![]() 是数列
是数列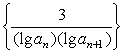 的前
的前![]() 项和,求使
项和,求使![]()
对所有的![]() 都成立的最大正整数
都成立的最大正整数![]() 的值.
的值.
20. 市政府为招商引资,决定对外资企业第一年产品免税.某外资厂该年A型产品出厂价为每件60元,年销售量为11.8万件.第二年,当地政府开始对该商品征收税率为p%(0<p<100,即销售100元要征收p元)的税收,于是该产品的出厂价上升为每件![]() 元,预计年销售量将减少p万件.
元,预计年销售量将减少p万件.
(Ⅰ)将第二年政府对该商品征收的税收y(万元)表示成p的函数,并指出这个函数的定义域;
(Ⅱ)要使第二年该厂的税收不少于16万元,则税率p%的范围是多少?
21.已知函数f(x)=x3-ax2-(3+2a)x+b (x∈R)
(1)试求函数f(x)递增区间;
(2)若函数f(x)在[-1,1]上有两个不同的极值点,试求a的取值范围.
|
(I)求椭圆的方程;
(II)过点P(0,3)引直线l顺次交椭圆于
|
2007届莆田四中高三数学五月模拟(一)(文)(答案)
BADCB BBCCD CD 13.15 14 0.94 , 0.441 15.9910 16.5
17.解:(I)由题意知:![]() ,则
,则![]() ,
,
而![]() ,则
,则![]() .
.
(II)![]()
![]()
![]()
 18. 解:(1)由PA⊥平面ABCD可得PA^AC又AB⊥AC,所以AC^平面PAB,所以AC⊥PB
18. 解:(1)由PA⊥平面ABCD可得PA^AC又AB⊥AC,所以AC^平面PAB,所以AC⊥PB
(2)如图,连BD交AC于点O,连EO,则
EO是△PDB的中位线,\EO∥PB
\PB∥平面AEC
(3)如图,取AD的中点F,连EF,FO,则EF是△PAD的中位线,\EF∥PA又PA⊥平面ABCD,\EF^平面ABCD
同理FO是△ADC的中位线,\FO∥AB\FO^AC由三垂线定理可知\ÐEOF是二面角E-AC-D的平面角.又FO=![]() AB=
AB=![]() PA=EF\ÐEOF=45°而二面角E-AC-B与二面角E-AC-D互补,故所求二面角E-AC-B的大小为135°.
PA=EF\ÐEOF=45°而二面角E-AC-B与二面角E-AC-D互补,故所求二面角E-AC-B的大小为135°.
19解:⑴依题意,![]() ,故
,故![]() ,
,
当![]() 时,
时,![]() ① 又
① 又![]() ②
②
②―①整理得:![]() ,故
,故![]()
![]() 为等比数列, 且
为等比数列, 且![]() ,
,![]()
![]() ,即
,即![]() 是等差数列.
是等差数列.
⑵由⑴知,![]()
=![]()
![]() ,依题意有
,依题意有![]() ,解得
,解得![]() ,故所求最大正整数
,故所求最大正整数![]() 的值为
的值为![]() .
.
20.(I)解:依题意,第二年该商品年销售量为(11.8-p)万件,
年销售收入为![]() (11.8-p)万元,
(11.8-p)万元,
政府对该商品征收的税收y=![]() (11.8-p)p%(万元)
(11.8-p)p%(万元)
故所求函数为y=![]() (11.8-p)p分
(11.8-p)p分
由11.8-p>0及p>0得定义域为0<p<11.8
(II)解:由y≥16得![]() (11.8-p)p≥16
(11.8-p)p≥16
化简得p2-12p+20≤0,即(p-2)(p-10) ≤0,解得2≤p≤10. 故当税率在[0.02,0.1]内时,税收不少于16万元.……………………8分
21.解: (1)f(x)=3x2-2ax-(3+2a)=(x+1)[3x-(3+2a)] 令f(x)=0得,x=-1或x=![]()
若a<-3,则当x<![]() 时,f(x)>0;当
时,f(x)>0;当![]() <x<-1时,f(x)<0;
<x<-1时,f(x)<0;
当a=-3,则![]() =-1,此时f(x)≥0恒成立,所以所求递增区间是(-∞,+∞)
=-1,此时f(x)≥0恒成立,所以所求递增区间是(-∞,+∞)
若a>-3,则当x<-1时,f(x)>0,f(x)>0;当-1<x<![]() 时,f(x)<0;当x>
时,f(x)<0;当x>![]() 时 f(x)>0,的以a>-3时,所求递增区间是(-∞,-1)和(
时 f(x)>0,的以a>-3时,所求递增区间是(-∞,-1)和(![]() ,+∞)
,+∞)
(2)f(x)在[-1,1]上有两个不同的极值点 ∴f(x)=0在[-1,1]上有两个不同的实数解,即方程3x2-2ax-(3+2a)=0在[-1,1]上有两个不同的实数解.
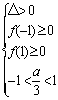 解得:-3<a≤0
解得:-3<a≤0
22解:(Ⅰ)∵椭圆的右焦点为F(![]() ,0)
,0) ![]()
又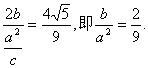 ………………(3分)
………………(3分)
又![]()
所以,椭圆的方程为![]() ………………(7分)
………………(7分)
(Ⅱ)若直线![]() 轴重合,此时
轴重合,此时![]() .………………(9分)
.………………(9分)
若直线l与y轴不重合,设直线l的方程![]() ,代入椭圆方程为
,代入椭圆方程为![]() 消去y得
消去y得
![]()
设![]()
![]()
所以,![]() ①
①
![]() ②
②
①、②两式消去x2得
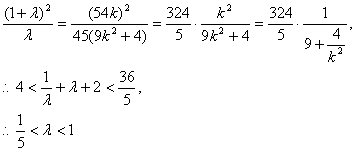 综上,
综上,![]()