2007届福建莆田四中高三数学五月模拟(一)(理)
一.选择题(5×12=60)
1.若条件P:![]() ,条件Q:
,条件Q:![]() ,则P是Q的( )
,则P是Q的( )
A.充分不必要条 B.必要不充分条件 C.充要条件 D.既非充分条件也非必要条件
2、数列{an}满足a1=1, a2=![]() ,且
,且![]() (n≥2),则an等于(
)。
(n≥2),则an等于(
)。
(A)![]() (B)(
(B)(![]() )n-1 (C)(
)n-1 (C)(![]() )n (D)
)n (D)![]()
3. 把函数![]() 的图象适当变动,就可得到y=-sin3x的图象,这种变动可以是( )
的图象适当变动,就可得到y=-sin3x的图象,这种变动可以是( )
A 沿x轴向右平移![]() B 沿x轴向左平移
B 沿x轴向左平移![]()
C 沿x轴向右平移![]() D 沿x轴向左平移
D 沿x轴向左平移![]()
4.已知函数![]() 有极大值和极小值,则实数a的取值范围是( )
有极大值和极小值,则实数a的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5. 在![]() 中,
中,![]() ,则
,则![]() 的值为 ( )
的值为 ( )
A 20
B ![]() C
C ![]() D
D ![]()
6.设函数y=f(x)的图象关于直线x=1对称,在x≤1时,f(x)=(x+1)2-1,则x>1时f(x)等于( )
A![]() f(x)=(x+3)2-1 B
f(x)=(x+3)2-1 B![]() f(x)=(x-3)2-1
f(x)=(x-3)2-1
C![]() f(x)=(x-3)2+1 D
f(x)=(x-3)2+1 D![]() f(x)=(x-1)2-1
f(x)=(x-1)2-1
7. 在长方体相交于一个顶点的三条棱上各取一个点,那么过这三点的截面一定是( )。
 A
三角形或四边形
B 锐角三角形
A
三角形或四边形
B 锐角三角形
C 锐角三角形或钝角三角形 D.钝角三角形
8.某路段检查站监控录象显示,在某时段内,
有1000辆汽车通过该站,现在随机抽取其中的
200辆汽车进行车速分析,分析的结果表示为
如右图的频率分布直方图,则估计在这一时段内
通过该站的汽车中速度不小于90km/h 的约有( )
A.100辆 B.200辆 C.300辆 D.400辆
 |
9. 函数y=1-x-x2的图象大致是( )。
A B C D
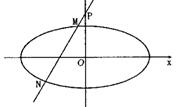
10.过双曲线![]() 的一个焦点F引它的渐近线的垂线,垂足为M,延长FM交y轴于E,若M为EF的中点,则该双曲线的离心率为 ( )
的一个焦点F引它的渐近线的垂线,垂足为M,延长FM交y轴于E,若M为EF的中点,则该双曲线的离心率为 ( )
A.2 B.![]() C.3 D.
C.3 D.![]()
11. 若方程x2+(1+a)x+1+a+b=0的两根分别为椭圆,双曲线的离心率,
则![]() 的取值范围是( )
的取值范围是( )
A.-2<![]() <-1 B.
<-1 B.![]() <-2或
<-2或![]() >-1 C.-2<
>-1 C.-2<![]() <-
<-![]() D.
D.![]() >-
>-![]() 或
或![]() <-2
<-2
12.若m.n均为非负整数,在做m+n的加法时各位均不进位(例如,134+3802=3936),则称(m,n)为“简单的”有序对,而m+n称为有序数对(m,n)的值,那么值为1942的“简单的”有序对的个数是 ( )
A、20 B、16 C、150 D、300
二.填空题(4×4=16)
13.![]() 的展开式中的常数项是________.
的展开式中的常数项是________.
14.设z满足z+![]() =2+i,那么z等于
.
=2+i,那么z等于
.
15.有这样一首诗:“有个学生资性好,一部《孟子》三日了,每日添增一倍多,问君每日读多少?”(注:《孟子》全书共34685字,“一倍多”指一倍),由此诗知该君第二日读的字数为 .
16.若定义在R上的函数![]() 的反函数是
的反函数是![]() ,且
,且![]() ,则
,则![]() .
.
三.解答题.(12+12+12+12+12+14=74)
17.在![]() 中,
中,![]() 的对边分别为
的对边分别为![]() 且
且![]() 成等差数列.
成等差数列.
(I)求B的值;(II)求![]() 的范围。
的范围。
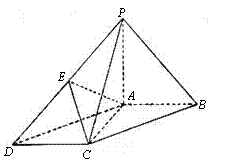 18.如图,在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥平面ABCD,且PA=AB,点
18.如图,在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥平面ABCD,且PA=AB,点![]() 是PD中点.
是PD中点.
(Ⅰ)求证:AC⊥PB;
(Ⅱ)求证: PB∥平面AEC;
(Ⅲ)求二面角E-AC-B的大小.
19.已知函数f(x)的图像与函数![]() 的图像关于点A(0,1)对称.
的图像关于点A(0,1)对称.
(1)求f(x)的解析式;
(2)若![]() ,且
,且![]() 在区间(0,
在区间(0,![]() 上为减函数,求实数a的取值范围.
上为减函数,求实数a的取值范围.
20.据某地气象部门统计,该地区每年最低气温在![]() 以下的概率为
以下的概率为![]()
(1)设![]() 为该地区从2005年到2010年最低气温在
为该地区从2005年到2010年最低气温在![]() 以下的年数,求
以下的年数,求![]() 的分布列。
的分布列。
(2)设![]() 为该地区从2005年到2010年首次遇到最低气温在
为该地区从2005年到2010年首次遇到最低气温在![]() 以下经过的年数,求
以下经过的年数,求![]() 的分布列。(以上两小题只列式不计算)
的分布列。(以上两小题只列式不计算)
|
(I)求椭圆的方程;
(II)过点P(0,3)引直线l顺次交椭圆于
|
22.已知![]() 为锐角,且
为锐角,且![]() ,函数
,函数![]() ,数列{an}的首项
,数列{an}的首项![]() .
.
⑴ 求函数![]() 的表达式;
的表达式;
⑵ 求证:![]() ;
;
⑶ 求证: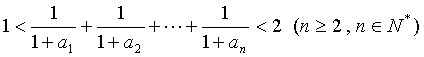
2007届莆田四中高三数学五月模拟(一)(理)(答案)
BADCB BBCCD CD 13. 15 14. ![]() 15. 9910 16.2007
15. 9910 16.2007
17、解:![]()
![]() 成等差数列,
成等差数列,
![]()
![]()
由正弦定理得,![]()
代入得,![]()
即:![]()
![]()
![]()
又在![]() 中,
中,![]() ,
,![]()
![]()
![]()
![]() ,
,![]()
![]() .
.
(II)![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]() 的范围是
的范围是![]()
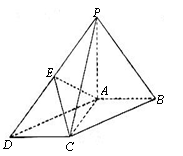 18. 解:(1)由PA⊥平面ABCD可得PA^AC又AB⊥AC,所以AC^平面PAB,所以AC⊥PB
18. 解:(1)由PA⊥平面ABCD可得PA^AC又AB⊥AC,所以AC^平面PAB,所以AC⊥PB
(2)如图,连BD交AC于点O,连EO,则EO是△PDB的中位线,\EO∥PB\PB∥平面AEC
(3)如图,取AD的中点F,连EF,FO,则EF是△PAD的中位线,\EF∥PA又PA⊥平面ABCD,\EF^平面ABCD
同理FO是△ADC的中位线,\FO∥AB\FO^AC由三垂线定理可知\ÐEOF是二面角E-AC-D的平面角.又FO=![]() AB=
AB=![]() PA=EF\ÐEOF=45°而二面角E-AC-B与二面角E-AC-D互补,故所求二面角E-AC-B的大小为135°.
PA=EF\ÐEOF=45°而二面角E-AC-B与二面角E-AC-D互补,故所求二面角E-AC-B的大小为135°.
19.解析:(1)设f(x)图像上任一点坐标为(x,y),点(x,y)关于点A(0,1)的对称点(-x,2-y)在h(x)图像上
∴ ![]() , ∴
, ∴ ![]() ,即
,即 ![]()
(2)![]() , ∵
, ∵ ![]()
![]() 在(0,
在(0,![]() 上递减,∴
上递减,∴ ![]() 在
在![]() (0,
(0,![]() 时恒成立.
时恒成立.
即 ![]() 在
在![]() (0,
(0,![]() 时恒成立. ∵
时恒成立. ∵ ![]() (0,
(0,![]() 时,
时,![]() ∴
∴![]() .
.
20.(1)将每年的气温情况看做一次试验,则遇到最低气温在![]() 以下的概率为
以下的概率为![]() ,且每次实验结果是相互独立的。
,且每次实验结果是相互独立的。
故![]() ,以此为基础求
,以此为基础求![]() 的分布列
的分布列
所以![]() 的分布列为
的分布列为![]()
(2)由于![]() 表示该地区从2005年到2010年首次遇到最低气温在
表示该地区从2005年到2010年首次遇到最低气温在![]() 以下经过的年数,显然
以下经过的年数,显然![]() 是随机变量,其取值为0,1,2,3,4,5,
是随机变量,其取值为0,1,2,3,4,5,
其中![]() 表示前
表示前![]() 年没有遇到最低气温在
年没有遇到最低气温在![]() 以下的情况,但在第
以下的情况,但在第![]() 年遇到了最低气温在
年遇到了最低气温在![]() 以下的情况,故各概率应按独立事件同时发生计算。
以下的情况,故各概率应按独立事件同时发生计算。![]()
而![]() 表示这6年没有遇到最低气温在
表示这6年没有遇到最低气温在![]() 以下的情况,
以下的情况,
故其概率为![]() ,因此
,因此![]() 的分布列为:
的分布列为:
|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|
|
|
|
|
|
|
|
|
21.解:(Ⅰ)∵椭圆的右焦点为F(![]() ,0)
,0) ![]()
又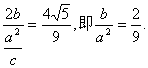 又
又![]()
所以,椭圆的方程为![]()
(Ⅱ)若直线![]() 轴重合,此时
轴重合,此时![]() .
.
若直线l与y轴不重合,设直线l的方程![]() ,代入椭圆方程为
,代入椭圆方程为![]() 消去y得
消去y得
![]()
设![]()
![]()
所以,![]() ①
①
![]() ② ①、②两式消去x2得
② ①、②两式消去x2得
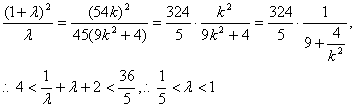 综上,
综上,![]()
22.解:⑴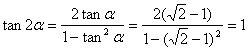 又∵
又∵![]() 为锐角
为锐角
∴![]() ∴
∴![]()
![]()
⑵ ![]() ∵
∵![]() ∴
∴![]() 都大于0
都大于0
∴![]() ∴
∴![]()
⑶ ![]()
∴![]()
∴![]()
![]()
∵![]() ,
, ![]() , 又∵
, 又∵![]()
∴![]() ∴
∴![]()
∴![]()