2008届高三数学强化训练卷1与答案
高 班 姓名 得分
一 
选择题：
1．函数
的奇偶性和周期是（ ）
A．奇函数，周期是 
B．奇函数，周期是
C．非奇非偶函数，周期是 D．非奇非偶函数，周期是
2．函数
的大致图形为 （ ）
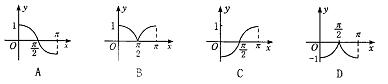
3．已知sin(
＋
)＝
，sin(－)＝
，则
的值为（ ）
A． 5 B．
C． D．2
4．函数
的值域是（ ）A．
B．
C．
D．
5．今有一组生物实验数据如下：
| x | 0 | 0.2616 | 0.4361 | 0.7854 | 1.3089 |
| y | 0 | 0.2588 | 0.4226 | 0.7085 | 0.9125 |
现准备用下列函数中的某个函数近似表示数据满足的规律，其中接近的一个是( )
A．y=tanx B．y=1-cosx C．y=sinx D．y=
6.使函数
为奇函数，且在[O，
]上是减函数的
的一个值是（ ）
A．
B．
C．
D．
7．已知
，则函数
的最大值和最小值分别是（ ）
A．
B．2，0 C．
D．
8．若将函数
（
均为常数，
）针对所作的
图象变换(振幅变换、周期变换、相位变换)权且暂用表示的话，下面两图中所演示的图象变换
顺序则可能有以下几种：①
； ②
； ③
； ④
； ⑤
； ⑥
．
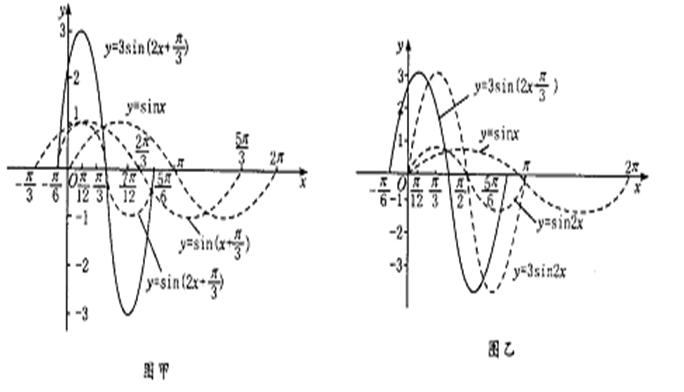
请问：经过比较，你认为图甲、图乙最合适的变换顺序分别是（ ）
A．⑥、⑤ B．⑥、③ C．⑤、⑥ D．以上都不对
9．若三角形的两内角，满足tantan<1，则这个三角形的形状是（ ）
A．锐角三角形 B．钝角三角形 C．直角三角形 D．不能确定
10．对于函数
，
①该函数是以为最小正周期的周期函数；②该函数的值域是[-1,1]；③当且仅当
时，
；④当且仅当
时，该函数取得最大值1；⑤该函数在区间[
，
]上单调递增． 以上五个命题中正确命题的个数是（ ）
A．1 B． 2 C．3 D．4
二、填空题：
11.若
是偶函数，则a= .
12．把函数
的图象向右平移
个单位，再把所得图象上各点的横坐标缩短
为原来的（纵坐标不变），则所得图象的解析式为
.
13．
的值是
14．已知函数
的最小正周期为3，则A= 
15．函数
在区间[
]的最小值为______
三、解答题：
16．（本小题满分12分）已知
的值.
17．已知
的值
18. 若
，
,
，求
的值；
19．（北京卷）已知函数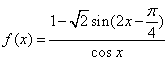
，
（Ⅰ）求
的定义域；
（Ⅱ）设是第四象限的角，且
，求
的值.
20.已知函数f(x)=A
(A>0,
>0,0<<
函数，且y=f(x)的最大值为2，其图象相邻两对称轴间的距离为2，并过点（1，2）.
（1）求;
（2）计算f(1)+f(2)+… +f(2 008).
21. 已知函数f(x)=sin(2x－)+2sin2(x－) (x∈R)
(Ⅰ)求函数f(x)的最小正周期 ; (2)求使函数f(x)取得最大值的x的集合.
2008届高三数学强化训练卷1（三角函数1）答案
一、 1、B；2、B； 3、 A； 4、 B； 5、 C； 6、B；7、A; 8、D; 9、B; 10、A.
二、11． （湖南卷）若是偶函数，则a= .
解析：
是偶函数，取a=－3，可得
为偶函数。
12． 
；13、4； 14、
；15、1；
三、
16．
……5分
由
两边平方得
…9分
而
，故原式
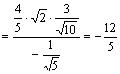……12分
湖北卷文理17．已知的值
解：由已知得：
由已知条件可知
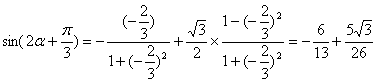
18.(重庆卷)若，,，则的值
解：由
，则
，
，又
，
，所以
，
解得
，所以 ＝
.
19．（北京卷）已知函数，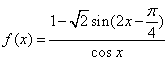
（Ⅰ）求的定义域；
（Ⅱ）设是第四象限的角，且，求的值.
解：（1）依题意，有cosx¹0，解得x¹kp＋，
即的定义域为｛xxÎR，且x¹kp＋，kÎZ｝
（2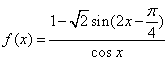）＝－2sinx＋2cosx\＝－2sina＋2cosa
由是第四象限的角，且可得sina＝－
，cosa＝
\＝－2sina＋2cosa＝
20.（2006山东卷）已知函数f(x)=A(A>0,>0,0<<函数，且y=f(x)的最大值为2，其图象相邻两对称轴间的距离为2，并过点（1，2）.
（1）求;
（2）计算f(1)+f(2)+… +f(2 008).
解：（I）
的最大值为2，
.
又
其图象相邻两对称轴间的距离为2，
，
.
过
点，
又
.
（II）解法一：
，
.
又的周期为4，
，
解法二：
又
的周期为4，，
21.(2006陕西卷)已知函数f(x)=sin(2x－)+2sin2(x－) (x∈R)
(Ⅰ)求函数f(x)的最小正周期 ; (2)求使函数f(x)取得最大值的x的集合.
解:(Ⅰ) f(x)=sin(2x－)+1－cos2(x－)
= 2[sin2(x－)－ cos2(x－)]+1
=2sin[2(x－)－]+1
= 2sin(2x－) +1
∴ T==π
(Ⅱ)当f(x)取最大值时， sin(2x－)=1，有 2x－ =2kπ+
即x=kπ+ (k∈Z) ∴所求x的集合为{x∈Rx= kπ+ ， (k∈Z)}．