绝密★启用前 试卷类型:A
广东省深圳市2007年高三年级第二次调研考试
数学(理科)
2007.5
本试卷分选择题和非选择题(含选做题)两部分,共6页,满分150分。考试用时120分钟。
注意事项:
1. 答卷前,考生首先检查答题卡是否整洁无缺损,监考教师分发的重重信息条形码是否正确;之后务必用0.5毫米黑色字迹的签字笔在答题卡指定位置填写自己的学校、姓名和考生号,同时,将监考教师发放的条形码正向准确粘贴在答题卡的贴条形码区,请保持条形码整洁、不污损。
2. 选择题每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案,答案不能答在试卷上。不按要求填涂的,答案无效。
3. 百选择题必须用0.5毫米黑色字迹的签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上,请注意每题答题空间,预先合理安排;如需改动先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液。不按以上要求作答的答案无效。
4. 考生必须保持答题卡的整洁,考试结束后,答题卡与试卷一并交回。
参考公式:
如果说事件A、B互斥,那么![]() ;
;
如果C为椭圆![]() 的半焦距,则该椭圆的准线方程为
的半焦距,则该椭圆的准线方程为![]() .
.
第一部分 选择题(共40分)
一、选择题:本大题共8小题,每小题5分,共4分.在每小题给出的四个选项中,有且只有一项是符合题目要求的。
1.已知集合![]()
A 2 B 3 C 4 D 8
2.已知![]()
A 4
B —4
C ![]() D
D ![]()
3.设![]() ,
,![]() ,
,![]() ,则
,则![]()
![]()
![]() 的大小顺序是
的大小顺序是
A ![]() B
B![]() C
C ![]() D
D ![]()
4.在△ABC中,![]()
![]()
![]() 分别是∠A、∠B、∠C的对边,且
分别是∠A、∠B、∠C的对边,且![]() ,则∠A等于
,则∠A等于
A 60° B 30° C 120° D 150°
5.已知命题![]() :
:![]() ,命题
,命题![]() :
: ![]() 。若命题
。若命题![]() 是真命题,则实数
是真命题,则实数![]() 的取值范围为
的取值范围为
A
![]() B
B ![]()
C ![]() D
D ![]()
6.已知![]() ,A是由直线
,A是由直线![]() 围成的曲边三角形的平面区域,若向区域
围成的曲边三角形的平面区域,若向区域![]() 上随机投一点P,则P落在区域A内的概率为
上随机投一点P,则P落在区域A内的概率为
A ![]() 了 B
了 B![]() C
C ![]() D
D ![]()
7.在教材中,我们学过“经过点![]() 的平面的方程是:
的平面的方程是:![]() ”。现在我们给出平面
”。现在我们给出平面![]() 的方程是
的方程是![]() ,平面
,平面![]() 的方程是
的方程是![]() ,则由这两平面所成的锐二面角的余弦值是
,则由这两平面所成的锐二面角的余弦值是
A ![]() B
B![]() C
C ![]() D
D![]()
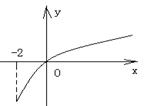 8.已知函数
8.已知函数![]() 的定义域为[—2,
的定义域为[—2,![]() ,部分对应值如下表。
,部分对应值如下表。![]() 为
为![]() 的导函数,函数
的导函数,函数![]() 的图象如下图所示。
的图象如下图所示。
|
| —2 | 0 | 4 |
|
| 1 | —1 | 1 |
若两正数![]() 的取值范围是
的取值范围是
A
![]() B
B ![]() C
C ![]() D
D ![]()
第二部分 非选择题(共100分)
二、填空题:本大题共7小题,分必做题和选做题,每小题5分,共30分,必做题:第9、10、11、12题为必做题。
9.已知数列{![]() }是公差不为0的等差数列,
}是公差不为0的等差数列,![]() 为数列{
为数列{![]() }的前
}的前![]() 项和,
项和,![]() ______________.
______________.
10.设二项式![]() 展开式各项的系数和为P,二项式系数之和为S,P+S=72,则正整数
展开式各项的系数和为P,二项式系数之和为S,P+S=72,则正整数![]() ,展开式中常数项的值为
。
,展开式中常数项的值为
。
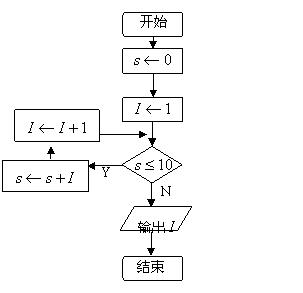
11.阅读下面的程序框图,输出的结果为
|

12.已知抛物线![]() 与直线
与直线![]() 交于A、B两点,如果在该抛物线上存在点C,使得
交于A、B两点,如果在该抛物线上存在点C,使得![]() 。
。
▲  选做题:从第13、14、15三道题中选做两题,三题都答的只计算前两题的得分。
选做题:从第13、14、15三道题中选做两题,三题都答的只计算前两题的得分。
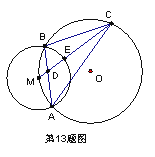
13.如图,⊙![]() 和⊙
和⊙![]() 交于A、B两点,点
交于A、B两点,点![]() 在⊙
在⊙![]() 上,⊙
上,⊙![]() 的弦
的弦![]() 分别与弦AB、⊙
分别与弦AB、⊙![]() 交于D、E两点,若
交于D、E两点,若![]() 则⊙
则⊙![]() 的半径为
。
的半径为
。
14.若直线![]() 有两个不同的交点,则实数
有两个不同的交点,则实数![]() 的取值范围是
。
的取值范围是
。
15.关于![]() 的不等式
的不等式![]() 则实数
则实数![]() 的最大值是
。
的最大值是
。
三、解答题:本大题6个小题,共80分,解答应写出文字说明,证明过程或演算步骤。
16.(本小题满分12分)
已知![]() ,设
,设![]() 。
。
(Ⅰ)求函数![]() 的最小正周期;
的最小正周期;
(Ⅱ)当![]() 时,求函数
时,求函数![]() 的最大值及最小值。
的最大值及最小值。
17.(本小题满分12分)
有编号为![]() 个学生,入坐编号为
个学生,入坐编号为![]() 个座位。每个学生规定坐一个座位,设学生所坐的座位号与该生的编号不同的学生人数为
个座位。每个学生规定坐一个座位,设学生所坐的座位号与该生的编号不同的学生人数为![]() ,已知
,已知![]() 时,共有6种坐法。
时,共有6种坐法。
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)求随机变量![]() 的概率分布列和数学期望。
的概率分布列和数学期望。
18.(本小题满分14分)
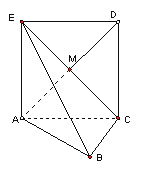
如图,正方形![]() 所在的平面与平面
所在的平面与平面![]() 垂直,
垂直,![]() 是
是![]() 的交点,
的交点,![]() ,且
,且![]() 。
。
(Ⅰ)求证:![]() ;
;
(Ⅱ)求直线AB与平面![]() 所成角的大小;
所成角的大小;
(Ⅲ)求二面角![]() 的大小不。
的大小不。
19.(本小题满分14分)
设![]() 是定义在[—1,1]上的奇函数,且当
是定义在[—1,1]上的奇函数,且当![]() 时,
时,![]()
![]()
(Ⅰ)若函数![]() 的解析式;
的解析式;
(Ⅱ)当![]() 时,求函数
时,求函数![]() 在(0,1]上的最大值
在(0,1]上的最大值![]() ;
;
(Ⅲ)如果对满足![]() 的一切实数
的一切实数![]() ,函数
,函数![]() 在(0,1]上恒有
在(0,1]上恒有![]() ,求实数
,求实数![]() 的取值范围。
的取值范围。
20.(本小题满分14分)
已知椭圆C的中心为原点,点F(1,0)是它的一个焦点,直线![]() 过点F与椭圆C交于点A、B两点,且当直线
过点F与椭圆C交于点A、B两点,且当直线![]() 垂直于
垂直于![]() 轴时,
轴时, ![]() 。
。
(Ⅰ)求椭圆C的方程;
(Ⅱ)是否存在直线![]() ,使得在椭圆C的右准线上可以找到一点P,满足
,使得在椭圆C的右准线上可以找到一点P,满足![]() 为正三角形。如果存在,求出直线
为正三角形。如果存在,求出直线![]() 的方程;如果不存在,请说明理由。
的方程;如果不存在,请说明理由。
21.(本小题满分14分)
已知数列![]() 满足
满足![]() 。
。
(Ⅰ)试判断数列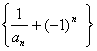 是否为等比数列,并说明理由;
是否为等比数列,并说明理由;
(Ⅱ)设![]() ,求数列
,求数列![]() 的前
的前![]() ;
;
(Ⅲ)设![]() ,数列
,数列![]() 的前
的前![]() 。求证:对任意的
。求证:对任意的![]()
![]() 。
。
广东省深圳市2007年高三年级第二次调研考试
数学(理科)答案及评分标准
说明:
一、本解答给出了一种或几种解法供参考,如果考生的解法与本解答不同,可根据试题的主要考查内容比照评分标准制订相应的评分细则.
二、对计算题当考生的解答在某一步出现错误时,如果后续部分的解答未改变该题的内容和难度,可视影响的程度决定给分,但不得超过该部分正确解答应得分数的一半;如果后续部分的解答有较严重的错误,就不再给分.
三、解答右端所注分数,表示考生正确做到这一步应得的累加分数.
四、只给整数分数,选择题和填空题不给中间分数.
一、选择题:本大题每小题5分,满分40分.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| C | B | C | D | A | D | A | B |
二、填空题:第9、10、11、12题为必做题,第13、14、15题为选做题,三题都答的只计算前两题的得分.每小题5分(第10题前空2分,后空3分),满分30分.
9.![]() .
10.
.
10.![]() ,
,![]() .
11.
.
11.![]() .
12.
.
12.![]() .
.
13.![]() .
14.
.
14.![]() . 15.
. 15.![]() .
.
三.解答题:本大题6小题,共80分.解答应写出文字说明,证明过程或演算步骤.
16.(本小题满分12分)已知![]() ,设
,设![]() .
.
(Ⅰ)求函数![]() 的最小正周期;
的最小正周期;
(Ⅱ)当![]() ,
,![]() 时,求函数
时,求函数![]() 的最大值及最小值.
的最大值及最小值.
解:(Ⅰ)![]()
![]() =
= ![]() ……2分
……2分
= ![]() =
= ![]() …………………3分
…………………3分
= ![]() =
=![]() . ………………5分
. ………………5分
∴![]() 的最小正周期
的最小正周期![]() .
………………………………6分
.
………………………………6分
(Ⅱ)∵ ![]()
![]() , ∴
, ∴![]() .
.
∴当![]() ,即
,即![]() =
=![]() 时,
时,![]() 有最大值
有最大值![]() ;
………………10分
;
………………10分
当![]() ,即
,即![]() =
=![]() 时,
时,![]() 有最小值
有最小值![]() .
……………12分
.
……………12分
17.(本小题满分12分)有编号为![]() 的
的![]() 个学生,入坐编号为
个学生,入坐编号为![]() 的
的![]() 个座位.每个学生规定坐一个座位,设学生所坐的座位号与该生的编号不同的学生人数为
个座位.每个学生规定坐一个座位,设学生所坐的座位号与该生的编号不同的学生人数为![]() ,已知
,已知![]() 时,共有
时,共有![]() 种坐法.
种坐法.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)求随机变量![]() 的概率分布列和数学期望.
的概率分布列和数学期望.
解:(Ⅰ)![]() 当
当![]() 时,有
时,有![]() 种坐法,
……………………………2分
种坐法,
……………………………2分
![]() ,即
,即![]() ,
,
![]() ,
,![]() 或
或![]() (舍去).
(舍去).
![]() .
………………………………4分
.
………………………………4分
(Ⅱ)![]() 的可能取值是
的可能取值是![]() ,
,
又![]()
![]() ,
, ![]() ,
,
![]() ,
,![]() , ………………………………8分
, ………………………………8分
![]() 的概率分布列为:
的概率分布列为:
|
|
|
|
|
|
| P |
|
|
|
|
……………………10分
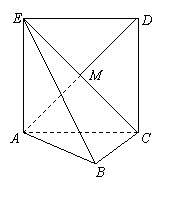 则
则![]() .
……………………12分
.
……………………12分
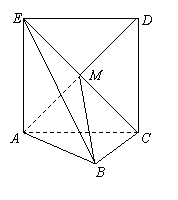
18.(本小题满分14分)
如图,正方形![]() 所在的平面与平面
所在的平面与平面![]() 垂直,
垂直,
![]() 是
是![]() 和
和![]() 的交点,
的交点,![]() ,且
,且![]() .
.
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求直线![]() 与平面
与平面![]() 所成的角的大小;
所成的角的大小;
(Ⅲ)求二面角![]() 的大小.
的大小.
解法一:(Ⅰ)∵四边形![]() 是正方形,
是正方形,
![]() . ………………………1分
. ………………………1分
∵平面![]() 平面
平面![]() ,
,
又∵![]() ,
,
![]() 平面
平面![]() .……………………3分
.……………………3分
![]() 平面
平面![]() ,
,
![]()
![]() . …………………………4分
. …………………………4分
![]() 平面
平面![]() . ………………5分
. ………………5分
(Ⅱ)连结![]() ,
,
![]() 平面
平面![]() ,
,
![]() 是直线
是直线![]() 与平面
与平面![]() 所成的角.
……………………………5分
所成的角.
……………………………5分
设![]() ,则
,则
![]() ,
,![]() ,
……………………………………………6分
,
……………………………………………6分
![]() ,
,
![]() .
.
即直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() . ……………………………………………8分
. ……………………………………………8分
(Ⅲ)过![]() 作
作![]() 于
于![]() ,连结
,连结![]() . ……………………………………………9分
. ……………………………………………9分
![]() 平面
平面![]() ,
,
![]() .
.
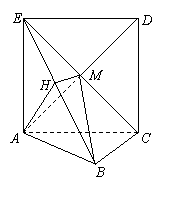
![]() 平面
平面![]() .
.
![]() 是二面角
是二面角![]() 的平面角. ……10分
的平面角. ……10分
∵平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() .
.
![]()
![]() .
.
在![]() 中,
中, ![]() ,有
,有![]() .
.
由(Ⅱ)所设![]() 可得
可得
![]() ,
,![]() ,
,
![]() .
……………………………………………12分
.
……………………………………………12分
![]() .
.
![]() .
.
∴二面角![]() 等于
等于![]() .
……………………………………………14分
.
……………………………………………14分
解法二: ∵四边形![]() 是正方形 ,
是正方形 ,
![]() ,
,
∵平面![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
……………………………………………2分
,
……………………………………………2分
∴可以以点![]() 为原点,以过
为原点,以过![]() 点平行于
点平行于![]() 的直线为
的直线为![]() 轴,分别以直线
轴,分别以直线![]() 和
和![]() 为
为![]() 轴和
轴和![]() 轴,建立如图所示的空间直角坐标系
轴,建立如图所示的空间直角坐标系![]() .
.
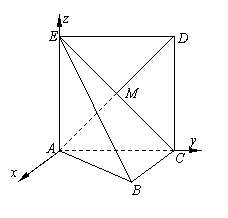 设
设![]() ,则
,则
![]()
![]() ,
,
![]() 是正方形
是正方形![]() 的对角线的交点,
的对角线的交点,
![]() .…………………………………4分
.…………………………………4分
(Ⅰ)![]()
![]() ,
,![]() ,
,![]() ,
,
![]() ,
………………………………………6分
,
………………………………………6分
![]()
![]() 平面
平面![]() .
……………………………………………7分
.
……………………………………………7分
(Ⅱ) ![]() 平面
平面![]() ,
,
![]() 为平面
为平面![]() 的一个法向量,
……………………………………………8分
的一个法向量,
……………………………………………8分
![]() ,
,
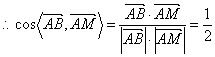 . ……………………………………………9分
. ……………………………………………9分
![]() .
.
∴直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() .
………………………………………10分
.
………………………………………10分
(Ⅲ) 设平面![]() 的法向量为
的法向量为![]() ,则
,则![]() 且
且![]() ,
,
![]() 且
且![]() .
.
![]() 即
即![]()
取![]() ,则
,则![]() , 则
, 则![]() . ……………………………………………12分
. ……………………………………………12分
又∵![]() 为平面
为平面![]() 的一个法向量,且
的一个法向量,且![]() ,
,
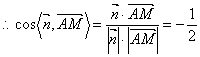 ,
,
设二面角![]() 的平面角为
的平面角为![]() ,则
,则![]() ,
,
![]() .
.
∴二面角![]() 等于
等于![]() .
……………………………………………14分
.
……………………………………………14分
19.(本小题满分14分)
设![]() 是定义在
是定义在![]() 上的奇函数,且当
上的奇函数,且当![]() 时,
时, ![]()
![]() .
.
(Ⅰ)求函数![]() 的解析式;
的解析式;
(Ⅱ) 当![]() 时,求函数
时,求函数![]() 在
在![]() 上的最大值
上的最大值![]() ;
;
(Ⅲ)如果对满足![]() 的一切实数
的一切实数![]() ,函数
,函数![]() 在
在![]() 上恒有
上恒有![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
解: (Ⅰ)当![]() 时,
时, ![]() ,则
,则
![]()
![]() .
……………………………2分
.
……………………………2分
当![]() 时,
时, ![]()
![]() .
……………………………3分
.
……………………………3分
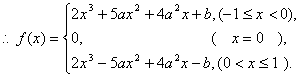 …………………………4分
…………………………4分
(Ⅱ)当![]() 时
时
![]()
![]()
![]() .
………5分
.
………5分
(1)当![]() ,即
,即![]() 时
时
当![]() 时,
时,![]() , 当
, 当![]() 时,
时,![]() ,
,
![]() 在
在![]() 单调递增,在
单调递增,在![]() 上单调递减,
上单调递减,
![]() .
……………………………7分
.
……………………………7分
(2)当![]() ,即
,即![]() 时,
时,![]() ,
,
![]() 在
在![]() 单调递增.
单调递增.
![]() ,
……………………………9分
,
……………………………9分
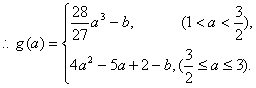 ……………………………10分
……………………………10分
(Ⅲ) 要使函数![]() 在
在![]() 上恒有
上恒有![]() ,必须使
,必须使![]() 在
在![]() 上的最大值
上的最大值![]() .
.
也即是对满足![]() 的实数
的实数![]() ,
,![]() 的最大值要小于或等于
的最大值要小于或等于![]() . ………………11分
. ………………11分
(1)当![]() 时,
时,![]() ,此时
,此时![]() 在
在![]() 上是增函数,
上是增函数,
则![]()
![]()
![]() .
.
![]() ,解得
,解得![]() . ………①
………………………………12分
. ………①
………………………………12分
(2)当![]() 时,
时,![]()
此时,![]() 在
在![]() 上是增函数,
上是增函数, ![]() 的最大值是
的最大值是![]() .
.
![]() ,解得
,解得![]() .………②
……………………………13分
.………②
……………………………13分
由①、②得实数![]() 的取值范围是
的取值范围是![]() .
……………………………14分
.
……………………………14分
20.(本小题满分14分)
已知椭圆![]() 的中心为原点,点
的中心为原点,点![]()
![]() 是它的一个焦点,直线
是它的一个焦点,直线![]() 过点
过点![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,且当直线
两点,且当直线![]() 垂直于
垂直于![]() 轴时,
轴时,![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)是否存在直线![]() ,使得在椭圆
,使得在椭圆![]() 的右准线上可以找到一点
的右准线上可以找到一点![]() ,满足
,满足![]() 为正三角形.如果存在,求出直线
为正三角形.如果存在,求出直线![]() 的方程;如果不存在,请说明理由.
的方程;如果不存在,请说明理由.
解:(Ⅰ)设椭圆![]() 的方程为:
的方程为:![]() ,则
,则![]() .……①……1分
.……①……1分
![]() 当
当![]() 垂直于
垂直于![]() 轴时,
轴时,![]() 两点坐标分别是
两点坐标分别是![]() 和
和![]() ,
,
![]() ,则
,则![]() ,即
,即![]() .………② …3分
.………② …3分
由①,②消去![]() ,得
,得![]() .
.
![]() 或
或![]() (舍去).
(舍去).
当![]() 时,
时,![]() .
.
因此,椭圆![]() 的方程为
的方程为![]() .
……………………………5分
.
……………………………5分
(Ⅱ)设存在满足条件的直线![]() .
.
(1)当直线![]() 垂直于
垂直于![]() 轴时,由(Ⅰ)的解答可知
轴时,由(Ⅰ)的解答可知![]() ,焦点
,焦点![]() 到右准线的距离为
到右准线的距离为![]() ,此时不满足
,此时不满足![]() .
.
因此,当直线![]() 垂直于
垂直于![]() 轴时不满足条件.
……………………………7分
轴时不满足条件.
……………………………7分
(2)当直线![]() 不垂直于
不垂直于![]() 轴时,设直线
轴时,设直线![]() 的斜率为
的斜率为![]() ,则直线
,则直线![]() 的方程为
的方程为![]() .
.
由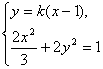
![]()
![]() ,
,
设![]() 两点的坐标分别为
两点的坐标分别为![]() 和
和![]() ,则
,则
![]() ,
,![]() .
.
![]()
![]()
![]() . ……………………9分
. ……………………9分
又设![]() 的中点为
的中点为![]() ,则
,则![]()
![]() .
.
当![]() 为正三角形时,直线
为正三角形时,直线![]() 的斜率为
的斜率为![]() .
.
![]() ,
,
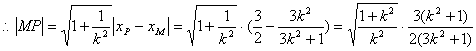 .
.
…………………………11分
当![]() 为正三角形时,
为正三角形时,![]() ,即
,即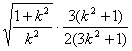 =
=![]() ,
,
解得![]() ,
,![]() .
…………………………13分
.
…………………………13分
因此,满足条件的直线![]() 存在,且直线
存在,且直线![]() 的方程为
的方程为![]() 或
或![]() .……14分
.……14分
21.(本小题满分14分)已知数列![]() 满足
满足![]() ,
,![]() .
.
(Ⅰ)试判断数列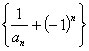 是否为等比数列,并说明理由;
是否为等比数列,并说明理由;
(Ⅱ)设![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(Ⅲ)设![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() .求证:对任意的
.求证:对任意的![]() ,
,![]() .
.
解:(Ⅰ)![]() ,
,![]() ,……………3分
,……………3分
又![]() ,
,![]() 数列
数列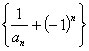 是首项为
是首项为![]() ,公比为
,公比为![]() 的等比数列.……5分
的等比数列.……5分
(Ⅱ)依(Ⅰ)的结论有![]() ,即
,即![]() .………………6分
.………………6分
![]() .
.
![]() . ………………9分
. ………………9分
(Ⅲ)![]() ,
,
![]() .
……………………10分
.
……………………10分
当![]() 时,则
时,则![]()
![]()
![]()
![]() .
.
![]() ,
, ![]() 对任意的
对任意的![]() ,
,![]() .
………………………14分
.
………………………14分
命题:喻秋生 李志敏 程武军 审题:石永生