湖北省武汉市2007届高三年级调研考试
文科数学试题
本试卷150分，考试用时120分钟。
注意事项：
1．本卷1—10题为选择题，共50分；11—21题为非选择题，共100分。请把答案全部写在答题卷上，答在试题卷上无效。考试结束后，监考人员将答案卷收回。
2．答卷前，考生务必将自己的学校、班级、姓名、准考证号填写在试题卷和答题卷指定的位置。
3．选择题选出答案后，用2B铅笔把答题卷上对应题目的答案标号涂黑。如需改动，请用橡皮擦干净后，再选涂其它答案标号。
4．非选择题请用0.5毫米黑色签字笔答在答题卷上每题所对应的答题区域内，答在指定区域外无效。
参考公式：
如果事件A、B互斥，那么P（A+B）=P（A）+P（B）
如果事件A、B相互独立，那么P（A · B）=P（A）·P（B）
如果事件A在一次试验中发生的概率是p，那么n次独立重复试验中恰好发生k次的概
率
.
球的表面积公式 
其中R表示球的半径
球的体积公式 
其中R表示球的半径
一、选择题：本大题共10题，每小题5分，共50分。在每小题给出的四个选项中，只有一项是符合题目要求的。
1．设全集U=R，集合M=
，则下列关系中正确的是 （ ）
A．M∩N=M B．M∩N=N C．M∪N=R D．M∪N=N
2．
的值是 （ ）
A．
B．－ C．
D．－
3．记函数
的反函数为
= （ ）
A．2 B．3 C．7 D．8
4．为了了解某校高三调考学生成绩，用简单随机抽样的方法从中抽取了100名学生的成绩进行统计分析，在这个问题中，100被称为 （ ）
A．总体 B．个体
C．从总体中抽取的一个样本 D．样本容量
5．已知两个非零向量
= （ ）
A．－3 B．－24 C．21 D．12
6．在等差数列
中，若
的值为 （ ）
A．15 B．16 C．17 D．18
7．若直线
始终平分圆
的圆周，则
的最小值是 （ ）
A．4 B．2 C．
D．
8．棱长为a的正四面体中，高为h，斜高为m，相对棱间的距离为d，则a、m、h、d的大小关系正确的是 （ ）
A．
B．
C．
D．
9．在锐角△ABC中，A>B, 则有下列不等式：①sinA>sinB；②cosA<cosB；③sin2A>sin2B；④cos2A<cos2B
A．①③ B．②③ C．①②③ D．①②④
10．定义在R上的函数
上是增函数，且函数
是奇函数，当
|
的值 （ ）
A．可能为0 B．恒大于0 C．恒小于0 D．可正可负
二、填空题：本大题共5小题，每小题5分，共25分.
11．不等式
的解集为
.
12．在
的展开式中，常数项为
.（用数字作答）
13．在约束条件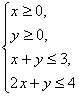
下，目标函数
的最大值是
.
14．直线AB过抛物线y2=x的焦点F，与抛物线交于A、B两点，且AB=3，则线段AB的中点到y轴的距离为 .
15．定义运算
的最小值是
.
三、解答题：本大题共6小题，共75分. 解答应写出文字说明、证明过程或演算步骤.
16．（本小题满分12分）
设函数
（1）求f（x）的单调递增区间；
（2）设
的值.
17．（本小题满分12分）
箱子中有红、黄两种颜色的卡片各4张，现有甲、乙两人从箱子中轮流抽取卡片，甲先抽，乙后抽，然后甲再抽，…，抽取后不放回，直到两人中有一人抽到红色卡片时就终止. 假设每张卡片在每一次被抽取的机会是等可能的.
（1）求甲恰好在第二次抽到红色卡片的概率；
（2）求甲抽到红色卡片的概率.
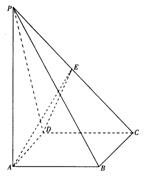
18．（本小题满分12分）
|
，E为CP的中点.
（1）求直线DE与平面ABCD所成角的大小.
（2）求二项角E—AD—C的正切值.
（3）在线段PC上是否存在一点M，使PC⊥平面MBD？
如果存在，求出MC的长；如果不存在，请说明理由.
19．（本小题满分12分）
已知单调递增的等比数列
、a4的等差中项.
（1）求数列的通项公式；
（2）若
的前n项和Tn.
20．（本小题满分13分）
已知函数
.
（1）求函数
的单调区间；
（2）当实数k在什么范围内变化时，函数
的图象与直线y=3只有一个公共点.
21．（本小题满分14分）
已知双曲线
，过上焦点F2的直线与下支交于A、B两点，且线段AF2、BF2的长度分别为m、n.
（1）写出直线AB的斜率k的取值范围；
（2）证明mn≥1；
（3）当直线AB的斜率
时，求mn的取值范围.
参考答案
一、选择题
1．B 2．C 3．C 4．D 5．C 6．B 7．A 8．A 9．D 10．B
|
11．
12．12 13．7 14．
15．1
三、解答题
16．（1）
…………3分
由
，得
单调增区间为
. …………6分
（2）由
平方得
…………12分
17．（1）记“甲恰好在第二次抽到红色卡片”的为事件A，则
…………4分
（2）甲抽到红色卡片分为三类：
第一类：甲第一次抽到红色卡片，概率为
第二类：甲第二次抽到红色卡片，概率为
第三类：甲第三次抽到红色卡片，概率为
；…………10分
所以，甲抽到红色卡片的概率为
…………12分
18．（1）如图，连结AC，BD交于点0，连结OE，则OE//PA.
∵PA⊥底面ABCD， ∴OE⊥面ABCD.
∠EDO为DE与平面ABCD所成的角. …………2wv
…………4分
（2）过点0作OF⊥AD于F，连结EF，由三垂线定理得EF⊥AD，
则∠EFO为二面角E—AD—C的平面角. …………6分
. …………8分
（3）过点O作OM⊥PC于M，由△COM~△CPA，得
. …………10分
∵PC⊥OM， ∴PC⊥面MBD.
所以，求M存在，且使CM=
. …………12分
方法二：向量法（参照给分）.
19．解：（1）由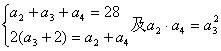
，解得
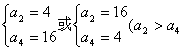不合题意，舍去）. …………4分
从而a1=2，q=2.
…………6分
（2）
. …………8分
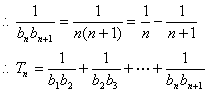
…………12分
20．解：（1）
由
. …………2分
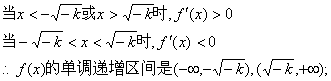
递减区间为
. …………6分
（2）由（1）知，当
，
当
…………8分
依题意，要使函数
只有一个公共点，须
…………10分
所以，所求实数k的取值范围是
. …………13分
21．解：（1）所求斜率的范围是
.
（说明：只要写出范围，不需考查过程） …………2分
（2）易知双曲线上焦点为
.
设直线AB的方程为
当k=0时，A、B两点的横坐标分别为1和－1，
此时mn=1. …………4分
当
代入双曲线方程，消去x得
. …………6分
由双曲线的第二定义，知
，
…………8分
所以，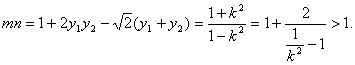
综上，知mn≥1. …………10分
（3）记
由（2）知，
解得
由
为所求. …………14分
欢迎访问 http://www.k12zy.com