湖北省武汉市2007届高三年级调研考试
理科数学试题
本试卷150分,考试用时120分钟。
注意事项:
1.本卷1—10题为选择题,共50分;11—21题为非选择题,共100分。请把答案全部写在答题卷上,答在试题卷上无效。考试结束后,监考人员将答案卷收回。
2.答卷前,考生务必将自己的学校、班级、姓名、准考证号填写在试题卷和答题卷指定的位置。
3.选择题选出答案后,用2B铅笔把答题卷上对应题目的答案标号涂黑。如需改动,请用橡皮擦干净后,再选涂其它答案标号。
4.非选择题请用0.5毫米黑色签字笔答在答题卷上每题所对应的答题区域内,答在指定区域外无效。
参考公式:
如果事件A、B互斥,那么P(A+B)=P(A)+P(B)
如果事件A、B相互独立,那么P(A · B)=P(A)·P(B)
如果事件A在一次试验中发生的概率是p,那么n次独立重复试验中恰好发生k次的概
率![]() .
.
球的表面积公式 ![]() 其中R表示球的半径
其中R表示球的半径
球的体积公式 ![]() 其中R表示球的半径
其中R表示球的半径
一、选择题:本大题共10题,每小题5分,共50分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.设集合![]() ,则实数a的取值范围是
,则实数a的取值范围是
( )
A.![]() B.
B.![]() C.(-1,+∞) D.(-∞,-1)
C.(-1,+∞) D.(-∞,-1)
2.若![]() 都是实数,i是虚数单位,则
都是实数,i是虚数单位,则![]() = ( )
= ( )
A.1+2i B.1-2 i C.2+ i D.2-i
3.已知![]() 的值应是 ( )
的值应是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.若函数![]() 的反函数为
的反函数为![]() ,则满足
,则满足![]() >1的x的集合是 ( )
>1的x的集合是 ( )
A.(0,+∞) B.(1,+∞) C.(-1,1) D.(0,1)
5.在抽查某产品尺寸过程中,将其尺寸分成若干组,[a,b]是其中的一组,已知该组上的直方图的高为h,则该组的频率为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.在等差数列![]() 中,若
中,若![]() 的值为 ( )
的值为 ( )
A.15 B.16 C.17 D.18
7.已知椭圆![]() 有相同的准线,则动点P(n,m)的轨迹为 ( )
有相同的准线,则动点P(n,m)的轨迹为 ( )
A.椭圆的一部分 B.双曲线的一部分
C.抛物线的一部分 D.直线的一部分
8.EF是两条互相垂直的异面直线m、n的公垂线段,点P是线段EF上除E、F外一动点,若点A是m上不同于垂足E的点,点B是n上不同于垂足F的点,则△ABP是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.以上均有可能
|
则![]() ( )
( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
|
A.可能为0 B.恒大于0 C.恒小于0 D.可正可负
二、填空题:本大题共5小题,每小题5分,共25分.
11.6人分乘两辆出租车,每车最多4人,则不同的乘车方法共有 种(填数字).
12.在![]() 的展开式中,x5的系数为
.
的展开式中,x5的系数为
.
13.在约束条件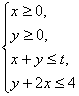 下,当
下,当![]() 时,目标函数
时,目标函数![]() 的最大的变化范围是
的最大的变化范围是
.
14.若函数![]() =
.
=
.
15.直线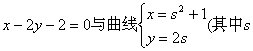 为参数)交于A、B两点,点M
是线段
为参数)交于A、B两点,点M
是线段
AB的中点,则点M到y轴的距离是 .
三、解答题:本大题共6小题,共75分. 解答应写出文字说明、证明过程或演算步骤.
|
已知向量![]() 其中
其中
![]() .
.
(1)求证:![]() ;
;
(2)![]() 的值域.
的值域.
17.(本小题满分12分)
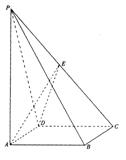
|
(1)求直线DE与平面PAC所成角;
(2)求二面角E—AD—C的大小;
(3)在线段PC上是否存在一点M,使PC⊥平面MBD成立?
如果存在,求出MC的长;如果不存在,请说明理由.
18.(本小题满分13分)
已知函数![]() .
.
(1)当![]() 时,判断函数
时,判断函数![]() 上的单调性;
上的单调性;
(2)当a=3时,求函数![]() 上的最大值.
上的最大值.
19.(本小题满分10分)
在一个单位中普查某种疾病,600个人去验血,对这些人的血的化验可以用两种方法进行:
方法一:每个人的血分别化验,这时需要化验600次;
方法二:把每个人的血样分成两份,取![]() 个人的血样各一份混在一起进行化验,如果结果是阴性的,那么对这k个人只作一次检验就够了;如果结果阳性的,那么再对这k个人的另一份血样逐个化验,这时对这k个人共需作k+1次化验.
个人的血样各一份混在一起进行化验,如果结果是阴性的,那么对这k个人只作一次检验就够了;如果结果阳性的,那么再对这k个人的另一份血样逐个化验,这时对这k个人共需作k+1次化验.
假定对所有的人来说,化验结果是阳性的概率是0.1,而且这些人的反应是独立的.将每个人的血样所需的检验次数作为随机变量![]() .
.
(1)写出方法二中随机变量![]() 的分布列,并求数学期望E
的分布列,并求数学期望E![]() (用k表示);
(用k表示);
(2)现有方法一和方法二中k分别取3、4、5共四种方案,请判断哪种方案最好,并说明理由.(参考数据:取0.93=0.729,0.94=0.656,0.95=0.591)
20.(本小题满分14分)
已知双曲线![]() ,过上焦点F2的直线与下支交于A、B两点,且线段AF2、BF2的长度分别为m、n.
,过上焦点F2的直线与下支交于A、B两点,且线段AF2、BF2的长度分别为m、n.
(1)证明mn≥1;
(2)若m>n,当直线AB的斜率![]() 时,求
时,求![]() 的取值范围.
的取值范围.
21.(本小题满分14分)
已知定义在R上的单调函数![]() ,存在实数x0,使得对于任意实数x1、x2,总有
,存在实数x0,使得对于任意实数x1、x2,总有
![]() 恒成立.
恒成立.
(1)求x0的值;
(2)若![]() 且对任意正整数n,有
且对任意正整数n,有![]()
![]() 的大小关系,
的大小关系,
并给出证明.
参考答案
一、选择题
1.B 2.C 3.B 4.A 5.D 6.B 7.A 8.C 9.A 10.C
|
11.50 12.-160 13.[7,8] 14.1 15.10
三、解答题
16.解:(1)![]() . …………4分
. …………4分
(2)![]()
![]() . …………8分
. …………8分
![]()
![]() …………12分
…………12分
17.解:(1)(1)如图,连结AC,BD交于点0,
∵PA⊥底面ABCD, ∴平面PAC⊥平面ABCD.
又∵底面ABCD是菱形 ∴BD⊥AC, ∴DO⊥面PAC.
连结OE,则∠DEO为DE与平面PAC所成的角 …………2分
![]()
![]() …………4分
…………4分
(2)过点0作OF⊥AD于F,连结EF,由三垂线定理得EF⊥AD,
则∠EFO为二面角E—AD—C的平面角. …………6分
![]() .
.
![]() …………8分
…………8分
(3)过点O作OM⊥PC于M,由△COM~△CPA,得
![]() . …………10分
. …………10分
∵PC在底面ABCD上的射影为AC,且AC⊥BD, ∴PC⊥BD.
又PC⊥OM, ∴PC⊥面MBD.
所以,求M存在,且使CM=![]() . …………12分
. …………12分
方法二:向量法(参照给分).
18.解:(1)![]()
![]() .
.
![]() 上是增函数. …………4分
上是增函数. …………4分
(2)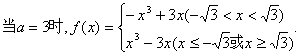 …………6分
…………6分
(i)当![]()
(ii)当![]()
当![]()
所以,![]() 的单调递增区间是
的单调递增区间是![]() 单调递减区间是
单调递减区间是![]() . …………8分
. …………8分
由上知,当x=1时,f(x)取得极大值f(1)=2
又b>1,由2=b3-3b,解得b=2. …………10分
|
当![]() 时取得最大值
时取得最大值![]() .
.
所以,函数![]() 上的最大值为
上的最大值为
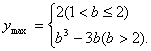 …………13分
…………13分
19.解:(1)对于方法二,k个人一组的混合血液呈阴性结果的概率为0.9k,呈阳性结果的概率为1-0.9k.
当k个人一组的混合血液呈阴性时,可以认为每个人需要化验的次数为![]() 次;当k个人一组的混合血液呈阳性时,可以认为每个人需要化验的次验为
次;当k个人一组的混合血液呈阳性时,可以认为每个人需要化验的次验为![]() +1次.
+1次.
所以
|
|
|
| ||
| P | 0.9k | 1-0.9k |
![]() …………5分
…………5分
(2)对方法一:![]() . …………6分
. …………6分
当k=3时,![]() ;
;
当k=4时,![]() ;
;
当k=5时,![]() . …………9分
. …………9分
比较知k=4时的方案最好 …………10分
20.解:(1)易知双曲线上焦点为![]() .
.
设直线AB的方程为![]()
当k=0时,A、B两点的横坐标分别为1和-1,
此时mn=1.
当![]() 代入双曲线方程,消去x得
代入双曲线方程,消去x得
![]() . …………2分
. …………2分
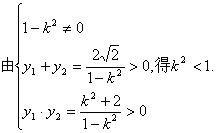 …………4分
…………4分
由双曲线的第二定义,知![]() ,
,
![]() …………8分
…………8分
∴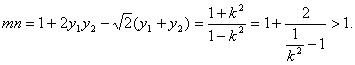
综上,知mn≥1. …………10分
(2)设直线AB的方程为![]() ,代入双曲线方程,消去y并整理得
,代入双曲线方程,消去y并整理得
![]()
![]() …………8分
…………8分
![]()
![]() ①
①
![]() ②
②
由①②,消去![]()
即![]() ③ …………12分
③ …………12分
由![]()
 即为所求. …………14分
即为所求. …………14分
21.解:(1)令![]()
![]() …………2分
…………2分
![]() 上的单调函数,且
上的单调函数,且![]()
![]() …………4分
…………4分
(2)由(1)得![]() . …………6分
. …………6分
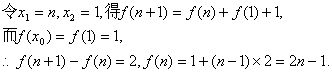
从而![]() …………8分
…………8分
![]() …………10分
…………10分
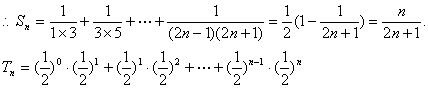
![]() …………12分
…………12分
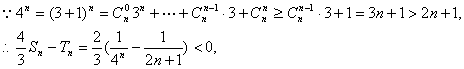
![]()
欢迎访问 http://www.k12zy.com