福建省诏安一中2007年高三教学质量检测
数 学 试 题（理科） 2007.06.1
考试时间：120分钟 满分：150分
参考公式：
如果事件A、B互斥，那么P（A+B）=P（A）+P（B）
如果事件A、B相互独立，那么P（A·B）=P（A）·P（B）
如果事件A在依次实验中发生的概率是P，那么n次独立重复实验中恰好发生k次的概率
球的体积公式V=
（其中R表示球的半径）
球的表面积公S=4
（其中R表示球的半径）
一、选择题：本题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的，把正确的代号填在指定位置上.
1．设集合U=R，集合P={xx2≥x}，Q={xx>0}，则下列关系中正确的是 （ ）
A．P∩Q
Q B．P∪QQ C．P∪Q≠R D．
P∩Q=
2．设复数
为纯虚数，则x= （ ）
A．－2 B．－1 C．1 D．2
3．函数
的反函数是 （ ）
A．
B．
C．
D．
4．设圆x2+y2－2x+6y+1=0上有关于直线2x+y+c=0对称的两点，则c的值为 （ ）
A．2 B．－1 C．－2 D．1
5．已知命题
，若
是
的必要不充分条件，则实数
的取值范围是（ ）
A．
B．
C．
D．
6．已知向量
=（2，3），
=（－4，7），那么在方向上的投影为 （ ）
A．
B．
C．
D．
7．若（x－）6的展开式中的第五项等于，则 （＋＋＋…＋）＝（ ）
A．1 B． C． D．
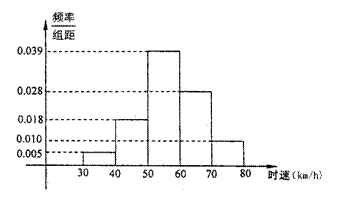8．200辆汽车正经过某一雷达地区，这些汽车运行的时速频率分布直方图如图所示，则时速超过60km/h的汽车数量约为( ) （ Ｂ ）
A．65辆 B．76辆
C．88辆 D．95辆
9．对于顶点在原点的抛物线，给出下列条件
① 焦点在x轴上；② 焦点在y轴上；③抛物线上横坐标为1的点到焦点的距离等于6；
④ 抛物线的通径长为5；⑤抛物线上点（2，a）到准线的距离为
．
能使这条抛物线方程为
的条件是（ ）
A．① ⑤ B．② ⑤ C．① ③ D．① ④
10．正三棱锥底面边长为a，侧棱与底面成角为60°，过底面一边作一截面使其与底面成30°的二面角，则此截面的面积为（ ）
A．a2 B．a2 C．a2 D．a2
|
|
的两条渐近线恰好是抛物线
的两条切线，则a的值为
（ ）
A．
B．
C．
D．
12．如果一对兔子每月能生产一对（一雌一雄）小兔子，而每一对小兔子在它出生的第三个月里，又能生产一对小兔子. 假定在不发生死亡的情况下，由一对初生的小兔子从第一个月开始，如果用
表示初生小兔子的对数，
表示第n个月的兔子总对数，
那么以下结论正确的是 （ ）
A．bn是n无关的常量
B．bn是n有关的变量，且既有最大值，又有最小值
C．bn是n有关的变量，且有最小值，但无最大值
D．bn是n有关的变量，且既有最大值，但无最小值
二、填空题：本大题共4小题，每小题4分，共16分，把正确答案填在答题卡中的横线上
13．某个班有45名学生，学校为了解他们的身体发育状况，决定分成男生、女生两部分采用分层抽样，现每个女生被抽取的概率为0.2 ，抽取了3 名女生，则男生应抽取 人
14．把点A（2，1）按向量=（－2，3）平移到B，此时点B分向量
（O为坐标原点）的比为－2，则C点的坐标为
.
15．随意安排甲、乙、丙3人在三天节日里值班，每人值班一天，则甲排在乙之前的概率为
.（用数字作答）
16．表面积为S的正八面体的各项点均在体积为
的球面上，则S的值为 .
三、解答题（本大题共6小题，共74分．解答应写出文字说明、证明过程或演算步骤）
17．（本小题满分12分）
已知△ABC的三个内角A，B，C所对的边分别是a，b，c，向量m＝（1，1－sinA），n＝（cosA,1），且
⊥
．
（1）求角A；
（2）若b＋c＝a，求sin（B＋）的值．
18．（本小题满分12分）
已知
（1）设函数y=f（x）在点
相切，求a的值；
（2）求函数f（x）的单调区间.
19．（本题满分12分）
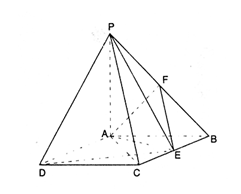如图：四棱锥P—ABCD中，底面ABCD是矩形，PA⊥底面ABCD，PA=AB=1，AD=
，点F是PB的中点，点E在边BC上移动.
（Ⅰ）点E为BC的中点时，试判断EF与平面PAC的位置关系，并说明理由；
（Ⅱ）证明：无论点E在BC边的何处，都有PE⊥AF;
（Ⅲ）当BE等于何值时，PA与平面PDE所成角的大小为45°．
20．（本题满分12分）
某集团准备兴办一所中学，投资1200万用于硬件建设.为了考虑社会效益和经济利益，对该地区教育市场进行调查，得出一组数据列表（以班为单位）如下：
| 班级学生数 | 配备教师数 | 硬件建设（万元） | 教师年薪（万元/人） | |
| 初中 | 60 | 2.0 | 28 | 1.2 |
| 高中 | 40 | 2.5 | 58 | 1.6 |
根据有关规定，除书本费、办公费外，初中生每年可收取学费600元，高中生每年可收取学费1500元.因生源和环境等条件限制，办学规模以20至30个班为宜.根据以上情况，请你合理规划办学规模使年利润最大，最大利润多少万元？（利润=学费收入－年薪支出）
21．（本小题满分12分）
椭圆C的中心为坐标原点O，焦点在y轴上，焦点到相应的准线的距离以及离心率均为，直线l与y轴交于点P（0，m），与椭圆C交于相异两点A、B，且
．
（1）求椭圆方程；
（2）若
，求m的取值范围．
22．（本小题满分14分）
已知函数
满足ax·=b+（ab≠0），f(1)=2，并且使=2x成立的实数x有且只有一个.
（Ⅰ）求f(x)的解析式；
（Ⅱ）若数列{an}前n项和为Sn，an满足
，求数列{an}
的通项公式；
（Ⅲ）当n∈N*，且n≥3时，在（II）的条件下，令
求证：
福建省诏安一中2007年高三教学质量检测
高 三 数 学 试 题（理科）（答 题 卷）2007.6.1
|
| 题 号 | 一 | 二 | 三 | 总分 | |||||
| 17 | 18 | 19 | 20 | 21 | 22 | ||||
| 得 分 | |||||||||
一、选择题：每小题5分，共60分．
| 题 号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案编号 |
|
13. 14.
15. 16.
三、解答题：本大题共6小题，共74分，解答要求写出文字说明、证明过程或推演步骤．
|
| 得分 | 评卷人 |
18．（本小题满分12分）
| 得分 | 评卷人 |
|
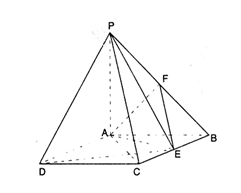
19. （本小题满分12分）
| 得分 | 评卷人 |
20.（本小题满分12分）
| 得分 | 评卷人 |
21.（本小题满分12分）
| 得分 | 评卷人 |
22.（本小题满分14分）
| 得分 | 评卷人 |