北京市宣武区2006-2007学年度第二学期第二次质量检测
高三数学（文） 2007．5
本试卷分第I卷（选择题）和第II卷（非选择题）两部分，满分150分，考试时间120分钟。
第I卷（选择题 共40分）
一. 选择题（本大题共有8个小题，每小题5分，共40分，在每小题给出的四个选项中，有且只有一个是符合题目要求的）
1. 集合
的真子集的个数是（ ）
A. 3 B. 4 C. 7 D. 8
2. 已知
，则sinα的值为（ ）
A. 
B.
C.
D.
3. “m=3”是“直线
和直线
不重合而平行”的（ ）
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
4. 若函数
的值域为［
］，则其反函数的值域为（ ）
A.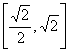 
B.
C. 
D.
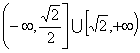
5. 使函数
递减且函数
递增的区间是（ ）
A. 
B.
C. 
D.
6. 已知两点
，
，动点
满足
，则动点P的轨迹方程为（ ）
A. 
B.
C. 
D.
7. 已知m，n表示两条直线，α表示一个平面，给出下列四个命题：
（1）
（2）
（3）
（4）
其中正确命题的序号是（ ）
A. ①② B. ②④ C. ①④ D. ②③
8. 点
在椭圆
的左准线上，过点P且方向向量
的光线，经过直线
反射后，通过椭圆的左焦点，则这个椭圆的离心率为（ ）
A. 
B.
C.
D.
第II卷（非选择题 共110分）
二. 填空题（本大题共6个小题，每小题5分，共30分）
9. 二项式
的展开式中的常数项为_____________________。
10. 设a、b都是单位向量，且a与b的夹角为60°，则
_________________，
______________________。
11. 不等式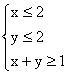
表示的平面区域的面积是____________________，
的最小值是_______________________。
12. 已知数列
的首项
，且满足
，则
=______________。
13. 某人的电子邮箱的密码由5位数字组成，为提高保密程度，他决定再插入两个英文字母a，b，原来的数字及顺序不变，则可构成新密码的个数为________________个。
14. 对于任意的两个实数对（a，b）和（c，d），规定：
，当且仅当a=c，b=d时成立。
运算“Ä”为：（a，b）Ä（c，d）=（ac－bd，bc+ad）
运算“Å”为：（a，b）Å（c，d）=（a+c，b+d）
现设p，q
，若（1，2）Ä（p，q）=（5，0），则（1，2）Å（p，q）=____________。
三. 解答题（本大题共6个小题，共80分，解答应写出文字说明，证明过程或演算步骤）
15. （本题满分13分）
在△ABC中，a，b，c分别是角A，B，C的对边，已知
，且
，
。求：
（1）角B；
（2）a+c的值。
16. （本题满分14分）
已知函数
（1）求函数
在
上的最大值和最小值；
（2）过点
作曲线
的切线，求此切线的方程。
17. （本题满分14分）
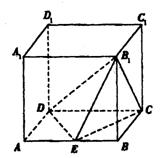
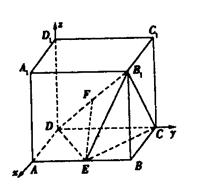
如图所示，在正方体
中，E为AB的中点。设正方体的棱长为2a。
（1）求AD和B1C所成的角；
（2）证明：平面EB1D⊥平面B1CD；
（3）求二面角E—B1C—D的斜弦值。
18. （本题满分13分）
甲、乙两人进行5次比赛，如果甲或乙无论谁胜了3次，则宣告比赛结束。假定甲获胜的概率是
，乙获胜的概率是，试求：
（1）比赛以甲3胜1败而宣告结束的概率；
（2）比赛以乙3胜2败而宣告结束的概率；
（3）设甲先胜3次的概率为a，乙先胜3次的概率为b，求a：b。
19. （本题满分13分）
设双曲线
的焦点分别为
、
，离心率为2。
（1）求此双曲线的渐近线l1、l2的方程；
（2）设A、B分别为l1、l2上的动点，且
，求线段AB中点M的轨迹方程，并说明是什么曲线。
20. （本题满分13分）
已知函数
（1）求的反函数
，并指出其定义域；
（2）若数列的前n项和
对所有的大于1的自然数n都有
，且
，求数列的通项公式；
（3）
，求
…+
。
北京市宣武区2006-2007学年度第二学期第二次质量检测
高三数学（文）参考答案 2007．5
一. 选择题（本大题共8个小题，每小题5分，共40分，在每个小题给出的四个选项中，有且只有一个是符合题目要求的。）
1. C 2. D 3. C 4. A
5. B 6. D 7. C 8. A
二. 填空题（本大题共6个小题，每小题5分，共30分。）
9. 24 10.
，
11.
，1
12. 
13.
42 14.
（2，0）
三. 解答题（本大题共6个小题，共80分，解答应写出文字说明，证明过程或演算步骤）
15. （本题满分13分）
解：（1）
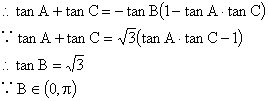
7分
（2）
且
，
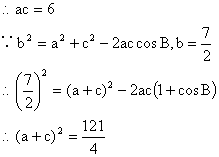
13分
16. （本题满分14分）
解：（1）
为函数的单调增区间
而当
时，
∴［-1，1］为f(x)的单调减区间
7分
（2）设切点为
，则所求切线方程为
由于切线过点
解得
所以切线方程为
即
14分
17. （本题满分14分）
解法一：（1）正方体中，AD//BC
∴AD与B1C所成的角为∠B1CB
∵∠B1CB=45°，∴AD和B1C所成的角为45° 3分
（2）取B1C的中点F，B1D的中点G，连结BF，EG，GF
∴CD⊥平面BCC1B1，且
∴DC⊥BF
又BF⊥B1C，
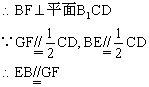
∴四边形BFGE是平行四边形
∴BF//GE
∴EG⊥平面B1CD
又EG
平面EB1D
∴平面EB1D⊥平面B1CD 8分
（3）连结EF
∵CD⊥B1C，GF//CD
∴GF⊥B1C
又EG⊥平面B1CD，EF⊥B1C
∴∠EFG为二面角E—B1C—D的平面角
∵正方体的棱长为2a
∴在△EFG中，GF=a，
即二面角
的余弦值为 14分
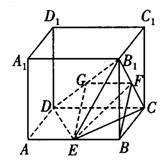
解法二：建立如图所示的空间直角坐标系
（1）
，A（2a，0，0），C（0，2a，0），
，
，
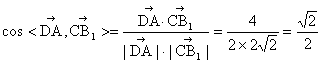
∴AD与B1C所成的角为45° 3分
（2）取B1D的中点F，连结EF
，
，
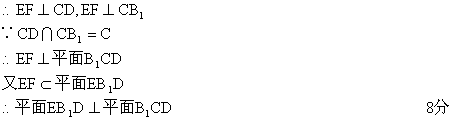
（3）设平面
的一个法向量
由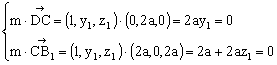
解得
又设平面B1CE的一个法向量为
由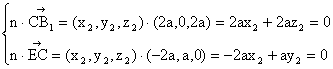
得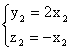
令
，则
14分
18. （本题满分13分）
解：（1）以甲3胜1负而结束比赛，则甲第4次必胜而前3次必有1次为败。
∴所求概率为
4分
（2）以乙3胜2负而结束比赛，则乙第5次必胜而前4次必有2次败
∴所求概率为
9分
（3）甲先胜3次的情况有3种：3胜无败、3胜1败、3胜2败，其概率分别为
，，
。
从而
故
13分
19. （本题满分13分）
解：（1）
，
∴双曲线方程为
∴渐近线方程为：
5分
（2）
，
设A在l1上，B在l2上，则设
，
①
设AB中点坐标为
，则
代入①，得
即
即所求轨迹为焦点在x轴上中心在原点的椭圆。 13分
20. （本题满分13分）
解：（1）
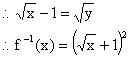
定义域为：
4分
（2）
又
，
故
8分
（3）
13分