北京市西城区2007年第二次抽样测试
高三数学试卷（理科）
本试卷分为第一卷（选择题）和第二卷（非选择题）两部分。共150分，考试时间120分钟.
第一卷（选择题 共40分）
一、选择题（本大题共8小题，每小题5分，共40分. 在每小题给出的四个选项中，只有一项是符合题目要求的.）
|
{1，2，3}，且A的元素中至少含有一个奇数，则满足条件的集合A共有
（ ）
A．6个 B．5个 C．4个 D．3个
2．若
的 （ ）
A．充分不必要条件 B．必要不充分条件
C．充要条件 D．既不充分也不必要条件
3．已知函数
的反函数. 若
的图象过点（3，4），则a等于 （ ）
A．
B．
C．
D．2
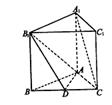
4．在正三棱锥P—ABC中，D，E分别是AB，BC的中点，有下列三个论断：
①
； ②AC//平面PDE； ③
.
其中正确论断的个数为 （ ）
A．0个 B．1个 C．2个 D．3个
5．若
的值为 （ ）
A．9 B．8 C．7 D．6
6．已知a，b是不共线的向量，
R）那么A，B，C三点共线的充要条件为 （ ）
A．
B．
C．
=－1 D．=1
7．设双曲线
的半焦距为c，离心率为
.若直线
与双曲线的一个交点的横坐标恰为c，则k等于 （ ）
|
B．
C．
D．
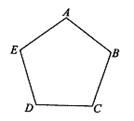
8．如图，正五边形ABCDE中，若把顶点A、B、C、D、E染上
红、黄、绿、三种颜色中的一种，使得相邻顶点所染颜色不
相同，则不同的染色方法共有 （ ）
A．30种 B．27种
C．24种 D．21种
第二卷（非选择题 共110分）
二、填空题（本大题共6小题，每小题5分，共30分. 把答案填在题中横线上.）
9．设甲、乙、丙三个加工厂共生产玩具6000件，其中甲厂生产了1440件. 现采用分层抽样的方法从三个加工厂抽取一个容量为500件的样本进行质量检测，则应从甲加工厂抽取
件玩具.
|
R，i是虚数单位，则
=
.
11．
=
.
12．设
R，函数
的最小值是－2，则实数k=
.
13．已知正四棱柱ABCD—A1B1C1D1的底面ABCD边长为1，高AA1=，它的八个顶点都在同一球面上，那么球的半径是
；A，B两点的球面距离为
.
14．按下列程序框图运算：
|
规定：程序运行到“判断结果是否大于244”为1次运算.
若x=5，则运算进行 次才停止；若运算进行k 
N*）次才停止，则x的取值范围是
.
三、解答题（本大题共6小题，共80分. 解答应写出文字说明，证明过程或演算步骤.）
15．（本小题满分12分）
已知
为第二象限的角，
为第三象限的角，
.
（I）求
的值.
（II）求
的值.
|
16．（本小题满分12分）
设甲、乙两套试验方案在一次试验中成功的概率均为p，且这两套试验方案中至少有一套试验成功的概率为0.51. 假设这两套试验方案在试验过程中，相互之间没有影响.
（I）求p的值；
（II）设试验成功的方案的个数为
，求的分布列及数学期望E.
|
17．（本小题满分14分）
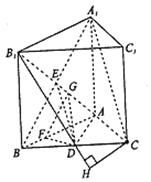
如图，正三棱柱ABC—A1B1C1中，D是BC的中点，AA1=AB=1.
（I）求证：A1C//平面AB1D；
（II）求二面角B—AB1—D的大小；
（III）求点c到平面AB1D的距离.
18．（本小题满分14分）
设直线
与椭圆
相交于A、B两个不同的点，与x轴相交于点C，记O为坐标原点.
（I）证明：
；
（II）若
的面积取得最大值时的椭圆方程.
|
19．（本小题满分14分）
设a>0，函数
.
（I）若
在区间
上是增函数，求a的取值范围；
（II）求在区间上的最大值.
20．（本小题满分14分）
设
是首项为1，公比为2的等比数列. 对于满足
的整数k,
数列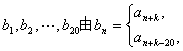
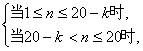确定. 记
.
（I）当k=1时，求M的值；
（II）求M的最小值及相应的k的值.
北京市西城区2007年第二次抽样测试
高三数学试卷（理科）参考答案
一、选择题：本大题共8小题，每小题5分，共40分.
|
二、填空题：本大题共6小题，每小题5分，共30分.
9．120 10．5 11．
12．
13．1（2分），
（3分）
14．4（2分），
（3分）
三、解答题：本大题共6小题，共80分，解答应写出文字说明，证明过程或演算步骤.
15．（本小题满分12分）
（I）解：因为α为第二象限的角，
，
所以，
，………………………………………2分
……………………………………………………… 4分
又
，
所以，
…………………………… 6分
（II）解：因为β为第三象限的角，，
所以，
…………………………………………8分
又
，………10分
所以，
………………12分
16．（本小题满分12分）
（I）解：记这两套试验方案在一次试验中均不成功的事件为A，则至少有一套试验成功的事件为
由题意，这两套试验方案在一次试验中不成功的概率均为1－p.
所以，
，
从而，
令
………………………………………6分
（II）解：ξ的可取值为0，1，2. ……………………………………………7分
……………………………………………………10分
所以ξ的分布列为
| ξ | 0 | 1 | 2 |
| P | 0.49 | 0.42 | 0.09 |
ξ的数学期望
……12分
|
解法一（I）证明：
连接A1B，设A1B∩AB1 = E，连接DE.
∵ABC—A1B1C1是正三棱柱，且AA1 = AB，
∴四边形A1ABB1是正方形，
∴E是A1B的中点，
又D是BC的中点，
∴DE∥A1C. ………………………… 3分
∵DE平面AB1D，A1C
平面AB1D，
∴A1C∥平面AB1D. ……………………4分
（II）解：在面ABC内作DF⊥AB于点F，在面A1ABB1内作FG⊥AB1于点G，连接DG.
∵平面A1ABB1⊥平面ABC， ∴DF⊥平面A1ABB1，
∴FG是DG在平面A1ABB1上的射影， ∵FG⊥AB1， ∴DG⊥AB1
∴∠FGD是二面角B—AB1—D的平面角 …………………………7分
设A1A = AB = 1，在正△ABC中，DF=
在△ABE中，
，
在Rt△DFG中，
，
所以，二面角B—AB1—D的大小为
…………………………9分
（III）解：∵平面B1BCC1⊥平面ABC，且AD⊥BC，
∴AD⊥平面B1BCC1，又AD平面AB1D，∴平面B1BCC1⊥平面AB1D.
在平面B1BCC1内作CH⊥B1D交B1D的延长线于点H，
则CH的长度就是点C到平面AB1D的距离. ……………………………12分
由△CDH∽△B1DB，得
即点C到平面AB1D的距离是
……………………………………14分
|
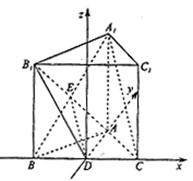
建立空间直角坐标系D—xyz，如图，
（I）证明：
连接A1B，设A1B∩AB1 = E，连接DE.
设A1A = AB = 1，
则
…………………………3分
，
……………………………………4分
（II）解：
， 
，
设
是平面AB1D的法向量，则
，
故
；
同理，可求得平面AB1B的法向量是
……………………7分
设二面角B—AB1—D的大小为θ，
，
∴二面角B—AB1—D的大小为
…………………………9分
（III）解由（II）得平面AB1D的法向量为
，
取其单位法向量
∴点C到平面AB1D的距离
……………………14分
18．（本小题满分14分）
（I）解：依题意，直线l显然不平行于坐标轴，故
将
，得
① ………………………… 3分
由直线l与椭圆相交于两个不同的点，得
，
即
…………………………………………………… 5分
（II）解：设
由①，得
因为
，代入上式，得
……………8分
于是，△OAB的面积 
………………11分
其中，上式取等号的条件是
……………………12分
由
将
这两组值分别代入①，均可解出
所以，△OAB的面积取得最大值的椭圆方程是
………………14分
19．（本小题满分14分）
（I）解：对函数
……………………… 2分
要使
上是增函数，只要
上恒成立，
即
上恒成立 ……………………………………4分
因为
上单调递减，所以上的最小值是，
注意到a > 0，所以a的取值范围是
……………………………………6分
（II）解：①当
时，由（I）知，上是增函数，
此时上的最大值是
……………………8分
②当
，
解得
……………………………………………………10分
因为
，
所以
上单调递减，
此时上的最大值是
………… 13分
综上，当时，上的最大值是
；
当
时，上的最大值是
……………14分
20．（本小题满分14分）
（I）解：显然
……………………………………1分
当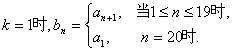
……………………………………3分
所以，
…………………………6分
（II）解：
………………………………………………9分
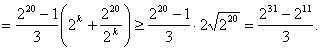………………12分
当
所以，M的最小值为
………………………………14分