2007年北京市海淀区数学二模理科试题
一、选择题:
1.若集合![]() ,则
,则![]() ( B
)
( B
)
A.![]() B.
B.![]() C.
C. ![]() D.
D.![]()
2.设![]() 、
、![]() 是不同的直线,
是不同的直线,![]() 、
、![]() 、
、![]() 是不同的平面,有以下四个命题:
是不同的平面,有以下四个命题:
①![]() ②
② ![]() ③
③![]() ④
④![]() ,
,
其中为真命题的是 ( C )
A. ①④ B. ②③ C. ①③ D.②④
3.“![]() ”是“函数
”是“函数![]() 的最小正周期为
的最小正周期为![]() ”的
( A )
”的
( A )
A.充分非必要条件 B.必要非充分条件 C.充分必要条件 D.既不充分也不必要条件
4.将圆![]() 按向量a
按向量a![]() 平移后,恰好与直线
平移后,恰好与直线![]() 相切,则实数
相切,则实数![]() 的值为 ( B )
的值为 ( B )
A ![]() B
B ![]() C
C ![]() D
D ![]()
5.在三角形![]() 中,
中,![]() ,
,![]() ,
,![]() ,则
,则![]() 的值为
( D )
的值为
( D )
A ![]() B
B ![]() C
C ![]() D
D ![]()

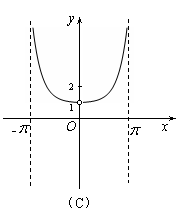
 6.函数
6.函数![]() 的图象可能是下列图象中的
( C )
的图象可能是下列图象中的
( C )
 |  |
![]()
7.以椭圆的右焦点![]() 为圆心作一个圆,使此圆过椭圆中心O并交椭圆于点M,N,若过椭圆左焦点
为圆心作一个圆,使此圆过椭圆中心O并交椭圆于点M,N,若过椭圆左焦点![]() 的直线MF1是圆
的直线MF1是圆![]() 的切线,则椭圆的右准线与圆
的切线,则椭圆的右准线与圆![]() ( A )
( A )
A.相交 B.相离 C.相切 D.位置关系随率心率改变
8.函数![]() (
(![]() )是常数,其图象是一条直线,称这个函数为线性函数.对于非线性可导函数
)是常数,其图象是一条直线,称这个函数为线性函数.对于非线性可导函数![]() ,在点
,在点![]() 附近一点
附近一点![]() 的函数值
的函数值![]() ,可以用如下方法求其近似代替值:
,可以用如下方法求其近似代替值:
![]() .
.
利用这一方法,![]() 的近似代替值
( A )
的近似代替值
( A )
(A)大于![]() (B)小于
(B)小于![]() (C)等于
(C)等于![]() (D)与
(D)与![]() 的大小关系无法确定
的大小关系无法确定
二、填空题:
9. 若 ![]() ,
, ![]() ,且
,且![]() 为纯虚数,则实数a的值为 -3
为纯虚数,则实数a的值为 -3
10.一个与球心距离为2的平面截球所得的圆面面积为![]() ,则球的表面积为 20
,则球的表面积为 20![]()
11.已知向量![]() =(4, 0),
=(4, 0),![]() =(2, 2),则
=(2, 2),则![]() = (-2,2) ;
= (-2,2) ;![]() 与
与![]() 的夹角的大小为 90°
的夹角的大小为 90°
12.已知函数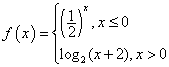 ,若
,若![]() ≥2,则
≥2,则![]() 的取值范围是
的取值范围是
13.有这样一种数学游戏:在![]() 的表格中,要求每个格子中都填上1、2、3三个数字中的某一个数字,且每一行和每一列都不能出现重复的数字,则此游戏共有 12 种不同的填法
的表格中,要求每个格子中都填上1、2、3三个数字中的某一个数字,且每一行和每一列都不能出现重复的数字,则此游戏共有 12 种不同的填法
14.数列{ a![]() },{ b
},{ b![]() }(
}(![]() )由下列条件所确定:
)由下列条件所确定:
(ⅰ)a1<0, b1>0 ;
(ⅱ)![]() ≥2时,ak与bk满足如下条件:
≥2时,ak与bk满足如下条件:
当![]() 时,ak= ak-1,
bk=
时,ak= ak-1,
bk=![]() ;
;
当![]() 时,ak=
时,ak= ![]() , bk=b k-1.
, bk=b k-1.
那么,当a1=-5,b1=5时, { a![]() }的通项公式为
}的通项公式为![]()
当b1> b2>…>bn(n≥2)时,用a1,b1表示{ bk }的通项公式为bk= (k=2,3…,n).
(1)![]() ;(2)
;(2)![]()
三、解答题:
15.(本小题12分)
已知![]() 为钝角,且
为钝角,且![]()
求: (Ⅰ)![]() ;
;
(Ⅱ)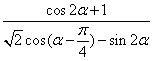 .
.
解: (Ⅰ)由已知:![]() …………………2分
…………………2分
得![]() …………………5分
…………………5分
(Ⅱ)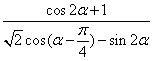
![]()
![]() …………………8分
…………………8分
∵![]() 且
且![]()
∴![]() …………………10分
…………………10分
∴![]()
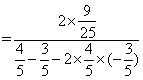
![]() …………………12分
…………………12分
16.(本小题13分)
某公司有10万元资金用于投资,如果投资甲项目,根据市场分析知道:一年后可能获利10﹪,可能损失10﹪,可能不赔不赚,这三种情况发生的概率分别为![]() ,
,![]() ,
,![]() ;如果投资乙项目,一年后可能获利20﹪,也可能损失20﹪,这两种情况发生的概率分别为
;如果投资乙项目,一年后可能获利20﹪,也可能损失20﹪,这两种情况发生的概率分别为![]() .
.
(Ⅰ)如果把10万元投资甲项目,用![]() 表示投资收益(收益=回收资金-投资资金),
表示投资收益(收益=回收资金-投资资金),
求![]() 的概率分布及
的概率分布及![]() ;
;
(Ⅱ)若把10万元投资投资乙项目的平均收益不低于投资甲项目的平均收益,求![]() 的取值范围.
的取值范围.
解:(Ⅰ)依题意,![]() 的可能取值为1,0,-1
…………1分
的可能取值为1,0,-1
…………1分
![]() 的分布列为
的分布列为
|
| 1 | 0 |
|
| p |
|
|
|
…………4分
![]() =
=![]()
![]() =
=![]() …………6分
…………6分
(Ⅱ)设![]() 表示10万元投资乙项目的收益,则
表示10万元投资乙项目的收益,则![]() 的分布列为
的分布列为
|
| 2 |
|
| p |
|
|
…………8分
![]() …………10分
…………10分
依题意要求
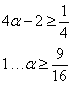 …………13分
…………13分
注:只写出![]() 扣1分
扣1分
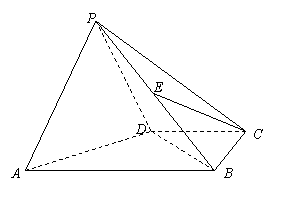 17.(本小题13分)
17.(本小题13分)
如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD, ![]() ,
,![]() ,E是BD的中点.
,E是BD的中点.
(Ⅰ)求证:EC//平面APD;
(Ⅱ)求BP与平面ABCD所成角的正切值;
(Ⅲ) 求二面角P-AB-D的大小.
解法一:(Ⅰ)如图,取PA中点F,连结EF、FD,
∵E是BP的中点,
∵EF//AB且![]() ,
,
又∵![]()
∴EF![]() DC∴四边形EFDC是平行四边形,故得EC//FD
…………2分
DC∴四边形EFDC是平行四边形,故得EC//FD
…………2分
又∵EC![]() 平面PAD,FD
平面PAD,FD![]() 平面PAD
平面PAD
∴EC//平面ADE …………4分
(Ⅱ)取AD中点H,连结PH,因为PA=PD,所以PH⊥AD
∵平面PAD⊥平面ABCD于AD
∴PH⊥面ABCD
∴HB是PB在平面ABCD内的射影
∴∠PBH是PB与平面ABCD所成角 …………6分
∵四边形ABCD中,![]()
 ∴四边形ABCD是直角梯形
∴四边形ABCD是直角梯形
![]()
设AB=2a,则![]() ,
,
在![]() 中,易得
中,易得![]() ,
,![]()
![]() ,
,
又∵![]() ,
,
∴![]() 是等腰直角三角形,
是等腰直角三角形,![]()
∴![]()
∴在![]() 中,
中,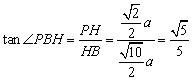 …………10分
…………10分
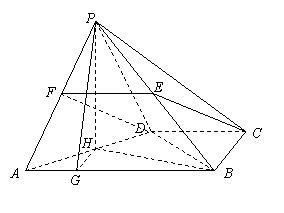
(Ⅲ)在平面ABCD内过点H作AB的垂线交AB于G点,连结PG,则HG是PG在平面ABCD上的射影,故PG⊥AB,所以∠PGH是二面角P-AB-D的平面角,由AB=2a …………11分
![]() ,又
,又![]() ∴
∴![]()
在![]() 中,
中,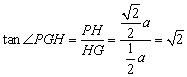 13分
13分
∴二面角P-AB-D的大小为![]() …………14分
…………14分
解法二:(Ⅰ)同解法一 4分
(Ⅱ)设AB=2a,同解法一中的(Ⅱ)可得
![]()
如图,以D点为原点,DA所在直线为x轴,DB所在直线为y轴,过D点且垂直于平面ABCD的直线为z轴建立空间直角坐标系. …………5分
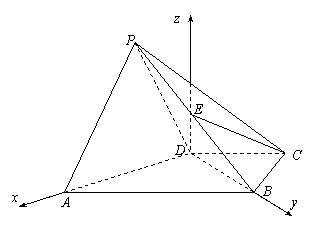 则
则![]() ,
,![]() ,则
,则![]() ,平面ABCD的一个法向量为m=(0,0,1), …………7分
,平面ABCD的一个法向量为m=(0,0,1), …………7分
所以,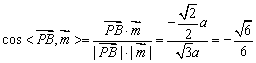
可得PB与平面ABCD所成角的正弦值为![]()
所以 PB与平面ABCD所成角的正切值为![]() …………10分
…………10分
(Ⅲ)易知![]() ,则
,则![]() ,设平面PAB的一个法向量为
,设平面PAB的一个法向量为![]() ,则
,则
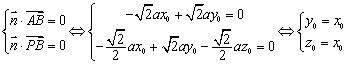 ,令
,令![]() ,可得
,可得![]() ……12分
……12分
得![]() ,
,
所以二面角P-AB-D的大小为![]() …………14分
…………14分
18.(本小题13分)
已知:![]()
![]() ,
,![]() .
.
(I)求![]() 、
、![]() 、
、![]() ;
;
(II)求数列![]() 的通项公式;
的通项公式;
(II)求证:![]()
解:(I)由已知![]() ,所以
,所以![]() 1分
1分
![]() ,所以
,所以![]()
![]() ,所以
,所以![]() 3分
3分
(II)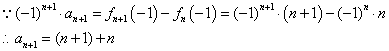
即![]()
所以对于任意的![]() ,
, ![]() 7分
7分
(III)![]()
∴![]() ①
①
![]() ②
②
①─②,得
![]() 9分
9分
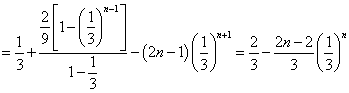
∴![]() ,
12分
,
12分
又![]() =1,2,3…,故
=1,2,3…,故![]() < 1
13分
< 1
13分
 19.(本小题14分)
19.(本小题14分)
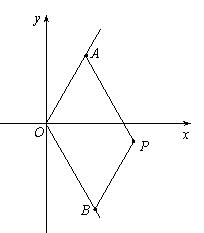
如图,
![]() 和
和![]() 两点分别在射线OS、OT上移动,且
两点分别在射线OS、OT上移动,且![]() ,O为坐标原点,动点P满足
,O为坐标原点,动点P满足![]() .
.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)求P点的轨迹C的方程,并说明它表示怎样
的曲线?
(Ⅲ)若直线l过点E(2,0)交(Ⅱ)中曲线C于M、N两
点,且![]() ,求l的方程.
,求l的方程.
解:(Ⅰ)由已知得
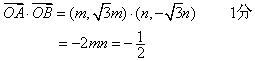
![]() …………4分
…………4分
(Ⅱ)设P点坐标为(x,y)(x>0),由![]() 得
得
![]()
![]() …………5分
…………5分
∴ 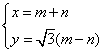 消去m,n可得
消去m,n可得
![]() ,又因
,又因![]() 8分
8分
∴ P点的轨迹方程为![]()
它表示以坐标原点为中心,焦点在![]() 轴上,且实轴长为2,焦距为4的双曲线
轴上,且实轴长为2,焦距为4的双曲线
![]() 的右支
…………9分
的右支
…………9分
(Ⅲ)设直线l的方程为![]() ,将其代入C的方程得
,将其代入C的方程得
![]()
即 ![]()
易知![]() (否则,直线l的斜率为
(否则,直线l的斜率为![]() ,它与渐近线平行,不符合题意)
,它与渐近线平行,不符合题意)
又![]()
设![]() ,则
,则![]()
∵ l与C的两个交点![]() 在
在![]() 轴的右侧
轴的右侧
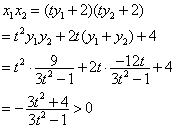
∴ ![]() ,即
,即![]()
又由 ![]() 同理可得
同理可得 ![]() …………11分
…………11分
由![]() 得
得
![]()
∴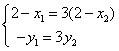
由![]() 得
得
![]()
由![]() 得
得
![]()
消去![]() 得
得 ![]()
解之得:![]() ,满足
,满足![]() …………13分
…………13分
故所求直线l存在,其方程为:![]() 或
或![]() …………14分
…………14分
20.(本小题14分)
设关于x的方程![]() 有两个实根
有两个实根![]() 、
、![]() ,且
,且![]() .定义函数
.定义函数![]()
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)判断![]() 在区间
在区间![]() 上的单调性,并加以证明;
上的单调性,并加以证明;
(Ⅲ)若![]() 为正实数,证明不等式:
为正实数,证明不等式:![]()
(Ⅰ)解:∵![]() 是方程
是方程![]() 的两个实根
的两个实根
∴![]()
∴![]()
同理![]()
∴![]() …………3分
…………3分
(Ⅱ)∵![]()
∴![]() …………4分
…………4分
当![]() 时,
时,![]() …………5分
…………5分
而![]()
∴![]() 在
在![]() 上为增函数
…………7分
上为增函数
…………7分
(Ⅲ)∵![]() 且
且![]()
∴![]()
![]()
∴![]() …………9分
…………9分
由(Ⅱ)可知![]()
同理可得![]() …………10分
…………10分
∴![]()
∴![]() …………12分
…………12分
又由(Ⅰ)知![]()
∴![]()
所以 ![]() …………14分
…………14分