北京市宣武区2006-2007学年度第二学期第二次质量检测
高三数学(理) 2007.5
本试卷分第I卷(选择题)和第II卷(非选择题)两部分,满分150分,考试时间120分钟。
第I卷(选择题 共40分)
一、选择题(本大题共有8个小题,每小题5分,共40分,在每小题给出的四个选项中,有且只有一个是符合题目要求的)
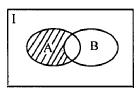
1. 如图,阴影部分所表示的集合是( )
A. ![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
2. “m=3”是“直线![]() 和直线
和直线![]() 不重合而平行”的( )
不重合而平行”的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
3. 设a,b都是单位向量,且a与b的夹角为60°,且a+b=( )
A. 2 B.
3 C.
![]() D.
D.
![]()
4. 要完成下列两项调查:①从某社区125户高收入家庭,280户中等收入家庭,95户低收入家庭中选出100户调查社会购买力的某项指标;②从某中学高一年级的12名体育特长生中选出3人调查学习负担情况。应采用的抽样方法是( )
A. ①用随机抽样法,②用系统抽样法
B. ①用分层抽样法,②用随机抽样法
C. ①用系统抽样法,②用分层抽样法
D. ①、②都用分层抽样法
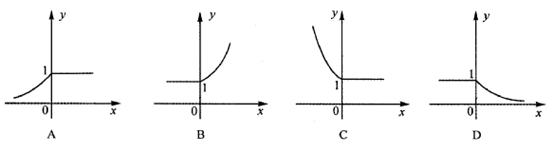
5. 定义运算![]() ,则函数
,则函数![]() 的图象大致为( )
的图象大致为( )
6. 已知m,n表示两条直线,α表示一个平面,给出下列四个命题:
①![]() ②
②![]()
③![]() ④
④![]()
其中正确命题的序号是( )
A. ①② B. ②④ C. ①④ D. ②③
7. 点P(-3,-1)在椭圆![]() (a>b>0)的左准线上,过点P且方向向量为m=(2,5)的光线,经过直线y=2反射后,通过椭圆的左焦点,则这个椭圆的离心率为( )
(a>b>0)的左准线上,过点P且方向向量为m=(2,5)的光线,经过直线y=2反射后,通过椭圆的左焦点,则这个椭圆的离心率为( )
A. ![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
8. 对于任意函数f(x),![]() ,可按如图所示构造一个数列发生器,其工作原理如下:
,可按如图所示构造一个数列发生器,其工作原理如下:
①输入数据![]() ,经过数列发生器输出
,经过数列发生器输出![]() ;
;
②若![]() ,则数列发生器结束工作;
,则数列发生器结束工作;
若![]() ,则将
,则将![]() 反馈回输入端,再输出
反馈回输入端,再输出![]() ,依此类推。
,依此类推。
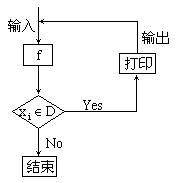
现给出![]() ,D=(0,1000)。若输入
,D=(0,1000)。若输入![]() ,则发生器结束工作时,输出数据的总个数为( )
,则发生器结束工作时,输出数据的总个数为( )
A. 8 B. 9 C. 10 D. 11
第II卷(非选择题 共110分)
二、填空题(本大题共6个小题,每小题5分,共30分)
9. 二项式![]() 的展开式中的常数项为_____________。
的展开式中的常数项为_____________。
10. 函数![]() 的最小正周期为_____________,此函数的值域为_____________。
的最小正周期为_____________,此函数的值域为_____________。
11. 不等式组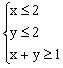 表示的平面区域的面积是_____________,
表示的平面区域的面积是_____________,![]() 的最小值是_____________。
的最小值是_____________。
12. 设A为圆![]() 上一动点,PA为圆的切线,且PA=1,则P点的轨迹方程为_____________。
上一动点,PA为圆的切线,且PA=1,则P点的轨迹方程为_____________。
13. A、B之间有6条网线路并联,它们通过的最大信息量分别为1,1,2,2,3,4,现从中任取三条网线,且使这三条网线通过的最大信息量的和不小于6的取法共有_____________种。
14. 对于任意的两个实数对(a,b)和(c,d),规定:
(a,b)=(c,d),当且仅当a=c,b=d时成立,
运算“![]() ”为:(a,b)
”为:(a,b)![]() (c,d)=(ac-bd,bc+ad)
(c,d)=(ac-bd,bc+ad)
运算“![]() ”为:(a,b)
”为:(a,b)![]() (c,d)=(a+c,b+d)
(c,d)=(a+c,b+d)
设![]() ,若(1,2)
,若(1,2)![]() (p,q)=(5,0),则(1,2)
(p,q)=(5,0),则(1,2)![]() (p,q)=_____________。
(p,q)=_____________。
三、解答题(本大题共6个小题共80分,解答应写出文字说明,证明过程或演算步骤)
15. (本题满分13分)
在△ABC中,a,b,c分别是角A,B,C的对边,已知![]() ,
,![]() ,
,![]() 。
。
求:(1)![]() 的值;
的值;
(2)△ABC中的最大内角。
16. (本题满分14分)
已知函数![]()
(1)求函数f(x)在![]() 上的最大值和最小值;
上的最大值和最小值;
(2)过点P(2,-6)作曲线![]() 的切线,求此切线的方程。
的切线,求此切线的方程。
17. (本题满分14分)
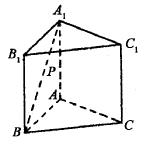
如图,已知正三棱柱![]() 的各条棱长都为a,P为
的各条棱长都为a,P为![]() 上的点。
上的点。
(1)试确定![]() 的值,使得PC⊥AB;
的值,使得PC⊥AB;
(2)若![]() ,求二面角P—AC—B的大小;
,求二面角P—AC—B的大小;
(3)在(2)的条件下,求![]() 到平面PAC的距离。
到平面PAC的距离。
18. (本题满分13分)
一次考试共有12道选择题,每道选择题都有4个选项,其中有且只有一个是正确的。评分标准规定:“每题只选一个选项,答对得5分,不答或答错得零分”。某考生已确定有8道题的答案是正确的,其余题中:有两道题都可判断两个选项是错误的,有一道题可判断一个选项是错误的,还有一道题因不理解题意只好乱猜。请求该考生:
(1)得60分的概率;
(2)得多少分的可能性最大?
(3)所得分数![]() 的数学期望。
的数学期望。
19. (本题满分13分)
双曲线C与椭圆![]() 有相同的焦点,直线
有相同的焦点,直线![]() 为C的一条渐近线。
为C的一条渐近线。
(1)求双曲线C的方程;
(2)过点P(0,4)的直线l交双曲线C于A、B两点,交x轴于Q点(Q点与C的顶点不重合),当![]() ,且
,且![]() 时,求Q点的坐标。
时,求Q点的坐标。
20. (本题满分13分)
已知f(x)是定义在(0,![]() )上的单调递增函数,对于任意的m、n(m、n
)上的单调递增函数,对于任意的m、n(m、n![]() )满足
)满足![]() ,且a、b(
,且a、b(![]() )满足
)满足![]() 。
。
(1)求f(1);
(2)若f(2)=1,解不等式f(x)<2;
(3)求证:![]() 。
。
北京市宣武区2006-2007学年度第二学期第二次质量检测
高三数学(理)参考答案 2007.5
一、选择题(本大题共有8个小题,每小题5分,共40分,在每个小题给出的四个选项中,有且只有一个是符合题目要求的。)
1. B 2. C 3. D 4. B
5. A 6. C 7. A 8. A
二、填空题(本大题共6个小题,每小题5分,共30分。)
9. 24 10.
![]() ,[
,[![]() ] 11.
] 11.
![]() ,1
,1
12. ![]() 13. 15 14.
(2,0)
13. 15 14.
(2,0)
三、解答题(本大题共6个小题,共80分,解答应写出文字说明,证明过程或演算步骤。)
15. (本题满分13分)
解:(1)∵![]()
∴![]()
∵![]()
∴![]()
∵![]() ∴
∴![]() …………………………4分
…………………………4分
∵![]() ,且
,且![]() ,
,![]()
∴ac=6
∵![]()
∴![]()
∴![]()
∵![]()
∴![]() ……………………8分
……………………8分
(2)不妨设![]()
∵![]()
∴![]()
由余弦定理,得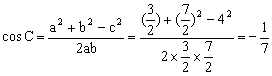
∴△ABC的最大内角为![]() ……………………13分
……………………13分
16. (本题满分14分)
解:(1)![]()
当![]() 时,
时,![]()
∴[-3,-1],[1,![]() ]为函数f(x)的单调增区间
]为函数f(x)的单调增区间
当![]() 时,
时,![]()
∴[-1,1]为函数f(x)的单调减区间
又∵![]()
∴当![]() 时,
时,![]()
当x=-1时,![]() ………………7分
………………7分
(2)设切点为Q(![]() ),则所求切线方程为
),则所求切线方程为
![]()
由于切线过点P(2,-6)
∴![]()
解得![]()
所以切线方程为![]()
即![]() ……………………14分
……………………14分
17. (本题满分14分)
解法一:(1)当![]() 时,PC⊥AB
时,PC⊥AB
取AB的中点D',连结CD'、PD'
∵△ABC为正三角形 ∴CD'⊥AB
当P为A1B的中点时,PD'//A1A
∵A1A⊥底面ABC,∴PD'⊥底面ABC
∴PC⊥AB………………………………5分
(2)当![]() 时,过P作PD⊥AB于D
时,过P作PD⊥AB于D
如图所示,则PD⊥底面ABC
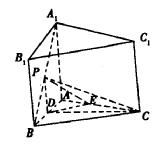
过D作DE⊥AC于E,连结PE,则PE⊥AC
∴∠DEP为二面角P—AC—B的平面角
又∵PD//A1A ∴![]() ∴
∴![]()
∴![]()
又∵![]() ,∴PD=
,∴PD=![]()
∴tan∠PED=![]() ,∴∠PED=60°
,∴∠PED=60°
即二面角P—AC—B的大小为60°……………………10分
(3)设C1到面PAC的距离为d,则![]()
∵PD//A1A ∴PD//平面A1C ∴DE即为P点到平面A1C的距离
又![]()
∴![]()
即![]()
解得![]()
即C1到平面PAC的距离为![]() …………………………14分
…………………………14分
解法二:以A为原点,AB为x轴,过A点与AB垂直的直线为y轴,AA1为z轴,建立空间直角坐标系A—xyz,如图所示,则B(a,0,0),A1(0,0,a),C(![]() ,
,![]() ,0),设P(x,0,z)
,0),设P(x,0,z)
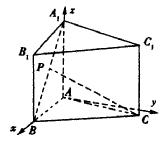
(1)由![]() ,得
,得![]()
即![]() ,∴P为A1B的中点
,∴P为A1B的中点
即![]() 时,PC⊥AB……………………5分
时,PC⊥AB……………………5分
(2)当![]() 时,由
时,由![]() ,得(x,0,z-a)
,得(x,0,z-a)![]()
即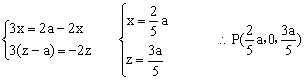
设平面PAC的一个法向量![]()
则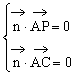 ,即
,即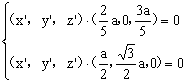
即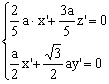
取![]() ,则
,则![]()
∴![]()
又平面ABC的一个法向量为![]()
∴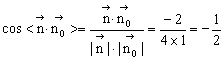
∴二面角P—AC—B的大小为180°-120°=60°………………10分
(3)设C1到平面PAC的距离为d
则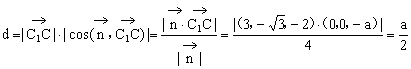
即C1到平面PAC的距离为![]() ……………………14分
……………………14分
18. (本题满分13分)
解:(1)设“有两道题可判断两个选项是错误的”选对的为事件A,“有一道题可判断一个选项是错误的”选对的为事件B,“有一道题不理解题意”选对的为事件C
∴![]()
所以,得60分的概率为![]() ……………………3分
……………………3分
(2)得40分的概率为![]()
得45分的概率为![]() ;
;
得50分的概率为![]()
![]() ;
;
得55分的概率为![]()
得45分或50分的可能性最大……………………9分
(3)![]() …………13分
…………13分
19. (本题满分13分)
解:(1)设双曲线方程为![]() 。由椭圆
。由椭圆![]() ,求得两焦点为(-2,0),(2,0)
,求得两焦点为(-2,0),(2,0)
∴对于双曲线C:c=2,又![]() 为双曲线C的一条渐近线
为双曲线C的一条渐近线
∴![]() 解得
解得![]()
∴双曲线C的方程为![]() ………………5分
………………5分
(2)解法一:由题意知直线l的斜率k存在且不等于零
设l的方程:![]() ,A(x1,y1),B(x2,y2)则Q(
,A(x1,y1),B(x2,y2)则Q(![]() ,0)
,0)
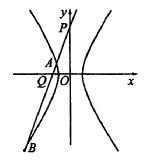
∵![]()
∴![]()
∴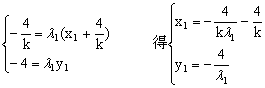
∵A(x1,y1)在双曲线C上,∴![]()
∴![]()
∴![]()
同理有:![]()
若![]() ,则直线l过顶点,不合题意
,则直线l过顶点,不合题意
∴![]()
∴![]() 是二次方程
是二次方程![]() 的两根
的两根
∴![]()
∴![]() ,此时△>0 ∴
,此时△>0 ∴![]()
∴所求Q的坐标为(![]() ,0)………………………………13分
,0)………………………………13分
解法二:由题意知直线l的斜率k存在且不等于零
设l的方程:![]() ,A(
,A(![]() ),B(
),B(![]() ),则Q(
),则Q(![]() ,0)
,0)
∵![]() ∴Q分
∴Q分![]() 的比为
的比为![]()
由定比分点坐标公式得: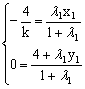
即得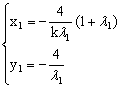 下同解法一……………………………………13分
下同解法一……………………………………13分
解法三:由题意知直线l的斜率k存在且不等于零
设l的方程:![]() ,A(
,A(![]() ),B(
),B(![]() ),则Q(
),则Q(![]() )
)
∵![]()
∴![]()
∴![]()
∴![]()
又![]()
∴![]() 即
即![]()
将![]() 得:
得:![]()
∵![]() ,否则l与渐近线平行
,否则l与渐近线平行
∴![]()
∴![]() ∴
∴![]()
∴Q(![]() ,0)……………………………………13分
,0)……………………………………13分
解法四:由题意知直线l的斜率k存在且不等于零
设l的方程:![]()
∵![]() ∴
∴![]()
∴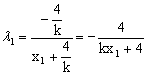
同理![]()
即![]()
又由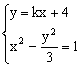 消去y,得
消去y,得![]()
当![]() 时,则直线l与双曲线的渐近线平行,不合题意,
时,则直线l与双曲线的渐近线平行,不合题意,![]()
由韦达定理有: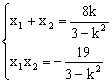
代入(*)式得![]()
∴所求Q点的坐标为(![]() ,0)……………………………………13分
,0)……………………………………13分
20. (本题满分13分)
解:(1)令m=n=1,由![]() ,得
,得![]()
∴f(1)=0………………………………………………………………3分
(2)∵f(2)=1,∴![]()
又f(x)在(0,![]() )上单调递增
)上单调递增
∴0<x<4 ∴f(x)<2的解集为(0,4)……………………7分
(3)∵f(1)=0,f(x)在(0,![]() )上单调递增
)上单调递增
∴![]() 时,f(x)<0
时,f(x)<0
![]() 时,f(x)>0
时,f(x)>0
又![]()
∴f(a)=f(b)或![]()
∵0<a<b ∴![]()
∴![]()
∴ab=1 ∴0<a<1<b
又∵![]() ,且b>1,
,且b>1,![]()
∴![]() ,∴
,∴![]()
∴![]() ,考虑到0<a<1
,考虑到0<a<1
∴![]()
∴![]() …………………………………………13分
…………………………………………13分