黑龙江省西北部重点中学2007年高三第二次模拟考试
数学理科
本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，满分150分，考试用时120分钟。
第Ⅰ卷 (选择题，共60分)
一、选择题：本大题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题意要求的.
1.已知
，则
的值为（
）
A
．
B．
C．
D． 
2.若复数
的平方是纯虚数，则（
）
A．
B．
C．
D．
3.若半径为1的球面上两点A，B间的球面距离为
，则弦长AB等于（ ）
A．
B．1
C．
D．
4.函数
在
上的图像与
轴的交点的横坐标为（
）
A．
B．
C．
D．
5.函数
与
的图像关于直线
对称，则下列结论错误的是（
）
A．
B．
C．
D．
6.一个等差数列的前4项是
，，
，
，则
等于（
）
A．
B．
C．
D．
7.已知点P
在不等式组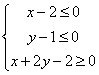
表示的平面区域上运动，则
的取值
范围是（ ）
A．[－2，－1] B．[－2，1] C．[－1，2] D．[1，2]
8.在正方体ABCD－A1B1C1D1中，直线A1B与平面ABC1D1所成的角为（ ）
A．
B．
C．
D．
9.设两直线x+2y+1=0，2x+y+1=0的倾斜角分别为α、β，则α+β等于（ ）
A．60。 B．90。 C．270。 D．300。
10.设s，t是非零实数，i、j是单位向量，当两向量si+tj，ti－sj的模相等时，i与j的夹角是（ ）
A．
B．
C．
D．
11.双曲线
的虚轴端点与一个焦点连线的中点在与此焦点对应的准线上，
是双曲线的一条垂直于实轴的弦，
为坐标原点。则
等于（
）
A．0
B．
C．
D．
12.已知集合
，且
，
则整数对（a, b）的个数为（ ）
A. 20 B. 25 C. 30 D. 42
第II卷（非选择题，共90分）
二、填空题（本题满分16分，每小题4分，共4个小题。请将答案直接填入题后的横线中）
13.
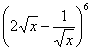的展开式的中间项为
。
14.函数
的单调递增区间是
。
15. 函数
图像的对称中心的坐标为
。
16. 已知椭圆
的左右焦点分别为F1与F2，点P在直线l：
上，
当
取最大值时，点P的坐标为
。
三、解答题（本大题共6个小题，共74分。解答应写出文字说明，推证步骤或演算过程）
17、（本小题满分12分）已知函数
为偶函数，且其
图像上相邻的一个最高点和最低点之间的距离为
。
（1）求函数f(x)的解析式；
（2）若
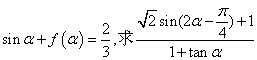的值。
18、（本小题满分12分）一块集成电路板上有16个焊点，其中有两个不合格的“坏”焊点，其余的都是合格的“好”焊点。现要对16个焊点逐个进行检查，直到这两个“坏”焊点都被查出为止。设ξ是检查出两个“坏”焊点时已检查焊点的个数。
（1）求ξ的分布列；
（2）求检查焊点不超过8个就检查出两个“坏”焊点的概率；
（3）平均要检查多少个焊点就可能将这两个“坏”焊点都找出？
19、（本小题满分12分）已知点列
，且
与
向量
共线，n是正整数，O是坐标原点，设x1=1.
（1）求 x2, x3 ;
（2）求数列{xn}的通项公式。
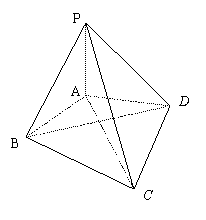
20、（本小题满分12分）如图所示，在四棱锥P—ABCD中，PA⊥底面ABCD，
∠ABC=∠ADC=90°，∠BAD=120°， AD = AB = a, 若PA = λa（λ＞0）。
（1）求证：平面PBD⊥平面PAC；
（2）当
时，求点A到平面PDC的距离；
（3）当λ为何值时，点A在平面PBD的射影恰好是△PBD的重心。
21、（本小题满分12分）已知函数
在区间（1，2 ]上是增函数，
在区间（0，1）上为减函数。
（1）试求函数
的解析式；
（2）求证：当
x >0时，方程
有唯一解。
22、（本小题满分14分）椭圆的中心在原点O，它的短轴长为
，相应于
焦点F（c，0）的准线l与x轴相交于点A，OF = 2FA，过点A的直线与椭圆相交
于P、Q两点。
（1）求椭圆的方程；
（2）若
，求直线PQ的方程；
（3）设
，过点P且平行于准线l的直线与椭圆相交于另一点M，
求证：
.
黑龙江省西北部重点中学2007年高三第二次模拟考试
数学理科参考答案
一、选择题：（共12小题，每小题5分，共60分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 选项 | A | B |
|
|
|
|
|
|
| A |
| C |
二、填空题：（共4小题，每小题４分，共16分）
13．－160 14．
15．
16．（-10，-4）或（-2，4）
17、解：
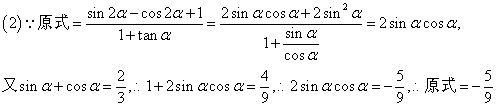
18、（理）解：（1）
列表写出（略）
（2）
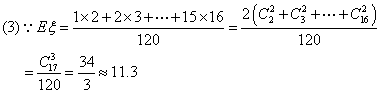
故平均要检查焊点11个到12个，就可以检查出两个“坏”焊点。
20、（2）
（3）
21、解：
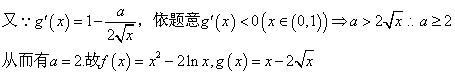
（2）由（1）可知，原方程为
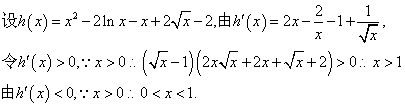
所以，h(x)在(0,1)上是减函数；在（1，+∞）上是增函数。
即h(x)在x=1处有一个最小值0，即当x>0且x≠1时h(x)
> 0 ，所以h(x)=0只有一个实数解。故当 x >0时，方程有唯一解。
