|
东北师大附中
辽宁省实验中学
数学试卷(文)
第Ⅰ卷(选择题,共60分)
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知集合![]() ,那么
,那么![]() 等于 ( )
等于 ( )
A. ![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.在等比数列![]() 中,已知
中,已知![]() ,那么
,那么![]() 等于 ( )
等于 ( )
A.4 B.6 C.12 D.16
3.已知单位向量![]() 的夹角为
的夹角为![]() ,那么∣
,那么∣![]() ∣等于 ( )
∣等于 ( )
A.![]() B.3
C.
B.3
C.![]() D.
D.![]()
4.![]() 的反函数是 ( )
的反函数是 ( )
A.![]() B.
B.![]()
C.![]() D.
D. ![]()
5.![]() 表示平面,
表示平面,![]() 表示直线,则
表示直线,则![]() 的一个充分不必要条件是 ( )
的一个充分不必要条件是 ( )
A.![]() B.
B.![]() 且
且![]()
C.![]() D.
D. ![]()
6.由5学生组成两个调查小组进行社会实践,其中甲、乙两人必须在同一组的分组个数共有 ( )
A.4 B.5 C.6 D.7
7.已知抛物线![]() ,直线l过焦点F且与x轴不重合,则抛物线被l垂直平分的弦共有 ( )
,直线l过焦点F且与x轴不重合,则抛物线被l垂直平分的弦共有 ( )
A.不存在 B.有且只有1条 C.2条 D.3条
8.长方体的对角线长度是![]() ,若长方体的8个顶点都在同一个球面上,则这个球的表面积是 ( )
,若长方体的8个顶点都在同一个球面上,则这个球的表面积是 ( )
A.![]() B.
B. ![]() C.
C.![]() D.
D.![]()
9.在![]() 的展开式中,
的展开式中,![]() 的系数是 ( )
的系数是 ( )
A.-55 B.45 C. -25 D.25
|
A.![]() B.
B.![]() C.
C. ![]() D.
D.![]()
11.已知![]() 的三个内角A、B、C所对的三边分别为a、b、c,若
的三个内角A、B、C所对的三边分别为a、b、c,若![]() 的面积
的面积![]() ,则
,则![]() 等于 ( )
等于 ( )
A.![]() B.
B.![]() C.
C.![]() D.1
D.1
12.函数![]() 在区间
在区间![]() 上有最小值-2,则实数a的值为 ( )
上有最小值-2,则实数a的值为 ( )
A.2
B.![]() C.-2 D.4
C.-2 D.4
第Ⅱ卷(非选择题,共90分)
二、填空题:本大题共4小题,每小题4分,共16分.
13.某校高三年级有1200人,某次考试中成绩为A等第的有120人,B等第的有840人,C等第的有240人.为了了解考试情况,从中抽取一个容量为200的样本,若采用分层抽样方法,其中C等第的的抽取人数是 人.
14.等差数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() __________.
__________.
15.直线![]() 过双曲线
过双曲线![]() 的右焦点
的右焦点![]() ,方向向量为
,方向向量为![]()
![]() ,若原点到直线
,若原点到直线![]() 的距离是原点到右准线距离的
的距离是原点到右准线距离的![]() 倍,则双曲线的离心率为_______.
倍,则双曲线的离心率为_______.
|
三、解答题:本大题共6小题,共74分.解答应写出必要的文字说明、证明过程或演算步骤
17.已知![]() ,
,![]() 。
。
记![]() ,并且
,并且![]() 的最小正周期为
的最小正周期为![]() 。
。
(1)求![]() 的最大值及取得最大值的
的最大值及取得最大值的![]() 的集合。
的集合。
(2)将函数![]() 的图象按向量
的图象按向量![]() 平移后得函数
平移后得函数![]() 的图象,求
的图象,求![]() 的最小值
的最小值
18.(本小题满分12分)
甲、乙两人射击,每次射击是相互独立事件,规则如下:若某人一次击中,则继续射击;若一次不中,就由对方接替射击。已知甲、乙二人每次击中的概率均为![]() ,若两人合计共射击3次,且第一次由甲开始射击。求:
,若两人合计共射击3次,且第一次由甲开始射击。求:
(1)甲击中3次的概率;
(2)甲恰好击中1次的概率.
|
(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的正切值。
的正切值。
|
20.已知函数![]() .
.
(1) 若函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,求实数
上单调递增,求实数![]() 的值;
的值;
(2) 求证:当![]() 时,
时,![]() 在
在![]() 上单调递减.
上单调递减.
21.已知等比数列![]() 共有
共有![]() 项(
项(![]() ,且各项均为正数,
,且各项均为正数,![]() ,
,![]() ,
,
(1)求数列![]() 的通项;
的通项;
(2)若数列![]() 是等差数列,且
是等差数列,且![]() ,判断数列
,判断数列![]() 的前
的前![]() 项和
项和![]() 与数列
与数列![]() 的前
的前![]() 项的和
项的和![]() 的大小,并加以证明。
的大小,并加以证明。
22.过双曲线![]() 的上支上一点
的上支上一点![]() 作双曲线的切线交两条渐近线分别于点
作双曲线的切线交两条渐近线分别于点![]() .
.
(1) 求证:![]() 为定值;
为定值;
(2) 若![]() ,求动点
,求动点![]() 的轨迹方程.
的轨迹方程.
|
东北师大附中
辽宁省实验中学
数学试卷(文)参考答案
一.选择题
1.B 2.A 3.C 4.B 5.D 6.D 7.A
|
二.填空题
13.140; 14.12; 15.![]() 16.②⑥
16.②⑥
三.解答题
17. (本小题满分12分)
解:(1)![]()
因为最小正周期为![]() ,
,![]()
所以 ![]() ,
,
易知![]() , 即
, 即![]() 。
。
(2)![]()
![]()
![]()

18.解:(1)记“甲同学恰好击中2次”为事件A,则![]()
(2)记“甲恰好击中1次”为事件B,则![]()
答:甲击中3次的概率为![]() ,甲恰击中1次的概率为
,甲恰击中1次的概率为![]()
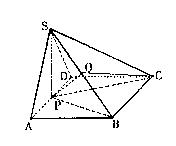
19解:(1)因为面SAD⊥面ABCD,面SAD∩面ABCD=AD,
SP⊥AD,SP![]() 面SAD 所以SP⊥面ABCD
面SAD 所以SP⊥面ABCD
所以SP⊥BC
又∠DAB=60o 所以PB⊥BC
且PB∩SP=P 所以BC⊥平面SPB
 20解:
20解:
(1)![]() ,
,
![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,说明
上单调递增,说明![]() 是函数
是函数![]() 的极值点
的极值点
![]() ,解得
,解得 ![]() .
.
(2) 证明:若使![]() 在
在![]() 上单调递减,则对
上单调递减,则对![]() 恒有
恒有![]() .
.
![]() ,其对称轴为
,其对称轴为 ![]() .
.
当![]() 时,
时,![]() ,即
,即 ![]() ,
,
则![]() 在
在![]() 上的最大值为
上的最大值为![]() 或
或![]() .
.
![]() 当
当![]() 时,
时,![]() ,
,![]() ,
,
![]() 对
对![]() ,恒有
,恒有![]() ,即当当
,即当当![]() 时,
时,![]() 在
在![]() 上单调递减.
上单调递减.
21.解:(1)设等比数列![]() 的公比为
的公比为![]() ,则
,则![]() 由
由![]() 的各项都是正数,得
的各项都是正数,得![]() ,所以
,所以![]() 。
。
(2)由![]() 得
得![]() ,又数列
,又数列![]() 是等差数列,且
是等差数列,且![]()
![]()
![]() ,
,![]() ,
,
所以当![]() 取3时,
取3时,![]() ,此时
,此时![]() ,当
,当![]() 。
。
22.解:(1)设直线AB:![]()
由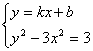 得
得![]()

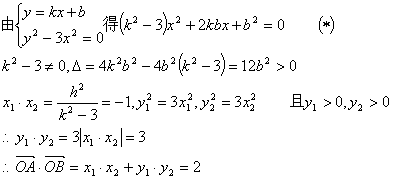
(2)![]() ,所以四边形BOAM是平行四边形
,所以四边形BOAM是平行四边形
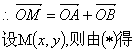
![]() ①
①
![]() ②
②
由①②及![]()
![]()
另解:设![]() ,则
,则![]() ,
,
由![]() 求导得
求导得![]()
![]()
![]()
![]() 切线方程为
切线方程为![]() 即
即![]()
![]()
![]()
![]()
![]()
设切线与![]() 交于
交于![]() ,与
,与![]() 交于
交于![]()
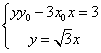 得
得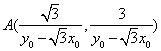
![]()
![]()
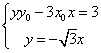 得
得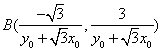
![]()
![]()
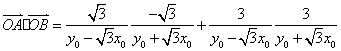
![]() =
=![]() =
=![]() =2
=2
![]()
![]()
(2)设![]() ,
,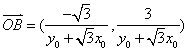
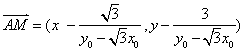
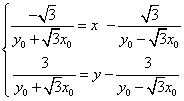
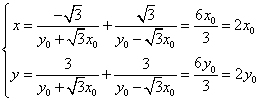
![]()
![]()
![]()
![]()
![]()
又![]()
![]()