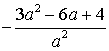枣庄市2007届高三模拟考试
文科数学试题(一)
本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试时间120分钟.
第Ⅰ卷(选择题,共60分)
注意事项:
1. 答案第Ⅰ卷前,考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上.
2. 每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案,不能答在试题卷上.
3. 考试结束、监考人将本试卷和答题卡一并收回.
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,选择一个符合题目要求的选项.
1. 已知命题![]() ,
,![]() ,则非
,则非![]() 是( )
是( )
![]() .
.![]() ,
,![]()
![]() .
.![]() ,
,![]()
![]() .
.![]() ,
,![]()
![]() .
.![]() ,
,![]()
2.设复数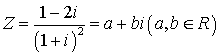 ,那么点
,那么点![]() 在第( )象限
在第( )象限
A.一 B.二 C.三 D.四
3.在![]() 中,
中,![]() 分别是角
分别是角![]() 所对的边,则
所对的边,则
“![]() ”是“
”是“![]() 成等差数列”的( )
成等差数列”的( )
A.充分条件 B.必要条件 C.充要条件 D.既不必要也不充分
4.已知![]() 是两个不同的平面,
是两个不同的平面,![]() 是两条不同的直线,则下列命题不正确的是( )
是两条不同的直线,则下列命题不正确的是( )
A.若![]() ,
,![]() ,则
,则![]() B.若
B.若![]() ,
,![]() 则
则![]()
C.若![]() ,
,![]() ,
,![]() ,则
,则![]()
D.若![]() ,
,![]() ,则
,则![]()
5.已知非零向量![]() 与
与![]() 满足
满足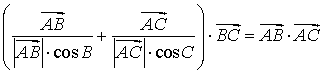 ,则
,则![]() 为( )
为( )
A.三边均不等的三角形 B.直角三角形 C.等腰非等边三角形 D.等边三角形
6.从1,2,…,9这九个数中,随机抽取2个不同的数,则这2个数的和为偶数的概率是( )
![]() .
.![]()
![]() .
.![]()
![]() .
.![]()
![]() .
.![]()
7.各项都是正数的等比数列![]() 的公比
的公比![]() 且
且![]() 则
则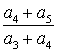 的值为( )
的值为( )
![]() .
.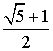 或
或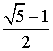
![]() .
.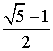
![]() .
.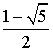
![]() .
.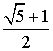
8.某工厂生产一批产品,它们来自甲,乙,丙,丁四个车间,为检验这批产品的质量,决定采用分层抽样法,共抽取了160件.如果甲,乙,丙,丁四个车间抽取的个体数组成一个公差为20的等差数列,且已知乙车间生产了1200件产品,则这批产品共有( )件.
![]() .2400
.2400 ![]() .4800
.4800 ![]() .6400
.6400 ![]() .3600
.3600
9.直线![]() 与圆
与圆![]() 交于
交于![]() 两点,则
两点,则![]() (
(![]() 为圆心)的面积等于( )
为圆心)的面积等于( )
![]() .
.![]()
![]() .
.![]()
![]() .
.![]()
![]() .
.![]()
10.两个人约定在晚上8点到9点之间在某处见面,并约定先到者应等候15分钟,过时就离去,则两人能会面的概率为( )
![]() .
.![]()
![]() .
.![]()
![]() .
.![]()
![]() .
.![]()
11.已知函数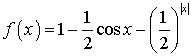 ,下列说法正确的是( )
,下列说法正确的是( )
![]() .
.![]() 为奇函数,且
为奇函数,且![]() 的最大值为
的最大值为![]()
![]() .
.![]() 为奇函数,且
为奇函数,且![]() 的最小值为
的最小值为![]()
![]() .
.![]() 为偶函数,且
为偶函数,且![]() 的最大值为
的最大值为![]()
![]() .
.![]() 为偶函数,且
为偶函数,且![]() 的最小值为
的最小值为![]() ;
;
12.已知实系数方程![]() 的两根分别为一个椭圆和一个双曲线的离心率,则
的两根分别为一个椭圆和一个双曲线的离心率,则![]() 的取值范围是( )
的取值范围是( )
![]() .
.![]()
![]() .
.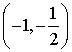
![]() .
.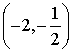
![]() .
.![]()
| |
二、填空题:本大题有4小题,每小题4分,共16分. 把答案填在题中横线上.
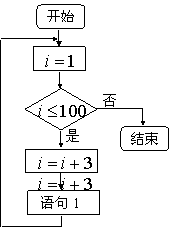 |
13.下列流程图中,语句1将被执行的次数为________.
14.抛物线![]() 与直线
与直线![]() 交于
交于
两点![]() ,设抛物线的焦点为
,设抛物线的焦点为![]() ,
,
则![]() =_____________________.
=_____________________.
15.已知![]() 在
在![]() 上是单调函数,
上是单调函数,
则![]() 的取值范围是___________.
的取值范围是___________.
16.在直角三角形中,若两条直角边长分别为![]() ,则此三角形外接圆的半径是
,则此三角形外接圆的半径是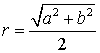 .把此结论类比到空间为_________________________________________.
.把此结论类比到空间为_________________________________________.
三、解答题:本大题有6小题,共74分. 解答应写出文字说明,证明过程或演算步骤.
17.已知向量![]() ,
,![]() ,
,![]() .
.
(1)若![]() ,求
,求![]() 的值;(2)若
的值;(2)若![]() ,求函数
,求函数![]() 的值域.
的值域.
18.把一个骰子投掷2次,观察出现的点数,并记第一次出现的点数为![]() ,第二次出现的点数为
,第二次出现的点数为![]() ,试就方程组
,试就方程组![]() 解决下列问题:
解决下列问题:
(1)求方程组只有一组解的概率;(2)求方程组只有正整数解的概率.
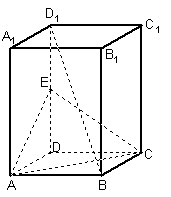
19.已知一个多面体的直观图及三视图如图所示,点![]() 在棱
在棱![]() 上,截面
上,截面![]() ,二面角
,二面角![]() 的大小为
的大小为![]() .
.
(1)求证:点![]() 为棱
为棱![]() 的中点;
的中点;
(2)求证:![]() ;
;
 (3)设
(3)设![]() 与
与![]() 的交点为
的交点为![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
 |
20.设函数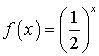 ,数列
,数列![]() 满足
满足![]() ,
,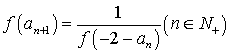
(1)求![]() 的表达式;
的表达式;
(2)令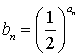 ,
,![]() ,
,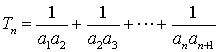 ,求
,求![]() 及
及![]() 的表达式;
的表达式;
(3)在(Ⅱ)的条件下,设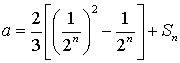 ,
,![]() ,试比较
,试比较![]() 与
与![]() 的大小(不需要证明).
的大小(不需要证明).
21.椭圆![]() 的中心在原点
的中心在原点![]() ,它的短轴长为
,它的短轴长为![]() ,右焦点为
,右焦点为![]() ,且
,且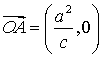 ,
,![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过椭圆![]() 的左焦点
的左焦点![]() 任作一条与两坐标轴都不垂直的弦
任作一条与两坐标轴都不垂直的弦![]() ,在
,在![]() 轴上是否存在点
轴上是否存在点![]() ,使直线
,使直线![]() 与直线
与直线![]() 关于
关于![]() 轴对称,若存在,求出点
轴对称,若存在,求出点![]() 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.
22.已知函数![]() ,以
,以![]() 为切点的切线的倾斜角为
为切点的切线的倾斜角为![]() .
.
(1)求![]() 的值;
的值;
(2)求使得不等式![]() 对于
对于![]() 恒成立的最小正整数
恒成立的最小正整数![]() 的值;
的值;
(3)若![]() ,求
,求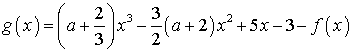 的单调区间,并确定零点的个数.
的单调区间,并确定零点的个数.
枣庄市2007届高三模拟考试
文科数学试题(一)参考答案及评分标准
一、选择题(每小题5分,共60分)BCCDB A DCAC DA
二、填空题(每小题4分,共16分)13.34 14.7 15.![]()
16.在空间三条侧棱互相垂直的四面体中,若三条侧棱长分别为![]() ,则此三棱锥外接球的半径为
,则此三棱锥外接球的半径为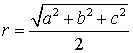
三、解答题
17.(1)![]() ,
,
![]() ,……………………………………………………………2分
,……………………………………………………………2分
即![]()
又![]()
![]() ……………………………………………… ……………………………4分
……………………………………………… ……………………………4分
![]() ………………………… …………………………… 6分
………………………… …………………………… 6分
(2)![]()
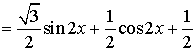
![]() . …………………………………………………………8 分
. …………………………………………………………8 分
![]() ,
, ![]() ,
,
![]() ,
,
![]() .…………………………………… ……………………………12 分
.…………………………………… ……………………………12 分
18.解:将骰子抛掷2次,共有6×6=36种等可能结果.…………………………2分
(1)当![]() 时,方程组只有一组解;
时,方程组只有一组解;
若![]() ,共有
,共有![]() 三种结果.
三种结果.
所以不满足![]() 的解有33组.
的解有33组.
所求概率![]() …………………………………………………………8分
…………………………………………………………8分
(2)若方程组只有正整数解,则![]()
于是,![]() 所以方程组只有正整数解为不可能事件.所求概率为0.……12分
所以方程组只有正整数解为不可能事件.所求概率为0.……12分
19.解:由图可知,此多面体是底面为正方形的直棱柱.
(1)连![]() ,设交点为
,设交点为![]() ,连
,连![]() ,
,
![]() 面
面![]() ,面
,面![]() 面
面![]() ,
,
![]()
![]() 为
为![]() 的中点,
的中点,
![]() 为
为![]() 的中点.……………………………………………………………4分
的中点.……………………………………………………………4分
(2)![]() 为正方形,
为正方形,
![]() .
.
![]() 面
面![]() ,
,
![]() ,
,
![]() 面
面![]() ,
,
![]() .………………………………………………………………… 8分
.………………………………………………………………… 8分
(3)![]() 面
面![]() ,
,
![]() ,
,![]() ,
,
![]() 就是二面角
就是二面角![]() 的平面角,即
的平面角,即![]() .
.
![]() ,
, 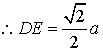 ,
, ![]() ,
, ![]() ,
,
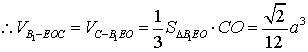 .……………………12分
.……………………12分
20. 解:(1)![]()
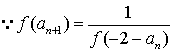
![]() 是首项为1,公差为2的等差数列,
是首项为1,公差为2的等差数列,
![]() .……………………………………………………………………………4 分
.……………………………………………………………………………4 分
(2)![]()
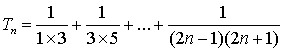
![]()
![]() ………………………………………… …………………………… 9分
………………………………………… …………………………… 9分
(Ⅲ)![]()
当![]() 时,
时,![]() .
.
当![]() 时,
时,![]() .…………………………………………………………………12 分
.…………………………………………………………………12 分
21.解:(1)由题意设椭圆![]() 的方程为
的方程为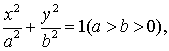
则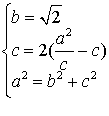 ,解得
,解得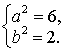
![]() 椭圆C的方程为
椭圆C的方程为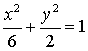 .………………………………………………… 4分
.………………………………………………… 4分
(2)假设存在点![]() ,又设直线
,又设直线![]()
代入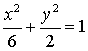 ,得
,得![]() .…………………………………… 6分
.…………………………………… 6分
设![]() ,则
,则
![]()
![]() 直线
直线![]() 与直线
与直线![]() 关于
关于![]() 轴对称.
轴对称.
![]() ………………………………………………………………… 8分
………………………………………………………………… 8分
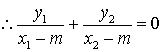 ,
,
即![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 存在点
存在点![]() ,使直线
,使直线![]() 与直线
与直线![]() 关于
关于![]() 轴对称.………………12 分
轴对称.………………12 分
22 .解:(1)![]() 则由题意知,
则由题意知,
![]() 即
即![]()
![]()
![]()
将![]() 代入
代入![]() 得:
得:![]() …………………………………………………3 分
…………………………………………………3 分
(2)令![]() 得:
得: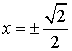
当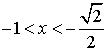 时,
时,![]()
当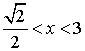 时,
时,![]()
又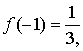
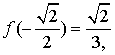
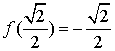
![]()
![]() 当
当![]() 时,
时,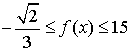 ………… ……………………………6分
………… ……………………………6分
要使![]() 对于
对于![]() 恒成立,
恒成立,
则![]() ,
, ![]()
![]() ………………………………………………………………………7分
………………………………………………………………………7分
(3)![]()
![]() ………………………8 分
………………………8 分
当![]() 时,
时,![]()
![]() 的增区间为
的增区间为![]()
![]()
![]() 在
在![]() 上有一个零点.
上有一个零点.
又![]() 在
在![]() 上为增函数.
上为增函数.
![]() 在
在![]() 上只有一个零点. …………………………………………………10 分
上只有一个零点. …………………………………………………10 分
当![]() 时,令
时,令![]() 则
则![]() 或
或![]() .
.
|
|
|
|
| 1 |
|
|
|
| 0 |
| 0 |
|
|
|
|
|
|
|
|
![]() 的增区间为
的增区间为![]() ;
;
![]() 的减区间为
的减区间为![]() . …………………………………………………………………12分
. …………………………………………………………………12分
![]() ,
,
![]() ,
,
![]() 在
在![]() 内有一个零点.
内有一个零点.
又由![]() 的单调性及
的单调性及![]() 知,
知,
![]() 在
在![]() 上有且只有一个零点 . …………………………………………………14分
上有且只有一个零点 . …………………………………………………14分