枣庄市2007届高三模拟考试
文科数学试题(三)
本试卷分为第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共150分，考试时间120分钟.
第Ⅰ卷（选择题，共60分）
注意事项：
1． 答案第Ⅰ卷前，考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上.
2． 每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案，不能答在试题卷上.
3． 考试结束、监考人将本试卷和答题卡一并收回.
1.设全集为
，若集合
，
，则
等于（ ）
. 
. 
. 
. 
2．i是虚数单位，复数
等于（ ）
.－1－i .-1+ i .1- i .1+i
3.若等差数列
的公差
，且
，
，则数列的通项公式是（ ）
. 
. 
. 
. 
4、下列命题中假命题为（ ）
. 空间中过直线外一点有且仅有一条直线与该直线垂直
.仅存在一个实数
,使得
成等比数列
.存在实数
、
满足
,使得
的最小值是6
.
恒成立
5.在
中，
，则的形状为
. 直角三角形
. 等腰三角形或直角三角形
. 等腰直角三角形
. 正三角形
6.已知两条不同直线
与平面
，则下列结论正确的是 （ ）
. 
. 
. 
. 
7.直线
与圆
交于
两点，则的面积等于
（ ）
. 
. 
. 
. 
8.平面向量
，若
，则这样的向量
有
（ ）
. 
. 
. 
. 
9. 抛物线y＝4x2上的一点M到焦点的距离为1，则点M的纵坐标是（ ）
A．
B．
C．
D．1
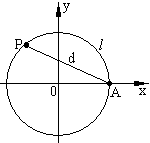
10. 如图, 设点A是单位圆上的一定点, 动点P从点A出
发在圆上按逆时针方向旋转一周, 点P所旋转过的弧
的长为l, 弦AP的长为d, 则函数
的图象
大致是( )．
11.
设
是曲线
上的点，若
,则（ ）
. 
. 
. 
. 
12. 北京市为成功举办2008年奥运会，决定从2003年到2007年五年间更新市内现有的全部出租车，若每年更新的车辆数比前一年递增10%，则2003年底更新现有总车辆数的(参考数据：1.14=1．46，1.15=1．61) （ ）
.10% . 16．4% .16．8% .20%
| |
二、填空题：本大题有4小题，每小题4分，共16分. 把答案填在题中横线上.
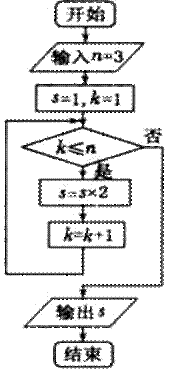13．右图所示的程序框图的输出结果为 ．
14．已知直线
过点
，且与
轴、
轴的正半轴分别交于
两点，
为坐标原点，则三角形
面积的最小值为 ．
15.已知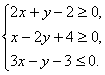
则s＝x2＋y2的最大值是___________．
16.设函数
的定义域为D，如果对于任意的
，
存在唯一的
，使
（C为常数）成立，则称函数在D上均值为C.给出下列四个函数：
①
②
③
④y=2x
则满足在其定义域上均值为2的所有函数的序号是 .
三、解答题：本大题共6小题，共74分，解答应写出文字说明，证明过程或演算步骤．
17．（本小题满分12分）
已知A、B、C是△ABC的三个内角，a，b，c为其对应边，向量
，且
.
（1）求角A；
（2）若
求△
的面积S．
18 . (本小题满分12分)
已知数列{
}是首项为且公比
不等于1的等比数列，
是其前n项的和，
成等差数列.
（1）证明: 
成等比数列；
（2）求
.
19．（本小题满分12分）
连续掷两次骰子,以先后得到的点数
、
为点P（,）的坐标，设圆Q的方程为
.
（1）求点P在圆Q上的概率；
（2）求点P在圆Q外部的概率.
20．（本小题满分12分）
如图，在三棱锥P-ABC中，PA⊥底面ABC，△ABC为正三角形，D、E分别是BC、CA的中点.
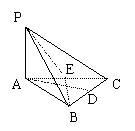(1)证明：平面PBE⊥平面PAC；
(2)如何在BC上找一点F，使AD//平面PEF？并说明理由；
(3)若PA=AB=2，对于(2)中的点F，求三棱锥B-PEF的体积.
21．（本小题满分12分）
直角梯形ABCD中∠DAB＝90°，AD∥BC，AB＝2，AD＝
，
BC＝
．椭圆C以A、B为焦点且经过点D．
（1）建立适当坐标系，求椭圆C的方程；
（2）若点E满足
，问是否存在不平行AB的直线l与椭圆C交于M、N两点，且
，若存在，求出直线l与AB夹角的范围，若不存在，说明理由．
22．已知函数=
.
（1）当
时,求的极小值;
（2）当
时, y＝的零点个数.
枣庄市2007届高三模拟考试
文科数学试题(三)参考答案及评分标准
一、选择题（每小题5分，共60分）BBDAA DABBC AB
二、填空题（每小题4分，共16分）13.8 ; 14.4 ; 15.13 ; 16. ①③.
三、解答题：
17．（1）∵
，∴
……………………………………2分
∴sin（A－
）＝ .…………………………………………………………3分
∵0<A<π，∴－<A－<
π ，………………………………………………4分
∴A－＝．
∴A＝
…………………………………………………………………………5分
（2）∵
∴由正弦定理，得
…………………………7分
∴cosBsinC－sinBcosC＝0，即sin（B－C）＝0．……………………………9分
∵B、C为△ABC的内角，∴B＝C．
又A＝
，∴B＝C＝
∴△ABC为正三角形．……………………………10分
又
，∴S＝
…………………………12分
18．（1）证明： 由
成等差数列，
得 
，
即 
变形得 
所以
（舍去）.…………………………………………………… 3分
由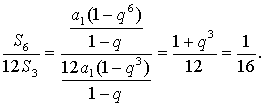 
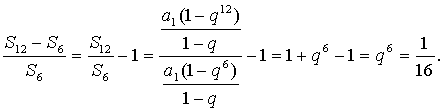
得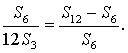 
所以12S3，S6，S12－S6成等比数列.…………………………………………………… 6分
（2）解：
即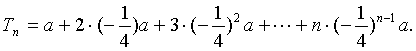 
①
①×
得： 
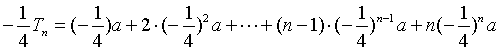.②
①－②有：
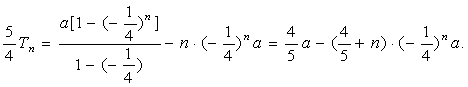
所以，
……………………………………12分
19.解：连续掷两次骰子, 的所有可能值为1，2，3，4，5，6；的所有可能值为1，2，3，4，5，6,所以点P（、）的所有可能情况有36种，且每一种情况的出现是等可能的，因此本问题属古典概型问题. ……………………………………………………………… 4分
（1）点P在圆Q上的点只有
两种情况,根据古典概型公式，点P在圆Q上的概率为
；……………………………………………………………………8分
（2）点P在圆Q内部的点是（1，1）、（1，2）、（1，3）、（2，1）、（2，2）、（2，3）、（3，1）、（3，2），共有8个点，所以点P在圆Q外部的概率为
=
. ………12分
20.解：(1) ∵PA⊥底面ABC，∴PA⊥BE.
又∵△ABC是正三角形，且E为AC的中点，∴BE⊥CA.
又
，∴BE⊥平面PAC.
∵BE
平面PBE，∴平面PBE⊥平面PAC.………………………………………………… 4分
(2)取CD的中点F，则点F即为所求.
∵E、F分别为CA、CD的中点，∴EF//AD.
又EF平面PEF，AD
平面PEF，∴AD//平面PEF.……………………………………… 8分
(3)
.
………………………12分
21.讲解：（1）如图，以AB所在直线为x轴，AB中垂线为y轴建立直角坐标系， A（-1，0），B（1，0）
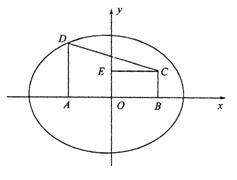
设椭圆方程为：
，
① 又
②
由①②可得
∴ 椭圆C的方程是：
…………………………………………………4分
（2）
，
，l⊥AB时不符合题意.…………………………5分
设l：y＝kx＋m（k≠0）,
由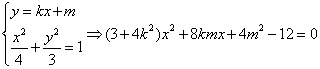 
,…………………………7分
M、N存在
.
设M（
，
），N（
，
），MN的中点F（
，
），
∴ 
，
.…………………………9分
∴
∴
∴
, ∴
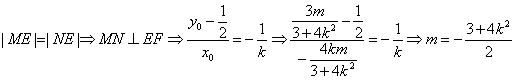
且
∴ l与AB的夹角的范围是
，
．………………………………………………12分
22.解: （1） ∵=, ∴ 
=
.………………………………………2分
当时,
<1,
∴当x<或x>1时, >0;当<x<1时<0.……………………………… 4分
∴当x=1时,的极小值为
; …………………………………………6分
（2）当a=0时,=
,y＝只有一个零点x=1;…………………………7分
若0<a<2, 则>1, 当x<1或x>时, >0;当1<x<时<0.
∴ 的极大值为 <0.
∴y＝的图像与x轴只有一个交点,函数只有一个零点;………………
9分
若a=2,则=
,函数y＝单调递增,
∴y＝的图像与x轴只有一个交点,函数只有一个零点;………………
11分
若a>2,由（1）知的极大值为
;
∴y＝的图像与x轴只有一个交点,函数只有一个零点;………………
13分
综上所述,时, y＝零点只有一个.……………………………………… 14分