枣庄市2007届高三模拟考试
文科数学试题(二)
本试卷分为第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共150分，考试时间120分钟.
第Ⅰ卷（选择题，共60分）
注意事项：
1． 答第Ⅰ卷前，考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上.
2． 每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案，不能答在试题卷上.
3． 考试结束、监考人将本试卷和答题卡一并收回.
一、选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，选择一个符合题目要求的选项.
1.若集合
，则
表示的图形面积为
A．
B．
C．
D．
2.抛掷两个骰子，至少出现一个5点或6点的概率为
A．
B．
C．
D． 
3.设直线过点
，斜率为1，且与圆
相切，则
的值为
A．
B．
C．
D． 
4.已知等差数列
的第
项为
，第项为
，则数列
的通项公式
为
A．
B．
C．
D．
5.函数图象与轴虽有交点，但不宜用二分法求交点横坐标的是
 |  | ||||||
 | |||||||
 | |||||||
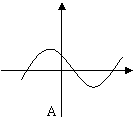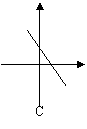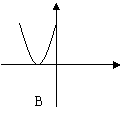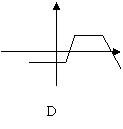6.已知函数
，则函数的最小正周期T和它图象上的一条对称轴方程是
A．
B．
C．
D．
7. O为空间中一定点，动点
在
三点确定的平面内且满足
，则点的轨迹一定过
的
A.外心 B.内心 C.重心 D.垂心
8.过正三棱锥
的侧棱
与底面中心
作截面
，已知截面是等腰三角形，则侧面与底面所成角的余弦值为
A.
B.
C.
D.
9.函数
的图象与函数
的图象关于原点对称，则
的表达式为
A．
B．
C．
D．
10.如果以原点为圆心的圆经过双曲线
的焦点，且与直线
交于
两点，且
，则双曲线的离心率为
A．
B．
C．
D．2
11.给出以下一个算法的程序框图如图所示，该程序框图的功能是
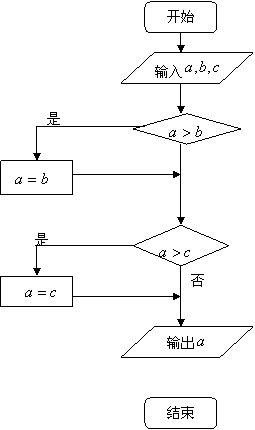A．求出
三数中的最大数
B．求出三数中的最小数
C．按按从小到大排序
D．将按从大到小排序
12.在下列四个函数中，满足性质：“对于区间
上的任意
恒成立”的只有
A．
B．
C．
D．
| |
二、填空题：本大题有4小题，每小题4分，共16分. 把答案填在题中横线上.
13.
是虚数单位，则复数
______.
14.采用系统抽样法，从121人中抽取一个容量为12的样本，则每个人被抽取的概率为_____.
15.设函数对一切实数
满足条件
，且方程
恰有6个不同实根，则这6个实根之和是_____.
16.已知
表示两条不同的直线，
表示三个平面，下列命题中：
①若
，且
，则
；
②若相交，且都在
外，
，则；
③若
；
④若
，其中正确命题的序号是___________.
三、解答题：本大题有6小题，共74分. 解答应写出文字说明，证明过程或演算步骤.
17.（12分）某市教育部门最近出台一项规定，全市每一位在职教师必须参加某项计算机及教育技能综合考试，每位教师一年之内最多有4次参加考试的机会，一旦某次考试获得60分以上则称通过了考试，可领取合格证书，不再参加以后的考试，否则就一直考到第4次为止.如果某教师参加考试通过的概率依次为0.5，0.75，0.8，0.9.
(1) 求某教师在一年内第二次就通过了考试的概率.
(2) 求某教师在一年内能领取合格证书的概率.
18.（12分）在中，
分别是角的对边，
，且
.
（1）求
的大小;
（2）求
取最大值时，A的大小.
19.（12分）已知数列的前
项和为
，且
，数列
中
，点
在直线
上.
（1）求数列
的通项;
（2）记
，求满足
的最大整数.
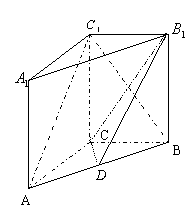20.（12分）如图，已知在侧棱垂直于底面三棱柱
中，
，点D是AB的中点.
（1）求证：
;
（2）求证：
;
（3）求三棱锥
的体积.
21.（12分）已知函数
，其中为实数，为参数，
要使函数的极小值大于零，求参数的取值范围；
22.（14分）已知点
，点为直线
图象上一点，且
（1）求点
的坐标;
（2）求以
为焦点且过点
的椭圆C的方程;
（3）已知点
，若E满足
，问是否存在直线
与椭圆交于
两点，且
？若存在，求出直线的斜率
的取值范围；若不存在，请说明理由.
枣庄市2007届高三模拟考试
文科数学试题(二)参考答案及评分标准
一、选择题（每小题5分，共60分）A D C A B C D C D B B A
二、填空题（每小题4分，共16分）13. 14.
15.
16.②③
17.解：（1）某教师在第二次就通过考试的概率为
……….6分
（2）某教师在一年内能领取合格证的概率为：
…………………………………….12分
18.解析：（1）由得
，从而
，
由正弦定理得
，
，
，
，
…….6分
（2）
，…………………………………………………………………………..9分
由（1）知，
，当
时，
………………………………………………………………………………………………….12分
19.解：（1）
，即
，
……………………3分
由在直线上得，
……………………………………………………6分
（2）
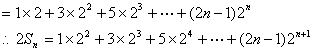
相减得
…………………………………………………………………9分
，由于当
时，
，当
时，
，所以. ………………………………………………………
12分
20.解：（1）在中，由余弦定理得
，
为直角三角形
1
，
，
………………………………………4分
（2）连接
交
于
，则为的中点，连接
，则在
中，
，又
，则 …………………………………………………..8分
（3）
(体积相减)………………………………………………………………..12分
21.解：（1）因为
所以
………………….3分
①当
时，
，则在
内是增函数，所以无极值………….5分
②当
时，
符号变化、变化如下
所以在
处取得极小值
.……………………………….9分
要使
，又，所以解得
.由上得，若函数的极小值大于0，
的取值范围是. …………………………………………………………….. 12分
22.解：（1）设H的坐标为
，则
解得
，因此，点的坐标为
…………………………………………. 3分
（2）
，根据椭圆定义，
得
，
所求椭圆方程为
……………………………………..7分
（1）
由得点的坐标为
.显然直线与轴平行时满足题意，即
.直线与轴垂直时不满足题意，不妨设直线
由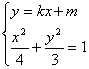
得
，
设
的中点为
，
则
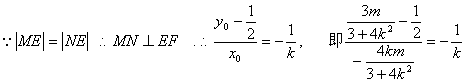
解得：
，由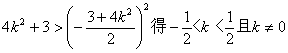
综上，直线的斜率值的取值范围是
………………………………………. 14分