枣庄市2007届高三模拟考试
理科数学试题(一)
本试卷分为第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分,共150分,考试时间120分钟.
第Ⅰ卷（选择题,共60分）
注意事项：
1． 答案第Ⅰ卷前,考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上.
2． 每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案,不能答在试题卷上.
3． 考试结束、监考人将本试卷和答题卡一并收回.
一、选择题：本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,选择一个符合题目要求的选项.
1．
等于（ ）
A．2-2i B．2+2i C．-2 D．2
2．在等差数列
中,有
,则此数列的前13项之和为（ ）
A．24 B．39 C．52 D．104
3．下列积分的值等于1的是( )
A. 
B. 
C. 
D. 
4．已知直线
上一点P的横坐标为a,有两个点A（-1,1）,B（3,3）,那么使向量
与
夹角为钝角的一个充分但不必要条件是（ ）
Ａ．-1<a<2 Ｂ．0<a<1 Ｃ．
Ｄ．0<a<2
5．设函数
是定义在
上的以3为周期的奇函数,若
,则a
的取值范围是（ ）
A.
B.
C.
D.
6．在
中,已知sinC=2sin(B+C)cosB,那么一定是（ ）
Ａ．等腰直角三角形 Ｂ．等腰三角形 Ｃ．直角三角形 Ｄ．等边三角形
7．设
是两个不重合的平面,
是两条不同的直线,且
,给出下列命题,其中正确的命题的个数是（ ）
①若
,则
； ②若
,则
；
③若,则； ④若,则.
A .1 B.2 C .3 D. 4
8．已知双曲线
的右支上恰好有两点到O（坐标原点）、F（右焦点）的距离相等,则双曲线的离心率e的取值范围是（ ）
A．1<e
B．e> C．1<e<2 D．e>2
9．已知方程
在区间
之间有一个无理根,若用二分法求出该根并使其精确到0.01,则需要对区间至少进行多少次等分 ( )
A .4 B.6 C .7 D. 8
10．从－3,－2,－1,0,1,2,3,4这8个数中任选3个不同的数组成二次函数y=ax2+bx+c的系数a,b,c则可确定坐标原点在抛物线内部的抛物线有（ ）
A．72条 B．96条 C．128条 D．144条
11．已知是首项为1,公比为
的等比数列,
,
,（其中
表示不超过
的最大整数,如[2.5]=2）．如果数列
为递减的等比数列,那么公比的取值范围是 ( )
A．
B．
C．
D． 
12．下列命题：
①用相关指数R2来刻画回归的效果时，R2的值越大，说明模型拟合的效果越好；
②对分类变量X与Y的随机变量K2的观测值k来说，k越小，“X与Y有关系”可信程度越大；
③两个随机变量相关性越强，则相关系数的绝对值越接近1；
④三维柱形图中柱的高度表示的是各分类变量的频数；其中正确命题的序号是（ ）
A．①②③ B．②③④ C．①③④ D．①②④
第Ⅱ卷（非选择题,共90分）
注意事项：
1．用钢笔或圆珠笔将答案直接写在试卷上.
2．答卷前将密封线内的项目填写清楚.
二、填空题：本大题共6小题,每小题5分,共30分.把答案填在 题中横线上.
13.某学校共有6个年级,现在采用分层抽样的方法从全校3000名学生中抽取一个容量为150的样本进行一项调查. 若该学校高中三年级共有600名学生,则从高中三年级抽取的学生人数应该为 .
14．如果过点（0,1）斜率为k的直线l与圆
交于M、N两点,
且M、N关于直线x+y=0对称,不等式组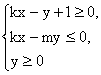
表示的平面区域的面积是______．
15．已知过球面上三点A、B、C的截面到球心的距离等于球半径的一半,且AC=BC=6,AB=4,球的表面积等于__________．
16．设函数f(x)=sin(wx+
)(w＞0,－
＜＜
,给出以下四个结论：
①它的周期为π;
②它的图象关于直线x=
对称；
③它的图象关于点（
,0）对称； ④在区间（－
,0）上是增函数.
以其中两个论断为条件,另两个论断作结论写出你认为正确的一个命题：_ _ __．
（注：填上你认为是正确的一种答案即可）
三、解答题：本大题共6小题,共74分.解答应写出文字说明、证明过程或演算步骤.
17（本小题满分12分）已知函数f(x)=Asin(wx＋j) (x∈R, A>0, w>0, j < )的部分图象如图所示,
(1)试确定f(x)的解析式;
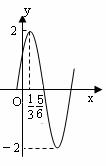(2)若f() = , 求cos( －a)的值
18（本小题满分12分）
有A、B、C、D四个城市，它们都有一个著名的旅游点，依次记为
把A、B、C、D和
分别写成左右两列，现在一名旅游爱好者随机用4条线把左右两边的字母全部连接起来，构成“一一对应”.已知每连对一个得2分，连错得0分.
（1）求该爱好者得分的分布列； （2）求该爱好者得分的数学期望；
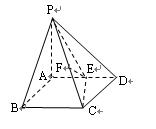19（本小题满分12分）如图, 在四棱锥P－ABCD中,PA⊥平面ABCD, 底面ABCD为正方形, 且PA=AD=2, E、F分别为棱AD、PC的中点.
(1)求异面直线EF和PB所成角的大小;
(2)求证: 平面PCE⊥平面PBC;
(3)求二面角E－PC－D的大小.
20（本小题满分12分）
已知函数
（1） 求函数的单调区间；
（2） 若在区间
上，函数的图象在函数
的下方，求
的取值范围.
21.（本小题满分12分）已知三点
,
其中a为大于零的常数, t为参数, 平面内动点M满足: 
, 且
（1）求动点M的轨迹方程;
(2)若动点M的轨迹在x轴上方的部分与圆心在C
,半径为4的圆相交两点S、T,
求证: C落在以S、T为焦点过F的椭圆上.
22.（本小题满分14分）
已知数列的前
项和为
,对任何正整数
点
都在函数
的图象上，且过点的切线的斜率为
（1）求数列
的通项公式；
（2）若
,求数列
的前项和
;
（3）设
等差数列
的任一项
其中
是
中的最小数，且
求的通项公式.
枣庄市2007届高三模拟考试
理科数学试题(一)参考答案
一、选择题（每小题5分,共60分） DCCBD BBDDD BC
二、填空题（每小题4分,共16分）
13. 30 14. 0.25 15. 54π 16. ①②
③④（或①③②④）
三、解答题：本大题共6小题,共74分.解答应写出文字说明、证明过程或演算步骤.
17.解: (1)由图象可知A=2, = － = , ∴T=2, ω= =π………………………3分
将点(, 2)代入y=2sin(πx＋j), 得 sin(＋j)=1, 又j <
, 所以j = . 故所求解析式为f(x)=2sin(πx＋) (x∈R)………………………………6分
(2)∵f() = , ∴2sin(＋) = , 即, sin(＋) = ………………………………8分
∴cos( －a)=cos[π－2(＋)] =－cos2(＋)=2sin2(＋)－1 =－…………12分
18．解:(I)设连对的个数为
得分为
,则
因此的所有可能的取值为
…………………………………………………………………………………1分
………………………………………………………………………………………………9分
|
| 0 | 2 | 4 | 8 |
|
|
|
|
|
|
所以的分布列为
…………………………………………………………………………………………………10分
（II）
……………………………………………12分
答：该爱好者得分的数学期望为2。
19．解: 以A为坐标原点，直线AB为x轴,直线AD为y轴,直线AP为z轴，建立空间直角坐标系,如图,则A(0,0,0), B(2,0,0),C(2,2,0),D(0,2,0),P(0,0,2).
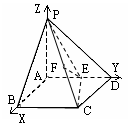(1)∵E为AD的中点, ∴E(0,1,0), 又F为PC的中点,
∴ F(1,1,1).∴
=(1,0,1)
又
=(2,0,－2), ∴cos<,> = =0,
∴<,> = 90°。
异面直线EF和PB所成角的大小为90°. …………………………………………………4分
(2)由(1)知EF⊥PB, 又∵
=(0,2,0), =(1,0,1) ∴·=0, ∴EF⊥BC……6分
∴ EF⊥平面PBC 又EFÌ平面PCE, ∴平面PCE⊥平面PBC…………………8分
(3)过点D作DH⊥PC于H, 在Rt△PDC中, PD=2, DC=2, PC=2, 则CH= , PH:HC=2:1, 又P(0,0,2),C(2,2,0),∴H(,,) ∴
=(,－,), 又=(1,0,1)，
cos<, >= = ∴ <, >= 30°,
∴二面角E－PC－D的大小为30°………………………………………………………12分
20．（1）设投资x万元,A产品利润f(x)万元,B产品利润为g(x)万元
则f(x)=k1x g(x)=k2, 由图1知f(1)= , ∴k1= ,
g(4)=1.6 ∴k2= .…………………………………………………………………4分
故 f(x)= x (x≥0) g(x)= (x≥0) …………………………………………6分
(2)设A产品投入x万元,B产品投入10－x万元．
总利润y万元,则y=x+, (o≤x≤10) ………………………………8分
令t=, (0≤t≤) 则y=＋t＝―(t―2)2＋．…………10分
∴当t＝2时,ymox＝2.8(万元)此时x＝6,故A投入6万元．B投入4万元．…12分
可获得最大利润2.8万元．
21．解:（1）设M
, 
, 
,
A、P点的横坐标相同, 
x轴 
∥x轴或与x轴重合. 
点M到直线x
与M到点F的距离相等, ………………………………………4分
点M的轨迹为以F为焦点,以x为准线的抛物线,
∴动点M的轨迹方程为
……………………………5分
（2）设S(
)、T(
)由题设得圆方程为
……6分
由方程组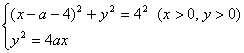
消去y整理得
, ∴
. ……………8分
设S、T到抛物线准线x的距离分别为d1、d2. S、T在抛物线上,
(定值) ………………10分
又
, 
在椭圆上. ………………………………………12分
22．解：（1）
点都在函数的图象上，
………………………………………………………………2分
当
当
（★）
当
也满足（★）式。
数列的通项公式为
………………………………………………4分
（2）由
过点的切线的斜率为
①
由①
4得：
②
由①－②得
……………………………………………………9分
（3）
中的最小数，
的公差是4的倍数，
……………………11分
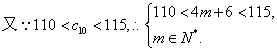解得
设等差数列
的通项公式为
……14分