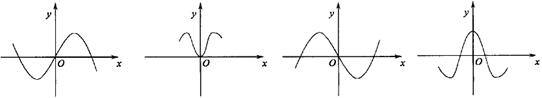枣庄市2007届高三模拟考试
理科数学试题(三)
本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试时间120分钟.
第Ⅰ卷(选择题,共60分)
注意事项:
1. 答第Ⅰ卷前,考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上.
2. 每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案,不能答在试题卷上.
3. 考试结束、监考人将本试卷和答题卡一并收回.
参考公式:
如果事件A、B互斥,那么P(A+B)=P(A)+P(B).
如果事件A、B相互独立,那么P(A+B)=P(A)·P(B).
球的表面积公式![]() ,其中
,其中![]() 表示球的半径.
表示球的半径.
球的体积公式![]() ,其中
,其中![]() 表示球的半径.
表示球的半径.
锥体的体积公式![]() ,其中S表示底面积,
,其中S表示底面积,![]() 表示锥体的高.
表示锥体的高.
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,选择一个符合题目要求的选项.
1.设P、Q是两个非空集合,定义集合间的一种运算“⊙”:P⊙Q=![]()
如果![]() ,则P⊙Q=(
)
,则P⊙Q=(
)
A.![]() B.
B.![]()
C.[1,2] D.(2,+![]() )
)
2. 设向量![]() 与
与![]() 的夹角为
的夹角为![]() ,
,![]() =(2,1),3
=(2,1),3![]() +
+![]() =(5,4),则
=(5,4),则![]() =( )
=( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3. 从2007名学生中选取50名学生参加全国数学联赛,若采用下面的方法选取:先用简单随机抽样从2007
人中剔除7人,剩下的2000人再按系统抽样的方法抽取,则每人入选的概率( )
A.不全相等 B.均不相等
C.都相等,且为![]() D.都相等,且为
D.都相等,且为![]()
4. 设M是![]() m、n、p分别是
m、n、p分别是![]() 的最小值是( )
的最小值是( )
A.8 B.9 C.16 D.18
5. 设曲线y=x2+1在其任一点(x,y)处的切线的斜率为g(x) ,则函数y=g(x)cosx的部分图
象可以为 ( )
|
A. B. C. D.
6. 在等差数列![]() 为一个确定的常数,则其前n项和
为一个确定的常数,则其前n项和![]() 中,也为确定常数
中,也为确定常数
的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7. ![]() 的展开式中含x的正整数指数幂的项数是 ( )
的展开式中含x的正整数指数幂的项数是 ( )
A.0 B.2 C.4 D.6
8. P是双曲线![]() 的右支上一点,F1,F2分别为双曲线的左、右焦点,焦距为2c,则△PF1F2的内切圆的圆心横坐标为( )
的右支上一点,F1,F2分别为双曲线的左、右焦点,焦距为2c,则△PF1F2的内切圆的圆心横坐标为( )
A.b B.a C. c-a D.c-b
9. “a+b=2”是“直线x+y=0与圆(x-a)2+(y-b)2=2相切”的( )
A.充分不必要条件B.必要不充分条件C.充分必要条件 D.既不充分也不必要条件
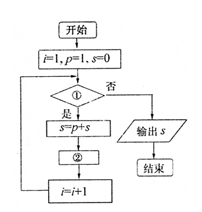 10. 给出30个数:1,2,4,7,11,……其规律是
10. 给出30个数:1,2,4,7,11,……其规律是
第一个数是1,
第二数比第一个数大1,
第三个数比第二个数大2,
第四个数比第三个数大3,……
以此类推,要计算这30个数的和,现已给出了该问题
的程序框图如右图所示,那么框图中判断框①处和执行
框②处应分别填入( )
A.i≤30?;p = p + i-1
B.i≤29?;p = p + i + 1
C.i≤31?;p = p + i
D.i≤30?;p = p + i
 11. 已知正三棱锥V—ABC的正视图,俯视图如右图所
11. 已知正三棱锥V—ABC的正视图,俯视图如右图所
示,其中VA=4,AC=2![]() ,则该三棱锥的侧视
,则该三棱锥的侧视
图的面积为( )
A.9 B.6
C.3![]() D.
D.![]()
12.已知在平面直角坐标系中O(0,0),M(1,![]() ),N(0,1),Q(2,3),动点P(x,y)满足
),N(0,1),Q(2,3),动点P(x,y)满足
![]() 的最大值为( )
的最大值为( )
A.4 B.5 C.6 D.7
| |
二、填空题:本大题有4小题,每小题4分,共16分. 把答案填在题中横线上.
13. 定义—种运算如下:![]() =ad-bc,则复数
=ad-bc,则复数![]() 的共轭复数是
.
的共轭复数是
.
14. 观察等式:![]() ,
,![]() 和
和
![]() ,…,由此得出以下推广命题不正确的是
.
,…,由此得出以下推广命题不正确的是
.
①![]() ;
;
②![]() ;
;
③![]() ;
;
④![]() .
.
15. 甲、乙两人约定上午7:00至8:00之间到某站乘公共汽车,在这段时间内有3班公共汽车,它们开车
时刻分别为7:20,7:40,8:00,如果他们约定,见车就乘,则甲、乙同乘一车的概率为(假定甲、乙
两人到达车站的时刻是互相不牵连的,且每人在7时到8时的任何时刻到达车站是等可能的) .
16.给定下列结论:
①已知命题![]() :
:![]() ;命题
;命题![]() :
:![]()
则命题“![]() ”是假命题;
”是假命题;
②已知直线![]() :
:![]() ,则
,则![]() ⊥
⊥![]() 的充要条件是
的充要条件是![]() ;
;
③若![]() ,则
,则![]() ;
;
④圆![]() 与直线
与直线![]() 相交,所得弦长为2.
相交,所得弦长为2.
其中正确命题的序号为 (把你认为正确的命题序号都填上).
三、解答题:本大题有6小题,共74分. 解答应写出文字说明,证明过程或演算步骤.
17.(本小题满分12分)已知![]() 是三角形
是三角形![]() 三内角,向量
三内角,向量![]() ,且
,且![]() .
.
(Ⅰ)求角![]() ;
;
(Ⅱ)若![]() ,求
,求![]() 的值.
的值.
18.(本小题满分12分)有混在一起质地均匀且粗细相同的长分别为1m、2m、3m的钢管各3根(每根钢管附有不同的编号),现随意抽取4根(假设各钢管被抽取的可能性是均等的),再将抽取的4根首尾相接焊成笔直的一根.
(Ⅰ)求抽取的4根钢管中恰有2根长度相同的概率;
(Ⅱ)若用![]() 表示新焊成的钢管的长度(焊接误差不计),试求
表示新焊成的钢管的长度(焊接误差不计),试求![]() 的概率分布和数学期望.
的概率分布和数学期望.
19.(本小题满分12分)
|
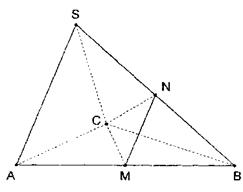
(1)求证:AC⊥SB
(2)求二面角N—CM—B的正切值;
(3)求B的平面CMN的距离.
20.(本小题满分12分)
定义域为D的函数![]() 和
和![]() ,若对于任意的
,若对于任意的![]() 总有
总有![]() 那么称
那么称![]() 可被
可被![]() 替代(通常
替代(通常![]() ≠
≠![]() ).
).
(1)试找出一个可以替代函数![]() 的函数
的函数![]() ,且
,且![]() ≠
≠![]() ;
;
(2)试判断函数![]() 是否可被一次函数
是否可被一次函数![]() 替代,并说明理由.
替代,并说明理由.
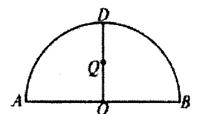
21.(本小题满分12分)如图,ADB为半圆,AB为半圆直径,O为半圆圆心,且OD⊥AB,Q为线段OD的中点,已知AB=4,曲线C过Q点,动点P在曲线C上运动且保持PA+PB的值不变.
(1)建立适当的平面直角坐标系,求曲线C的方程;
(2)过D点的直线![]() 与曲线C相交于不同的两个点M、N,且M在D、N之间,满足
与曲线C相交于不同的两个点M、N,且M在D、N之间,满足![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)过D的直线![]() 与曲线C相交于不同的两点M、N,求△OMN面积的最大值.
与曲线C相交于不同的两点M、N,求△OMN面积的最大值.
|
22.(本小题满分14分)
已知函数![]() 的图象经过点A(2,1)和B(5,2),记
的图象经过点A(2,1)和B(5,2),记![]()
(Ⅰ)求函数![]() 的解析式以及数列
的解析式以及数列![]() 的通项公式;
的通项公式;
(Ⅱ)求使不等式![]() 对一切
对一切![]() 均成立的最大实数
均成立的最大实数![]() ;
;
(Ⅲ)在数列![]() 中,对每一个k∈
中,对每一个k∈![]() ,在
,在![]() 与
与![]() 之间插入
之间插入![]() 个
个![]() ,得到新数列
,得到新数列![]() ,设
,设![]() 是数列
是数列![]() 的前
的前![]() 项和,试问是否存在正整数
项和,试问是否存在正整数![]() ,使得
,使得![]() =2007成立.若存在,请求出
=2007成立.若存在,请求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
枣庄市2007届高三模拟考试
理科数学试题(三)参考答案及评分标准
一、选择题(每小题5分,共60分)ADCCA BBBAD BC
二、填空题(每小题4分,共16分)13. -1-3i 14. ① 15.![]() 16 ①③
16 ①③
三、解答题:
17.解:(Ⅰ)∵![]() ,∴
,∴![]() ,
,
∴![]() ,
,
![]() ,
,![]() ,…………………………………………………………3分
,…………………………………………………………3分
∵![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∴![]() ………………………………………………………………………………………………6分
………………………………………………………………………………………………6分
(Ⅱ)∵![]() ,
,
∴由正弦定理得![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,………………………………………9分
,………………………………………9分
即![]() …………………………………………………………………………………12分
…………………………………………………………………………………12分
18.解:(Ⅰ)抽取的4根钢管中恰有2根长度相同的概率为:
![]() .…………………………………………………………………………4分
.…………………………………………………………………………4分
(Ⅱ)新焊接成钢管的长度的可能值有7种,最短的可能值为5m,最长的可能值为11m.
当![]() ,
,
当![]() ,
,
当![]() ,
,
当![]() .………………………………………………8分
.………………………………………………8分
![]() 的分布列为:
的分布列为:
|
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| P |
|
|
|
|
|
|
|
![]() .………………………12分
.………………………12分
19. 解:(1)取AC中点为D,∵![]() ,
,
∴AC⊥平面SDB, ∴AC⊥SB;…………………………………………………………………………3分
(2)取DB中点为E
∵N为SB的中点,∴NE∥SD
又∵平面SAC⊥平面ABC,SD⊥AC,SD在平面SAC内,
∴SD⊥平面ABC,∴NE⊥平面ABC,过E作EF⊥CM于F,
∴NF⊥CM,
∴∠NFE为所求二面角N—CM—B的平面角.…………………………………………………………6分
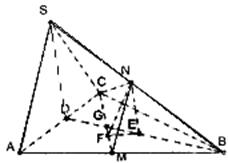 在正三角形ABC中,设中线BD与CM交于G,
在正三角形ABC中,设中线BD与CM交于G,
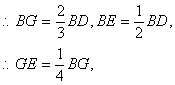
∵CM⊥MB,∴EF//MB,![]()
又SA=SC=![]()
![]()
在三角形NEF中,![]() 所以二面角的正切值为
所以二面角的正切值为![]() .…………………9分
.…………………9分
(3)设B到平面CMN的距离为h,
![]() ,
,
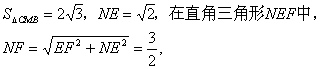
![]() . …………………………………………………12分
. …………………………………………………12分
20.解:(1)由定义解得![]() ,取
,取![]() 即可. …………………………………4分
即可. …………………………………4分
(2)![]() ,
,
令![]() ,则
,则![]() .
.
令![]() ,…………………………………………………………………………………6分
,…………………………………………………………………………………6分
当![]() 上是减数函数;
上是减数函数;
当![]() ,所以
,所以![]() 在(4,6)上是增函数.
在(4,6)上是增函数.
![]() 的极小值是
的极小值是![]() ,…………………………………………………………9分
,…………………………………………………………9分
又![]() ,
,![]() ,
,
![]() ,
,![]()
![]() ……………………………………………………………………………12分
……………………………………………………………………………12分
21.解:(1)以AB、OD所在直线分别为x轴、y轴,O为原点,建立平面直角坐标系.
![]()
∴由线C以原点为中心,A、B为焦点的椭圆,
设其长半轴长为a,短半轴长为b,半焦距为c,
则![]() ∴
∴![]()
∴曲线C的方程为:![]() ………………………………………………………………2分
………………………………………………………………2分
(2)(i)当![]() 与y轴重合时,
与y轴重合时,![]() ………………………………………………………………3分
………………………………………………………………3分
(ii)当![]() 与y轴不重合时,设直线
与y轴不重合时,设直线![]() 的方程为
的方程为![]() ,代入曲线C的方程并整理,得
,代入曲线C的方程并整理,得![]()
设![]() 则
则
|
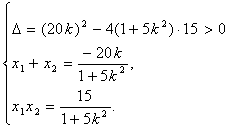
由①得![]() ………………………………………………………………………………………6分
………………………………………………………………………………………6分
又∵![]()
M在D、N之间,故![]() ∴
∴![]() ……………………………………7分
……………………………………7分
由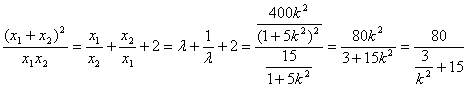
而![]() ∴
∴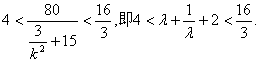 ∴
∴![]()
综上所述,![]() …………………………………………………………………………9分
…………………………………………………………………………9分
(3)点O到直线MN的距离![]()
弦MN的长![]()
∴![]() ,……………………………………………………10分
,……………………………………………………10分
设![]()
∵![]() ∴
∴![]()
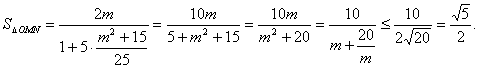
当且仅当![]() 时等号成立.此时
时等号成立.此时![]()
∴△OMN的面积有最大值为![]() …………………………………………………………………12分
…………………………………………………………………12分
22.解:(I)由已知,得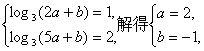 …………………………………………………2分
…………………………………………………2分
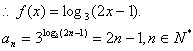
数列![]() 的通项公式为
的通项公式为![]() .……………………………………………………………4分
.……………………………………………………………4分
(II)由题意![]() 对n∈
对n∈![]() 恒成立.
恒成立.
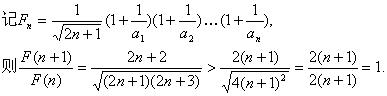
∵![]() ,
,![]() ,
,![]() 随
随![]() 增大而增大.
增大而增大.
∴![]() 的最小值为
的最小值为![]()
![]() .
.
∴![]() ≤
≤![]() ,即
,即![]() 的最大值为
的最大值为![]() .……………………………………………………9分
.……………………………………………………9分
(Ⅲ)∵an=2n-1,∴在数列{bn}中,an及其前面所有项之和为
![]() +
+![]() . …………………………11分
. …………………………11分
显然可得![]()
又![]() 在数列
在数列![]() 中的项数为
中的项数为![]() ,
,![]() 在数列
在数列![]() 中的项数为1034,
中的项数为1034,
![]()
![]() 且
且![]() 不能被
不能被![]() 整除.
整除.
∴满足![]() 的正整数
的正整数![]() 不存在. ……………………………………………………14分
不存在. ……………………………………………………14分