枣庄市2007届高三模拟考试
理科数学试题(二)
本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试时间120分钟.
第Ⅰ卷(选择题,共60分)
注意事项:
1. 答案第Ⅰ卷前,考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上.
2. 每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案,不能答在试题卷上.
3. 考试结束、监考人将本试卷和答题卡一并收回.
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,选择一个符合题目要求的选项.
1. 复数![]() 的共轭复数是(
)
的共轭复数是(
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.已知集合![]() ,则a的值为( )
,则a的值为( )
A.1 B.2 C.1或2 D.不为零的任意实数
3.方程log3x+x=3的解所在的区间为
A.(0,2) B.(1,2) C.(2,3) D.(3,4)
4.已知圆C:![]() ,直线
,直线![]() 圆上存在两点到直线l的距离为1,则k的取值范围是 ( )
圆上存在两点到直线l的距离为1,则k的取值范围是 ( )
A.(-17,-7) B.(3,13)
C.(-17,-7)∪(3,13) D.[-17,-7]∪[3,13]
5.已知![]() 则关于
则关于![]() 的方程有实数根的概率为( )
的方程有实数根的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.已知直线![]() 、
、![]() ,平面
,平面![]() ,则下列命题中是假命题的是
,则下列命题中是假命题的是
A.若![]() ,
,![]() ,则
,则![]() ;
;
B.若![]() ,
,![]() ,则
,则![]() ;
;
C.若![]() ,
,![]() ,则
,则![]() ;
;
D.若![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() .
.
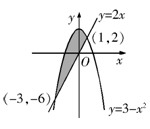 7.如图,阴影部分的面积是( )
7.如图,阴影部分的面积是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.已知二项式![]() 的展开式中不含
的展开式中不含![]() 的项为160,
的项为160,
则![]() 的值为( )
的值为( )
A.-2 B.2 C.![]() D.
D.![]()
9.已知不等式![]() 对任意正实数x,y恒成立,则正实数a的最小值是( )
对任意正实数x,y恒成立,则正实数a的最小值是( )
A.2 B.4 C.6 D.8
10.已知椭圆![]() +y2=1(a>1)的两个焦点为F1、F2,P为椭圆上一点,且∠F1PF2=60°,则PF1·PF2的值为
( )
+y2=1(a>1)的两个焦点为F1、F2,P为椭圆上一点,且∠F1PF2=60°,则PF1·PF2的值为
( )
A.1
B.![]() C.
C.![]() D.
D.![]()
11.若数列{an}的通项公式![]() ,数列{an}的最大项为第x项,最小项为第y项,则x+y等于 ( )
,数列{an}的最大项为第x项,最小项为第y项,则x+y等于 ( )
A.3 B.4 C.5 D.6
12.设奇函数![]() 上是增函数,且
上是增函数,且![]() 对所有的
对所有的![]() 都成立,当
都成立,当![]() 时,则t的取值范围是 ( )
时,则t的取值范围是 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
第Ⅱ卷(非选择题,共90分)
注意事项:
1.用钢笔或圆珠笔将答案直接写在试卷上.
2.答卷前将密封线内的项目填写清楚.
二、填空题:本大题共6小题,每小题5分,共30分.把答案填在题中横线上.
13.若双曲线的渐近线方程为![]() ,它的一个焦点是
,它的一个焦点是![]() ,则双曲线的方程是__________.
,则双曲线的方程是__________.
14.已知一个几何体的主视图及左视图均是边长为2的正三角形,俯视图是直径为2的圆,则此几何体的外接球的表面积为 .
15.已知等差数列{an}的前n项和为Sn,若m>1,m∈N*,且![]() ,则m等于
.
,则m等于
.
16.若判断框内填入![]() 则下面的程序框图输出的结果为
.
则下面的程序框图输出的结果为
.
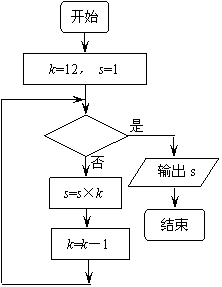
三、解答题:本大题共6小题,共74分.解答应写出文字说明、证明过程或演算步骤.
17.(本题满分12分)
![]() 、
、![]() 、
、![]() 为
为![]() 的三内角,且其对边分别为
的三内角,且其对边分别为![]() 、
、![]() 、
、![]() .
.
若![]() =
=![]() ,
,![]() =
=![]() ,且
,且![]() .
.
(1)求![]() ;
;
(2)若![]() =
=![]() ,三角形面积
,三角形面积![]() =
=![]() ,求
,求![]() 的值.
的值.
18.(本题满分12分)
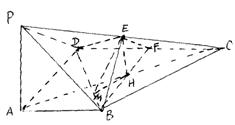
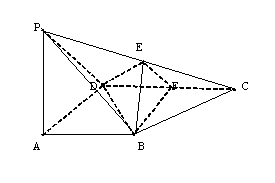 如图,在四棱锥P—ABCD中,PA⊥底面ABCD,
如图,在四棱锥P—ABCD中,PA⊥底面ABCD,
∠![]() , AB∥CD,AD=CD=2AB=2,E、
, AB∥CD,AD=CD=2AB=2,E、
F分别是PC、CD的中点
(Ⅰ)证明:CD⊥平面BEF
(Ⅱ)设![]() ,
,
求K的值.
19.(本题满分12分)
设各项为正数的等比数列![]() 的首项
的首项![]() ,前n项和为
,前n项和为![]() ,且
,且![]() .
.
(1)求![]() 的通项;(2)求
的通项;(2)求![]() 的前n项和
的前n项和![]() .
.
20.(本题满分12分)
在一个盒子中,放有标号分别为![]() ,
,![]() ,
,![]() 的三张卡片,现从这个盒子中,有放回地先后抽得两张卡片的标号分别为
的三张卡片,现从这个盒子中,有放回地先后抽得两张卡片的标号分别为![]() 、
、![]() ,记
,记![]() .
.
(1)求随机变量![]() 的最大值,并求事件“
的最大值,并求事件“![]() 取得最大值”的概率;
取得最大值”的概率;
(2)求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
21.(本题满分12分)
已知函数![]()
(1)求函数![]() 的单调区间;
的单调区间;
(2)当![]() 时,试确定
时,试确定![]() 的取值范围,使函数
的取值范围,使函数![]() 的图象在函数
的图象在函数![]() 图象的下方,并证明你的结论.
图象的下方,并证明你的结论.
22. (本小题满分14分)
已知点H(-3,0),点P在![]() 轴上,点Q在
轴上,点Q在![]() 轴的正半轴上,点M在直线PQ上,且满足
轴的正半轴上,点M在直线PQ上,且满足![]() ,
, ![]()
![]() .
.
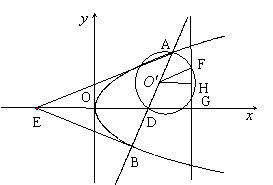
(1)当点P在![]() 轴上移动时,求点M的轨迹C;
轴上移动时,求点M的轨迹C;
(2)过定点![]() 作直线
作直线![]() 交轨迹C于A、B两点,E是D点关于坐标原点O的对称点,求证:
交轨迹C于A、B两点,E是D点关于坐标原点O的对称点,求证:![]() ;
;
 (3)在(Ⅱ)中,是否存在垂直于
(3)在(Ⅱ)中,是否存在垂直于![]() 轴的直线
轴的直线![]() 被以AD为直径的圆截得的弦长恒为定值?若存在求出
被以AD为直径的圆截得的弦长恒为定值?若存在求出![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
枣庄市2007届高三模拟考试
理科数学试题(二)参考答案及评分标准
一、选择题(每小题5分,共60分) B DCCB CCABC A C
二、填空题(每小题4分,共16分)13.![]() 14.
14.![]() 15.10 16.132
15.10 16.132
三、解答题:
17.解:(1)∵![]() =
=![]() ,
,![]() =
=![]() ,且
,且![]() ,
,
∴ ![]() , ………………………………………2分
, ………………………………………2分
∴ ![]() ,…………………………………………………………3分
,…………………………………………………………3分
即 ![]() ………………………………………………………4分
………………………………………………………4分
即-![]() ,又
,又![]() ,∴
,∴![]() .………………………………6分
.………………………………6分
(2)![]()
![]() ,∴
,∴![]() . …………………8分
. …………………8分
又由余弦定理得:![]() .…………10分
.…………10分
∴16=![]() ,故
,故![]() .……………………………………………12分
.……………………………………………12分
![]() 18.解: (Ⅰ)证明:
18.解: (Ⅰ)证明: 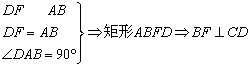
DA⊥平面ABCD,AD⊥CD ………………3分
![]()
 ………5分
………5分
∴ CD⊥平面BEF ……………6分
(Ⅱ)连结AC且交BF于H,可知H是AC中点,连结EH
由E是PC中点得EH∥PA PA⊥平面ABCD
得EH⊥平面ABCD,且EH![]() ……………8分
……………8分
作HM⊥BD于M,连结EM,由三垂线定理可得EM⊥BD
故∠EMH为二面角E—BD—F的平面角,故∠EMH=60……………10分
∵ Rt△HBM∽Rt△DBF
故![]()
得![]() 得
得![]()
在Rt△EHM中,![]() ……………12分
……………12分
19.解:(1)由 ![]() 得
得 ![]()
即![]()
可得![]() …………………………4分
…………………………4分
因为![]() ,所以
,所以 ![]() 解得
解得![]() ,因而
,因而 ![]()
……………………………………………………………………………………………6分
(2)因为![]() 是首项
是首项![]() 、公比
、公比![]() 的等比数列,故
的等比数列,故
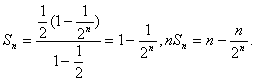
则数列![]() 的前n项和
的前n项和 ![]()
![]()
前两式相减,得 ![]()
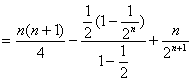 即
即 ![]()
……………………………………………………………………………………………12分
20.解:(1)![]() 、
、![]() 可能的取值为
可能的取值为![]() 、
、![]() 、
、![]() ,
,
![]() ,
,![]() ,
,
![]() ,且当
,且当![]() 或
或![]() 时,
时,![]() .……………………………3分
.……………………………3分
因此,随机变量![]() 的最大值为
的最大值为![]() .
.
![]() 有放回抽两张卡片的所有情况有
有放回抽两张卡片的所有情况有![]() 种,
种,
![]() .
.
答:随机变量![]() 的最大值为
的最大值为![]() ,事件“
,事件“![]() 取得最大值”的概率为
取得最大值”的概率为![]() . ………5分
. ………5分
(2)![]() 的所有取值为
的所有取值为![]() .
.
![]() 时,只有
时,只有![]() 这一种情况,
这一种情况,
![]() 时,有
时,有![]() 或
或![]() 或
或![]() 或
或![]() 四种情况,
四种情况,
![]() 时,有
时,有![]() 或
或![]() 两种情况.
两种情况.
![]() ,
,![]() ,
,![]() .………………………………10分
.………………………………10分
则随机变量![]() 的分布列为:
的分布列为:
|
|
|
|
|
|
|
|
|
|
|
|
因此,数学期望![]() .………………………12分
.………………………12分
21.解:(1)![]() …………2分
…………2分
(i)当![]() 时,函数定义域为
时,函数定义域为![]()
![]() ………………………………………………4分
………………………………………………4分
(ii)当![]() 时,函数定义域为
时,函数定义域为![]()
于是由![]() 得
得![]()
由![]() 得
得![]()
所以当![]() 时,函数的增区间为
时,函数的增区间为![]() 减区间为
减区间为![]() ……………7分
……………7分
(2)构造函数![]()
则![]() ………………………………………10分
………………………………………10分
![]() 当
当![]() 时,
时,![]() 当
当![]() 时,
时,![]() 当
当![]() 时,
时,![]()
所以![]() 在
在![]() 上为减函数,在
上为减函数,在![]() 上为增函数.
上为增函数.
![]()
所以当![]() 时,函数
时,函数![]() 的图象在函数
的图象在函数![]() 图象的下方.
图象的下方.
22.解:(1)设![]()
![]()
![]()
![]() 且
且![]() …………………2分
…………………2分
![]() …………………3分
…………………3分
![]() ………………………………………………4分
………………………………………………4分
∴动点M的轨迹C是以O(0,0)为顶点,以(1,0)为焦点的抛物线(除去原点).
…………………………………………5分
(2)解法一:(1)当直线![]() 垂直于
垂直于![]() 轴时,根据抛物线的对称性,有
轴时,根据抛物线的对称性,有![]() ;
;
……………6分
 当直线
当直线![]() 与
与![]() 轴不垂直时,依题意,可设直线
轴不垂直时,依题意,可设直线![]() 的方程为
的方程为![]() ,
,![]() ,则A,B两点的坐标满足方程组
,则A,B两点的坐标满足方程组
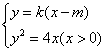
消去![]() 并整理,得
并整理,得
![]() .
.
![]() ……………7分
……………7分
设直线AE和BE的斜率分别为![]() ,则
,则
![]() =
=![]()
![]()
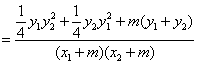
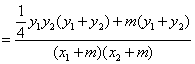
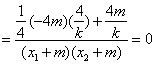 …………………9分
…………………9分
![]()
![]()
![]() ,
,![]()
![]() .
.
综合(1)、(2)可知![]() . …………………………………………10分
. …………………………………………10分
 解法二:依题意,设直线
解法二:依题意,设直线![]() 的方程为
的方程为![]() ,
,![]() ,则A,B两点的坐标满足方程组
,则A,B两点的坐标满足方程组
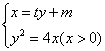
消去![]() 并整理,得
并整理,得
![]()
![]() ……………7分
……………7分
设直线AE和BE的斜率分别为![]() ,则
,则
![]() =
=![]()
![]()
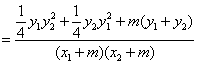
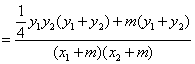
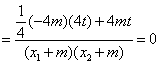 …………………………9分
…………………………9分
![]()
![]()
![]() ,
,![]()
![]() .……………………………………………………………………10分
.……………………………………………………………………10分
(3)假设存在满足条件的直线![]() ,其方程为
,其方程为![]() ,AD的中点为
,AD的中点为![]() ,
,![]() 与AD为直径的圆相交于点F、G,FG的中点为H,则
与AD为直径的圆相交于点F、G,FG的中点为H,则![]() ,
,![]() 点的坐标为
点的坐标为![]() .
.
![]()
![]()
![]()
![]()
![]()
![]() .……………………………………………………12分
.……………………………………………………12分
![]()
令![]() ,得
,得![]()
此时,![]()
∴当![]() ,即
,即![]() 时,
时,![]() (定值)
(定值)
∴当![]() 时,满足条件的直线
时,满足条件的直线![]() 存在,其方程为
存在,其方程为![]() ;当
;当![]() 时,满足条件的直线
时,满足条件的直线![]() 不存在. …………………………………………… …………………………14分
不存在. …………………………………………… …………………………14分