钦州市大寺中学2007届高三毕业班模拟练习(1)
文科数学
一.选择题(每小题5分,共60分)
1.已知不等式![]() 的解集为A,函数
的解集为A,函数![]() 的定义或为B,则
的定义或为B,则![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.将函数![]() 的图象按向量a平移后,得到
的图象按向量a平移后,得到![]() 的图象,则
的图象,则
A.a=(1,2) B.a=(1,-2) C.a=(-1,2) D.a=(-1,-2)
3. 在![]() 的展开式中
的展开式中![]() 的系数是
的系数是
A.240 B.160 C.-160 D.-240
4.已知函数![]() , 则
, 则![]() 与
与![]() 的大小关系是
的大小关系是
A、![]() B、
B、![]() C、
C、![]() D、不能确定
D、不能确定
5.在![]() 中,若
中,若![]() 的形状一定是
的形状一定是
A.等腰直角三角形 B.等边三角形
C.直角三角形 D.等腰三角形
6.某班上午要上语文、数学、英语、体育各一节,体育课既不在第一节也不在第四节,共有不同的排法数为( )
A.12 B.20 C.22 D.24
7.数列![]() 中,已知对任意正整数
中,已知对任意正整数![]() ,
,![]() ,则
,则![]() 等于( )
等于( )
A.(2n-1)2 B.![]() (2n-1) C.
(2n-1) C.![]() (4n-1) D.4n-1
(4n-1) D.4n-1
8.设双曲线![]() 的两条渐近线与右准线的三角形区域(包含边界)为D,P(x,y)为D内一个动点,则目标函数
的两条渐近线与右准线的三角形区域(包含边界)为D,P(x,y)为D内一个动点,则目标函数![]() 的最小值为
的最小值为
A.-2 B.![]() C.0 D.
C.0 D.![]()
9.一个与球心距离为1的平面截球体所得的圆面面积为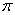 ,则球的体积为
,则球的体积为
A. 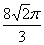 B.
B.
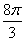 C.
C.
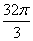 D.
8
D.
8
10.设m,n是两条不同的直线,α、β是两个不同的平面,考查下列命题,其中正确的命题是( )
A.m⊥α,n![]() β,m⊥n
β,m⊥n![]() α⊥β
B.α∥β,m⊥α,n∥β
α⊥β
B.α∥β,m⊥α,n∥β![]() m⊥n
m⊥n
C.α⊥β,m⊥α,n∥β![]() m⊥n
D.α⊥β,α∩β=m,m⊥n
m⊥n
D.α⊥β,α∩β=m,m⊥n![]() n⊥β
n⊥β
11.已知定义在R上的奇函数f(x)在区间(0,+∞)上是增函数,若![]() ,△ABC的内角A满足f(cosA)<0
则A的取值范围
,△ABC的内角A满足f(cosA)<0
则A的取值范围
A.![]() B.
B.![]() C.
C.![]() D.
D. ![]()
12.A,B两位同学各有3张卡片,现以投掷均匀硬币的形式进行游戏,当出现下面向上时A赢得B一张卡片,否则B赢得A一张卡片。如果某人已赢得所有卡片,则游戏终止。那么恰好掷完5次硬币时游戏终止的概率是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二.填空题(每小题4分,共16分)
13.若tanx=2,则![]() ________________
________________
14.抛物线![]() 的焦点坐标是
.
的焦点坐标是
.
15.设(3x-1)n=a0+a1x+a2x2+…+anxn,已知a0+a1+a2+…+an=128,则a2=
16.定义在(-1,1)上的函数![]() 时函数
时函数![]() 的导函数
的导函数![]() 的取值范围为
.
的取值范围为
.
三.解答题(第17、18、19、20、21题每题12分,第22题14分,共74分)
17.已知集合![]()
| |
|
18.在一次语文测试中,有一道把我国四大文学名著《水浒传》、《三国演义》、《西游记》、《红楼梦》与它们的作者连线题,已知连对一个得3分,连错一个不得分,一位同学该题得![]() 分.
分.
(1)该同学恰好得3分的概率;(2)该同学得分不少于6分的概率.
.
19.在△ABC中,∠A、∠B、∠C的对边的边长分别为a、b、c,且a,b,c成等比数列.
(1)求角B的取值范围;
(2)若关于角B的不等式![]() 恒成立,求m的取值范围.
恒成立,求m的取值范围.
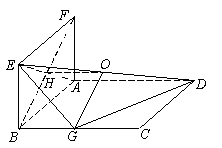
20.如图, 正方形ABCD和ABEF的边长均为1,且它们所在的平面互相垂直,G为BC的中点.
(Ⅰ)求点G到平面ADE的距离;
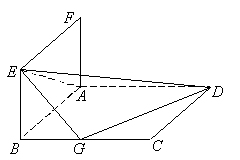 (Ⅱ)求直线AD与平面DEG所成的角;
(Ⅱ)求直线AD与平面DEG所成的角;
21.已知等比数列![]() 中,
中,![]() .若
.若![]() ,数列
,数列![]() 前
前![]() 项的和为
项的和为![]() .
.
(Ⅰ)若![]() ,求
,求![]() 的值;(Ⅱ)求不等式
的值;(Ⅱ)求不等式![]() 的解集.
的解集.
22.设![]() ,定点F(a,0),直线l :x=-a交x轴于点H,点B是l上的动点,过点B垂直于l的直线与线段BF的垂直平分线交于点M.
,定点F(a,0),直线l :x=-a交x轴于点H,点B是l上的动点,过点B垂直于l的直线与线段BF的垂直平分线交于点M.
(I)求点M的轨迹C的方程;
(II)设直线BF与曲线C交于P,Q两点,证明:向量![]() 、
、![]() 与
与![]() 的夹角相等.
的夹角相等.
钦州市大寺中学2007届高三数学[文科]模拟练习(1)
参考答案
一.选择题
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | A | C | C | B | D | A | C | B | A | B | D | D |
二.填空题
13.![]() ;14.
;14.![]() ;15.-189;16.
;15.-189;16.![]() 。
。
三.解答题
17..解:(Ⅰ)因为![]() 所以
所以![]()
![]() ……3分
……3分
|
所以( ![]()
…………………………………………………………………………6分
|
| |
| |
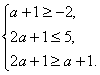
解得![]() ……………………………………………………………11分
……………………………………………………………11分
解得![]() 即实数a的取值范围是[0,2].…………………………12分
即实数a的取值范围是[0,2].…………………………12分
18.(1)该同学恰好得3分的概率为![]()
(2)![]() ,
,![]()
该同学得分不少于6分的概率为![]() ………
………![]()
19.(1)![]()
当且仅当a=b=c时,![]()
![]() …………………………5分
…………………………5分
(2)![]()
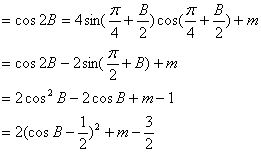
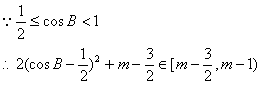
∵不等式![]() 恒成立,
恒成立,
![]() ,故m的取值范围为
,故m的取值范围为![]() …………………………………12分
…………………………………12分
20.(Ⅰ)∵BC∥AD, AD![]() 面ADE,
面ADE,
∴点G到平面ADE的距离即点B到平面ADE的距离.
连BF交AE于H,则BF⊥AE,又BF⊥AD.
 ∴BH即点B到平面ADE的距离.………………………(2分)
∴BH即点B到平面ADE的距离.………………………(2分)
在Rt△ABE中,![]() .
.
∴点G到平面ADE的距离为![]() .…(4分)
.…(4分)
(Ⅱ)设DE中点为O,连OG, OH,
则OH ![]()
![]() AD,BG
AD,BG ![]()
![]() AD.
AD.
∴四边形BHOG为平行四边形.………………………(6分)
∴GO∥BH.
由(Ⅰ)BH⊥面ADE,∴GO⊥面ADE.………………………(8分)
又GO![]() 面DEG.∴面DEG⊥面ADE.
面DEG.∴面DEG⊥面ADE.
∴过点A作AM⊥DE于M,则AM⊥面DEG.
∴![]() 为直线AD与平面DEG所成的角.………………………(10分)
为直线AD与平面DEG所成的角.………………………(10分)
在Rt△ADE中,![]() .∴
.∴![]() .
.
∴直线AD与平面DEG所成的角为![]() .………………………(12分)
.………………………(12分)
21.(Ⅰ)![]() 得
得![]()
![]()
![]()
![]()
![]()
![]() 是以
是以![]() 为首项,2为公差的等差数列.
为首项,2为公差的等差数列.
![]()
![]() ┅┅┅┅┅┅┅┅8分
┅┅┅┅┅┅┅┅8分
(Ⅱ)![]()
![]()
![]()
![]() 即,所求不等式的解集为
即,所求不等式的解集为![]() ┅┅┅┅┅┅┅┅12分
┅┅┅┅┅┅┅┅12分
22.
(I)解:连接MF,依题意有MF=MB,…………………………………………3分
所以动点M的轨迹是以F(![]() ,0)为焦点,直线l: x=-
,0)为焦点,直线l: x=-![]() 为准线的抛物线,
为准线的抛物线,
所以C的方程为![]() ………………………………………………5分
………………………………………………5分
(II)解:设P,Q的坐标分别为![]()
依题意直线BF的斜率存在且不为0,设直线BF的方程为![]()
将其与C的方程联立,消去y得
![]() ……………………8分
……………………8分
故![]()
记向量![]()
因为![]()
所以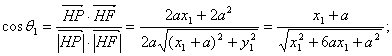 ……11分
……11分
同理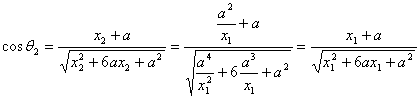
因为![]()
所以![]() 即向量
即向量![]() 、
、![]() 与
与![]() 的夹角相等。……………………14分
的夹角相等。……………………14分